
FUNCIÓN TRIGONOMÉTRICA INVERSA Por Julia
Ángela Ramón Ortiz Desde que Descartes y Newton
idearon el sistema de coordenadas cartesianas para relacionar
expresiones algebraícas y geométricas, la
trigonometría ha adoptado esta herramienta para enfocar
ade manera más asequible su teoría a partir de
puntos en la circunferencia unitaria en el plano cartesiano.
Siendo el método de coordenadas desarrollado por Descartes
(1596-1650) para ubicar un punto del plano fue fundamental para
la evolución del concepto de función
trigonométrica, que se sonstituye en una de las bases para
que Isaac Newton inventara el cálculo diferencial e
integral, sustentada en la representación de muchas
funciones matemáticas utilizando series infinitas de
potencias de la variable x. Desarrollando series para el sen(x),
cos(x) y la tan(x); que hoy desempeñan un importante papel
tanto en las matemáticas puras como en las aplicadas. En
el siglo XVIII, el físico y matemático suizo
Leonhard Euler, explicó que las propiedades de la
trigonometría eran consecuencia de la aritmética de
los números complejos. Estudió además la
notación actual de las funciones trigonométricas y
se le atribuye el descubrimiento de la letra e como base del
logaritmo natural, así como la unidad imaginaria que
generalmente se denota con la letra i. Euler también
popularizó el número pi (p). Durante el siglo XX la
trigonometría ha realizado muchos aportes en el estudio de
los fenómenos de onda y oscilatorio, así como el
comportamiento periódico, el cual se relaciona con las
propiedades analíticas de las funciones
trigonométricas. En astronomía se utiliza para
medir distancias a estrellas próximas, para la
medición de distancias entre puntos geográficos, y
en sistemas de navegación satelital; así como el
desarrollo de la informática, las telecomunicaciones y la
comprensión de diversos fenómenos
periódicos. De lo mencionado líneas arriba, en este
estudio se hace un breve resumen de las funciones
trigonométricas inversas apartir de las respectivas
funciones trigonométricas que por su esencia
períodica se hace necesario algunas restricciones de sus
dominios para un estudio pertinente de sus funciones
inversas.

? Ángela Ramón Ortiz FUNCIONES
TRIGONOMÉTRICAS INVERSAS Y P(?4 , 3) Si P = (?4 , 3).
¿Cuánto mide el radio vector? cos(?) = …….? ? =
….. O X sen(?) = …….? ? = ….. cot(?) = ….. ? ? = …..
tan(?) = …….? ? = ….. OBJETIVO: Al término del
estudio de esta unidad estará en condiciones de:
DETERMINAR LAS FUNCIONES TRIGONOMÉTRICAS INVERSAS,
IDENTIFICANDO SUS DOMINIOS Y RANGOS, GRÁFICOS Y SUS
APLICACIONES EN LA RESOLUCIÓN DE ECUACIONES
TRIGONOMÉTRICAS. 2

Funciones trigonométricas inversas REQUISITOS ¡Para
abordar el estudio de esta unidad es preciso que conozcas! 1.
Funciones trigonométricas seno, coseno y tangente. 2.
Gráfica y algunas propiedades de las funciones seno,
coseno y tangente. 3. Funciones inyectivas y crecientes. 4.
Inversa de funciones reales de variable real. 5.
Composición de funciones reales de variable real inversas.
6. Gráfica de las funciones inversas. OBJETIVOS
¿Qué lograremos en esta unidad? 1. Identificar
gráficamente funciones invertibles. 2. Definir la
función arco coseno, trazar su gráfica e
identificar propiedades. 3. Definir la función arco seno,
trazar su gráfica e identificar propiedades. 4. Definir la
función arco tangente, trazar su gráfica e
identificar propiedades. 5. Identificar las inversas de las
funciones cotangente, secante y cosecante, trazando sus
gráficas correspondientes. CONTENIDOS ¿Qué
aprenderemos a través de esta unidad? 4.1. Función
inversa 4.2. Función inversa del Seno 4.3. Función
inversa del Coseno 4.4. Función inversa de la Tangente
4.5. Función inversa de la cotangente, secante y
cosecante. 3

y ? 1 y 1 y 1 y 1 Y de y x = – Ángela Ramón
Ortiz DESARROLLO EXPLORACIÓN-MOTIVACIÓN–
PROBLEMATIZACIÓN TEMA 1: Despejar la variable
independiente en función de la dependiente. 1) Dado la
función y = 3x + 1, para despejar x en términos de
y, se transponen al primer miembro el término
independiente 1, luego el factor 3; es decir de y = 3x + 1, se
tiene y – 1 = 3x, luego: ? x , o sea: x ? ? . Aquí
resulta que x 3 3 3 es función de y, dado por x = g(y) = ?
para y ? R, luego y = 3x + 1 equivale 3 3 a x ? ? . Además
y = 3x + 1, para x? R es una función inyectiva. 3 3
Gráficamente: y =3x+1, x? R L: y=x y =x/3 – 1/3, x?
R X Figura 1 2) Dado la función y = x2 + 1, al despejar x
en términos de y, se tiene: De y = x2 + 1, y – 1 =
x2 o sea x ? y ? 1 , que está definido para y – 1 ?
0, o sea y ? 1. Por definición valor absoluto, resulta: x
= y ? 1 ó x = – y ? 1 ; que definen dos funciones: x
= y ? 1 = g(y) y ? 1 = h(y), como x ? R, la función y = x2
+1, no es inyectiva. 4

Funciones trigonométricas inversas Pero si consideramos x
? 0: la función y = x2 + 1, equivale a x = inyectiva.
Análogamente, si x ? 0, la función y = x2 + 1,
equivale a x = – inyectiva. y ? 1 y es y ? 1 y es O Y y
=x2+1 x? R y =1 X Y y =x2+1 x ? 0 y =x2+1 x ? 0 Y O X O O X
Figura 2 5
? Y Ángela Ramón Ortiz 1. FUNCIÓN INVERSA
Dada la función y = f (x), con dominio A ? R y rango B ?
R, e inyectiva al despejar x de y = f (x) resulta x = g(y),
intercambiando x e y, se tiene: y = g(x) para x ? B e y ? A, se
llama función inversa de f y se denota por f 1. Luego: y =
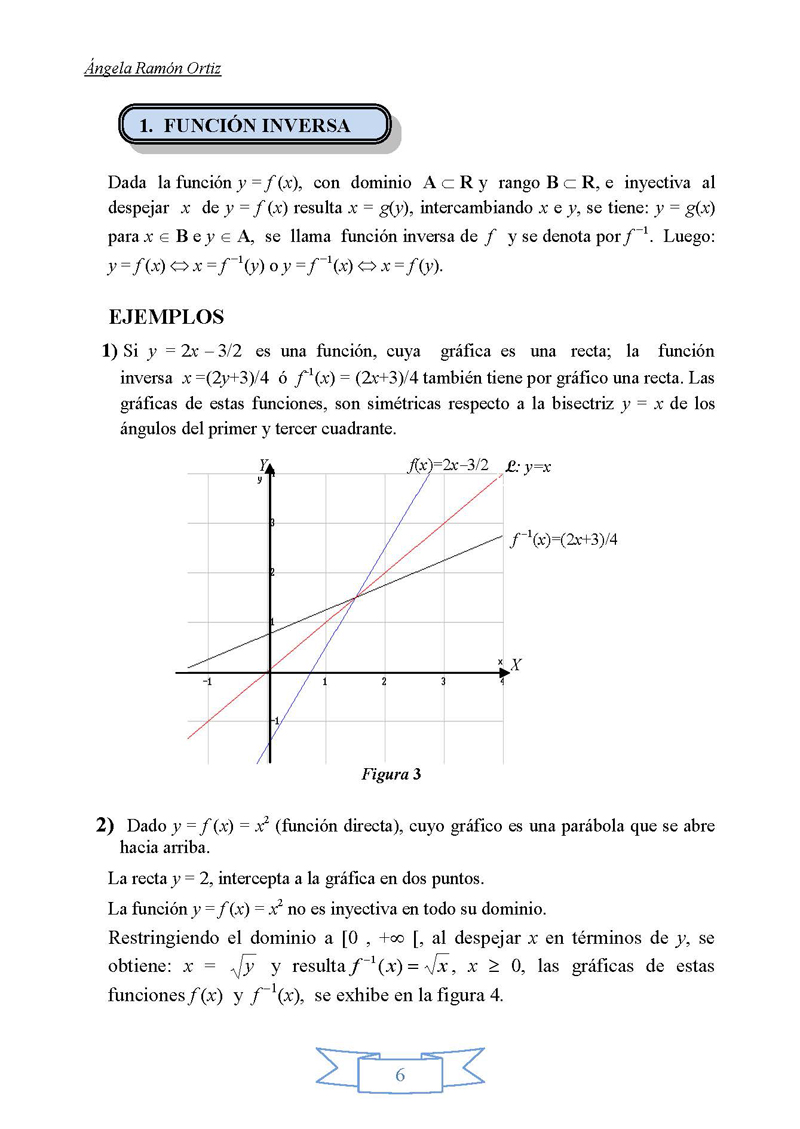
f (x) ? x = f ?1(y) o y = f ?1(x) ? x = f (y). EJEMPLOS 1) Si y =
2x ? 3/2 es una función, cuya gráfica es una recta;
la función inversa x =(2y+3)/4 ó f?1(x) = (2x+3)/4
también tiene por gráfico una recta. Las
gráficas de estas funciones, son simétricas
respecto a la bisectriz y = x de los ángulos del primer y
tercer cuadrante. f(x)=2x?3/2 L: y=x f ?1(x)=(2x+3)/4 X Figura 3
2) Dado y = f (x) = x2 (función directa), cuyo
gráfico es una parábola que se abre hacia arriba.
La recta y = 2, intercepta a la gráfica en dos puntos. La
función y = f (x) = x2 no es inyectiva en todo su dominio.
Restringiendo el dominio a [0 , +? [, al despejar x en
términos de y, se obtiene: x = y y resulta f ?1 ( x) ? x ,
x ? 0, las gráficas de estas funciones f (x) y f ?1(x), se
exhibe en la figura 4. 6

Y Funciones trigonométricas inversas y = x2 L: y= x y= x X
Figura 4 ¡RECUERDE!: Para proceder a estudiar las funciones
trigonométricas inversas es preciso recordar que la
función y = f (x), con dominio A y rango B, sea inyectiva:
1. De y = f (x) se tiene x = g(y), o sea x = f ?1(y) con y = f
(x), y en el dominio de f?1. 2. Intercambiando x e y: y = f ?1(x)
? x = f (y) 3. dominio de f ?1 = rango de f. 4. rango de f ?1 =
dominio f. 5. f ( f ?1(x)) = x, para todo x en el dominio de f
?1. 6. f ?1(f (y)) = y, para toda y en el dominio de f. 7. Las
gráficas de f ?1 y f son simétricas respecto a la
recta y = x. 7

x ? 3 x ? 1 Ángela Ramón Ortiz EJERCICIOS 1)
Analice si la función y ? , admite inversa en su dominio:
a) despeje x en términos de y, en caso fuera posible. b)
grafique la curva correspondiente c) Identifique un intervalo
donde la función es inyectiva 2) Con ayuda de la
circunferencia unitaria, desarrolle según el caso amerite:
a) si sen(?) = 1/3, entonces ? = ………… b) si sen(?) = ?1/2
y cos(?) < 0, entonces ? = ……… c) si tan(?) = ?4/3 y ? ?
]?/2 , ?[, entonces ? = …….. d) si cot(?) = ?1 y sen(?) <
0, entonces ? = ………… Y O (1, 0) X Figura 5 e) si sen(?) =
0, entonces ? = ……………….. f) si cos(?) = 0, entonces ?
= ………………… f) si ? = ?7?/4, entonces cot(?) =
………… 3) De las gráficas estudiadas en la unidad 3,
¿las funciones trigonométricas son
inyectivas?………………. ¿admiten inversa en todo su
dominio? ………………. Al analizar las propiedades y
gráficas de cada una de ellas, nos encontramos con la
dificultad de que ninguna de las funciones trigonométricas
es inyectiva, puesto que son periódicos. Pero podemos
restringir adecuadamente el dominio de las funciones; de tal
manera que estas funciones sean inyectivas, por lo que a las
inversas de estas funciones inyectivas la llamaremos
función inversa de la función trigonométrica
en referencia, así tenemos: 8

Funciones trigonométricas inversas 2. FUNCIÓN
INVERSA DEL SENO Recordando la expresión: y = sen (x).
Dado x ? R, obtendremos el valor de sen(x) = y, como una regla de
correspondencia. R x ? sen ?y R y = sen(x) Figura 6 Dado que el
rango del seno es [?1 , 1], para c ? [?1 , 1], resulta que sen(x)
= c, para algún x ? R, es decir, dado el valor del sen(x)
obtener número real “x”. ¿ …?
?/6 y = sen?1(x) 5?/6 13?/6 1/2 o y = arcsen(x) Figura 7 Por
ejemplo, para x = ?/6, 5?/6, 13?/6, 17?/6, etc. se tiene sen(x) =
1/2, es decir: sen(?/6) = sen(5?/6) = sen(13?/6) = …..= 1/2;
que asegura que la función seno, no es inyectiva. Para
despejar x de y = sen(x) y resulte x = g(y), necesitamos
considerar un dominio adecuado en donde la función seno
sea inyectiva y admita función inversa.
¿Cómo tener el dominio de la función seno a
partir de su gráfica para que sea inyectiva? Para los
intervalos: [?3?/2 , ??/2], [??/2 , ?/2], etc., como dominio la
función resulta inyectiva. Sea el intervalo [??/2 , ?/2]
donde los valores de la función varía desde ….
hasta 1, si x varía desde …… hasta ……. Esta
función restringida (como se muestra en la figura 4-8)
usaremos para definir la función inversa del seno. 9

?1 Ángela Ramón Ortiz Y – 3?/ – ?/2 ?/2 3?/2 2
Figura 8 DEFINICIÓN: La función inversa de la
función seno a la función: sen?1 o Arcsen, cuyo
dominio es el intervalo: [?1 , 1] y el rango [ ??/2 , ?/2],
definida por: Arcsen(x) = sen-1(x) = y ? sen(y) = x. Así,
si y = sen(x), tendremos que x = Arcsen(y). De aquí: y =
Arc sen(x) es la función inversa de la función
seno, donde para todo y ? [??/2 , ?/2] existe un único x ?
[?1 , 1] tal que arcsen(x) = y. OBSERVACIÓN: A la
expresión: Arcsen(x) = y se lee “y es el arco cuyo
seno es x” De la propiedad y = arcsen(x) ? sen(y) = x,
tiene: y ? [??/2 , ?/2], x ? [?1 , 1], se sen(sen?1(y)) =
sen(arcsen(y)) = y, sen (sen(x)) = arcsen(sen(x)) = x, para ?1 ?
y ? 1, para ??/2 ? x ? ?/2 EJEMPLOS: 1) sen(arcsen(1/2)) = 1/2 o
arcsen(1/2) = y ? sen(y) = 1/2, para y ? [??/2 , ?/2]. Se cumple
para y = ?/6. 2) arcsen[sen(??/3)] = ??/3 como ??/3 ? [??/2 ,
?/2], arcsen(??) = y ? ??/3 = sen(y); se cumple para el
único valor y = ? 3 /2, pues sen(??/3) = ? 3 /2 3) Sin
embargo, arcsen(sen(3?/4)) ? 3?/4; pues 3?/4 ? [??/2 , ?/2].
Realizando cálculos sen(3?/4) = sen(? ? ?/4) = sen(?/4), y
luego, arcsen(sen(3?/4)) = ?/4 4) En la gráfica de y =
arcsen(x); ubique los valores de: arcsen(1/2), arcsen(2) y
arcsen(?1/3), en caso de que sea posibles hallarlos. 10

Funciones trigonométricas inversas 5) arcsen(?/3) +
sen(??/6) = 3 /2 ? 1/2 = ( 3 ? 1)/2. 6) Probar que arcsen(1/ 5 )
+ arcsen(2/ 5 ) = ?/2. Para esto, sea ? = arcsen(1/ 5 ) y ? =
arcsen(2/ 5 ), entonces: sen(?) = 1/ 5 y sen(?) = 2/ 5 con E(?) y
E(?) en el I-C. Hay que probar que ? + ? = ?/2, o que sen(?+?) =
sen(?/2), ya que los senos de ángulos iguales son iguales.
Para resolver esto, veremos más adelantes ciertas
propiedades: Y (1, 2) 5 2 (2, 1) 5 1 O 1 2 X Figura 9 EJERCICIOS
1. Encuentre los valores que corresponden a: a) Arcsen(3/5) =
……………….….. d) Arcsen(?12/13) =
………………… b) sen ?1 ( 3 /2 ) =
……….…. c) Arcsen (–1/2) =
……….. e) sen ?1 ( 2 /2) =
………….…. f) Arcsen (–1) =
…………….….. 3. Halle x ?
[??/2 , ?/2], tal que sen(2x) = ?1/2
……………………………….. 4. Halle x ? [?? , 2?],
tal que sen(x/2) = 3 /2 ………………………………….
5. Determine el rango de la función f (x) =
2arcsen[(4?6x)/11]. GRÁFICA DE LA FUNCIÓN y =
arcsen(x): Para graficar la curva y = arcsen(x), tomar los
puntos: (?/2 , 1), (0 , 0), (??/2 , ?1) de la gráfica y =
sen(x), con ??/2 ? x ? ?/2; cuyas coordenadas intercambiadas: (1,
?/2), (0, 0) y (?1,??/2) están en la curva y = arcsen(x).
En la figura 4-10, trace las gráficas de la función
11

1 ? ? ? ? Ángela Ramón Ortiz seno y de arco seno en
los ejes de coordenadas, figuras 10-(a) y 10-(b),
respectivamente. A partir de los puntos descritos y haciendo un
giro alrededor de la recta y = x, se obtiene la gráfica de
y = Arc sen(x): Y L: y= x y = sen(x) Y ?/2 L: y= x y = arcsen(x)
??/2 ?/2 X X ??/2 (a) Figura 10 (b) Complete datos x ??/2 ??/4
??/6 0 ?/6 ?/4 ?/2 .. x ?1 1 ?1/2 0 1 y=sen(x) ?1 ?1/2 0 1/2 y
=sen?1(x) ??/2 ??/4 ??/6 0 ?/6 ?/4 ?/2 Recuerda que el
gráfico de la función y = arcsen(x) que se
construya en la figura 4-10, deben satisfacer las siguientes
propiedades: El dominio es el intervalo [?1 , 1]. El rango de
arcsen es el intervalo [??/2 , ?/2], es decir, ??/2 ? x ? ?/2. La
función y = arcsen(x) se hace nula cuando x = 0. Los
intervalos de signo constante son: Arcsen(x) > 0, para x ? ]0
, 1]; arcsen(x) < 0, para x ? [?1 , 0[. ? La función y
= srcsen(x) es creciente sobre el intervalo [?1 , 1], obteniendo
su valor mínimo, igual a ??/2 en el extremo izquierdo del
intervalo; y, el valor máximo igual a ?/2 en el extremo
derecho del intervalo [?1 , 1]. 12

Funciones trigonométricas inversas ? La gráfica de
la función y = arcsen(x) es simétrico respecto al
origen de coordenadas, así los puntos (?/2 , 1) y (?1 ,
??/2), pertenecen a la gráfica. RECUERDE: se escoge el
valor de y en el rango [??/2 , ?/2] del arcsen. Función .y
= arcsen(1/2) .y = arcsen(?1/2) .y = arcsen(?1) Expresión
equivalente sen(y) = 1/2 y ??/2 ? y ? ?/2 ……………….. y
………………. ……………….. y ……………….
solución y = ?/6 ……………………………..
……………………………. .y = arcsen(? .y = arcsen(? .y
= arcsen(0) 2 /2) 3 /2) ……………….. y
………………. ……………….. y ……………….
……………….. y ……………….
…………… y
…………….
…………………………….
……………………………….
………………………………
……………………
3. FUNCIÓN INVERSA DEL COSENO ¿Cómo
restringir el dominio de la función coseno de modo que
resulte inyectiva? Al trazar una horizontal en y = 1/2, en la
curva y = cos(x), se observa que cos(?2?) =cos(0) = cos(2?) = 1,
por tanto la función coseno no es inyectiva. Se observa
que la función es inyectiva en los intervalos: [?2? , ??],
[?? , 0], [0 , ?], [? , 2?], etc. De estos consideremos el
intervalo [0 , ?] donde los valores de la función
varía desde …… hasta ?1, si x varía desde ….
hasta ….. Esta función restringida sirve para definir la
función inversa del coseno. Y -2? -? 0 ? 2? X Figura
Figura 11 11 DEFINICIÓN: La función inversa de la
función coseno es la función: cos?1 o arccos, cuyo
dominio es el intervalo: [?1 , 1] y el rango [0 , ?], donde:
Arccos(x) = cos?1(x) = y ? cos(y) = x. 13

Ángela Ramón Ortiz Así, si y = cos(x) se
tiene x = Arccos(y). De donde: y = Arccos(x) es la función
inversa de y = cos(x). De esta manera para y ? [0 , ?] existe un
único x ? [?1 , 1] tal que arccos(x) = y.
OBSERVACIÓN: arccos(x) = y se lee “y es el arco cuyo
coseno es x” De la propiedad y = arccos(x) ? cos(y) = x, y
? [0 , ?], x ? [?1 , 1], se tiene: cos(cos?1(y)) = cos(arccos(y))
= y, cos?1(cos (x)) = arccos(cos(x)) = x, para ?1 ? y ? 1, para 0
? x ? ?, EJEMPLOS: 1) cos[arccos(3/5)] = 3/5, puesto que 3/5 ?
[?1 , 1]. 2) Arccos[cos(?/4)] = arccos( 2 /2), puesto que ?/4 ?
[0 , ?] y 2 /2 ? [?1 , 1]. 3) Arccos[cos(??/3)] ? ??/3. Pues:
cos(??/3) = cos(? ? 2?/3) = cos(?/3), del cual, arccos(cos(??/3))
= ?/3 4) En la gráfica de y = arccos(x), determine:
arccos(1/2), arccos(2) y arccos(?1/3), en caso de que sean
posibles. 5) Para evaluar cos[arcsen(3/5)]. Sea ? = arcsen(3/5),
entonces sen(?) = 3/5, como ? está en el I-cuadrante, se
tiene que cos(?) = 4/5. RECUERDE: que es esencial escoger el
valor de y en el rango [0 , ?] de arccos. Función
Expresión equivalente solución .y = arccos(1/2)
cos(y) = 1/2 y 0 ? y ?? . y = ?/3 .y = arccos(?1/2) .y =
arccos(1) ……………….. y ……………….
……………….. y ……………….
……………………………..
……………………………. .y = arccos(? .y = arccos(? .y
= arccos(0) 2 /2) 3 /2) ……………….. y
………………. ……………….. y ……………….
……………….. y ……………….
…………………………….
……………………………….
…………………………… GRÁFICA DE LA
FUNCIÓN y = arccos(x): Para dibujar la curva y =
arccos(x), tomaremos las coordenadas de cada punto de la curva y
= cos(x), sobre 0 ? x ? ? , intercambiando de posición las
coordenadas: (0 , 1), (?/2 , 0), (? , ?1) pertenecen a la
gráfica de y = cos(x), se tiene que (1 , 0), (0 , ?/2),
(?1 , ?) 14

x x 0 Funciones trigonométricas inversas pertenecen a la
gráfica de y = arccos(x). Estando la gráfica de y =
cos(x) en los intervalos establecidos, se tiene la gráfica
de y = Arccos(x), haciendo un giro alrededor de la recta y = x.
(figura 12). Y O L: y= x .y = x y =cos(x) DECRECIENTE X (? , ?1)
(?1,?) y = cos?1(x) y = arccos(x) DECRECIENTE O Y ? (?/2 , 0) .y
= x X (a) Gráfica de la función coseno, restringida
Figura 12 (b) Gráfica de la función inversa del
seno. Complete datos 0 ?/6 ?/4 ?/3 ?/2 3?/4 5?/6 … ?1 …
… 0 … … y=cos(x) 1 y= arccos(x) 0 ?/2 Desde
el gráfico, podemos anotar las siguientes propiedades de
la función y = arccos(x): ? El dominio es el intervalo [..
, ..]. ? El conjunto de valores o rango es el intervalo [… ,
?]. ? La función arccos(x) toma valor cero: arccos(x) = 0,
para x = ……. ? El valor de la función : arcscos(x) ?
……, para todo x ?[?1 , 1]. ? La función arccos(x) es
decreciente en el intervalo [?1 , 1], siendo su valor
máximo igual a ?, en el extremo …………… del
intervalo; y, el valor mínimo igual a ……, en el
extremo derecho del intervalo [?1 , 1]. ? La curva y = arccos(x)
no es simétrica respecto al origen de coordenadas ni a los
ejes coordenados. EJERCICIOS 1. Encuentre los valores que
corresponden a: a)arccos(?4/5) = ………….. d)
sen[arcsen(1/2)] +cos[ arccos(1/3)] = ……. 15

2 -1 Ángela Ramón Ortiz b) arccos(?5/13) =
……….. e) arcsen[sen(30º)] + arcos[cos(10º)] =
………. c) arccos(?1/2) = ………….. f)
arcsen[sen(60º)] + arcos[cos(53º)] = ……. 2.
¿Existe respuesta para Cos ?1 (2,5)? ……… ¿Por
qué? ……………………………. 3. Evalúe
el valor de sen[arccos(?2/3)] 4. Calcule: 5 tan[ 1 arcsen (41/
41)] 4.4. FUNCIÓN INVERSA DE LA TANGENTE
¿Cuál es un intervalo sobre el cual la
función y = tan(x) es inyectiva? Observe la gráfica
y = tan(x) (figura 4-13), la función está definida
por tramos: ]?3?/2 , ??/2[ , ]??/2 , ?/2[, ]?/2 , 3?/2[, etc. y
tomamos el intervalo ]??/2 , ?/2[ para definir la función
inversa de la tangente. -3?/2 -?/2 ?/2 3?/2 Figura 13 La
función inversa de la tangente, denotado por tan?1 o
arctan se llama arco tangente y se define mediante: arctan : R ??
] ??/2 , ?/2[ , donde arctan(x) = y ? tan(y) = x Así, si y
= tan(x) se tiene x = arctan(y). De esto y = Arctan(x) es la
función inversa de y = tan(x). De y = arctan(x) ? x =
tan(y), resulta: tan(tan-1(x)) = tan(arctan(x)) = x, tan (tan
(y)) = arctan(tan(y)) = y, (x es un número real
cualquiera), para ??/2 < y < ?/2, 16

Funciones trigonométricas inversas EJEMPLOS: 1)
tan(arctan(1)) = tan(?/4) = 1 2) arctan(tan(?/3)) = arctan( 3 ) =
?/3 3) arctan?tan(?3? / 4)? ? ?3? / 4 , puesto que el
ángulo ?3?/4 sale de los límites del intervalo
]??/2 , ?/2[. Pero arctan[tan(?3?/4)] = arctan(tan(? ?3?/4)) =
arctan(1) = ?/4, de donde arctan(tan(?3?/4) = ?/4. 4) En la
gráfica de la función y = arctan(x), determine:
arctan(2), arctan(7) y arctan(?3), en caso de que sean posibles.
GRÁFICA DE LA FUNCIÓN y = arctan(x): La curva y =
arctan(x), coincide con la curva de la función x =
arctan(y), cuando la variable y varía en el intervalo
]??/2 , ?/2[, como se muestra a continuación (figura 14).
IMPORTANTE Trace la gráfica de y = tan(x) L: y= x y =
arctan(x) arco tangente reflejando la curva tangente dada
respecto a la recta y=x, guíate en los puntos (??/4 , ?1),
(0 , 0) y (?/4 , 1), pertenecen a la tangente, y sus
correspondientes simétricos respecto a y = x, son (?1 ,
??/4), (0 , 0) y (1 , ?/4). Asimismo, la asíntotas
verticales x =??/2, x = ?/2 se convierten en asíntotas
horizontales Gráfica de la función tangente,
restringida Figura 14 En el gráfico anterior (figura 14),
notamos algunas propiedades de la función y = arctan(x):
17

? ? ? ? Ángela Ramón Ortiz El dominio es el
conjunto …… de los números reales. El conjunto de
valores o rango es el intervalo ]… , …[. Los ceros de la
función son: arctan(x) = 0, para x = ….. Los intervalos
de signo constante son: arctan(x) > 0, para x ? ]… , … [;
arctan(x) < …, para x ? [??, 0[. ? La función
arctan(x) es …………, sobre todo su dominio. ? La
gráfica de arctan(x) es simétrico respecto al
…………………………….. 5. FUNCIONES INVERSAS DE LA
COT, SEC Y CSC De manera análoga a como hemos razonado
para las funciones inversas del seno, coseno y tangente, se
procede para las funciones trigonométricas cotangente,
secante, cosecante cuyas gráficas se construyen a partir
de las funciones restringidas (figura 15): Y L: y= x Y L: y= x y
= cot (x) restringida a [0 , ?] Y X y = sec (x) restringida a [0
, ?] L: y= x Trace las gráficas de las inversas de las
funciones restringidas que se X X exhiben. y = csc (x)
restringida a [??/2 , ?/2] Figura 15 18

2 Funciones trigonométricas inversas EJERCICIOS: Halle el
valor de x, en cada caso: a) sen(x) = ?1/2 b) cos(x) = 3 /2 c)
arcsen(x) = ?/2 d) arctan(x) = 2. e)sen(2x) = 2 /2, x ? [0 , 2?]
f) cos(x/2) = ?1. Comprueba tu aprendizaje 1.
¿Cuáles de las siguientes funciones reales de
variable real admiten inversa? a) f (x) = x2 + 2 c) h(x) = 2x ? 5
2. Calcule: a) E = arctan(1) + arctan( 3 ) c) E = arccos( 3 /2) +
arcsen(?1/2) 3. Calcule: a) cos(arcsen(0,8)) c) cos[2arctan( 3 )
– arcsen(1/2)] 4. Calcule: a) sen[arccos(?1/2) +
arc(tan(4/3))] c) cos[arctan( 3 /2) – arcsen(12/13)] b)
g(x) = 2×3 d) i(x) = 1/x + 1 b) E = arcsec(2) + arcsec( 2 ) d) E
= arcsen(5/7) + arccos(5/7) b) tan[ 1 arccos(1/2)] d)
sen(2arcsen(x)), (0 < x < 1) b) tan[arcsen(?1/3) –
arccos(2/3)] d)cot[arctan(?2/3)]+ arccos[tan(?12/5)] 5. Analice
el cumplimiento de las siguientes propiedades: a) arctan(1) +
arctan(1/2) = arctan(3) c) sen[arccos(?1/2)] = ?1/2 6. Demuestre
las siguientes identidades: a) 2arctan(1/2) = arctan(4/3) c)
arcsen(4/5) + arcsen(3/4) = ?/2 b) 2arccos(x) = ?. c)
cos[arcsen(4/5) + arctan(3/4)] = 1 b) 2arctan(1/3) + arctan(1/7)
= ?/4 d) arccos(12/13) + arctan(1/4) = arccot(43/32) 7. a) Pruebe
que: si –1 < x < 1, entonces arcsen(x) + arccos(x) =
?/2. b) si sen(?) = y con 0 < y <1. Exprese en
términos del arcsen el arccos y el arctan 19
Ángela Ramón Ortiz c) Determine la verdad o
falsedad de: arcsen(3/5) = arccos(4/5) = arctan(3/4). d) Halle el
intervalo de variación de “?” para
arcsen[(?+1)/2]. 8. Completa en los espacios subrayados: a) La
función inversa de la tangente se denota
…………………………………………. b) La
función tangente inversa se define como la inversa de la
función ……….. restringida al Dominio ]??/2 , ?/2[.
c) El dominio de la función Tangente inversa es
………………………………………… d) El rango de
la función Tangente inversa es
……………………………………………. 9. Trace el
gráfico de las siguientes funciones: a) y = arcsen(x) + 1
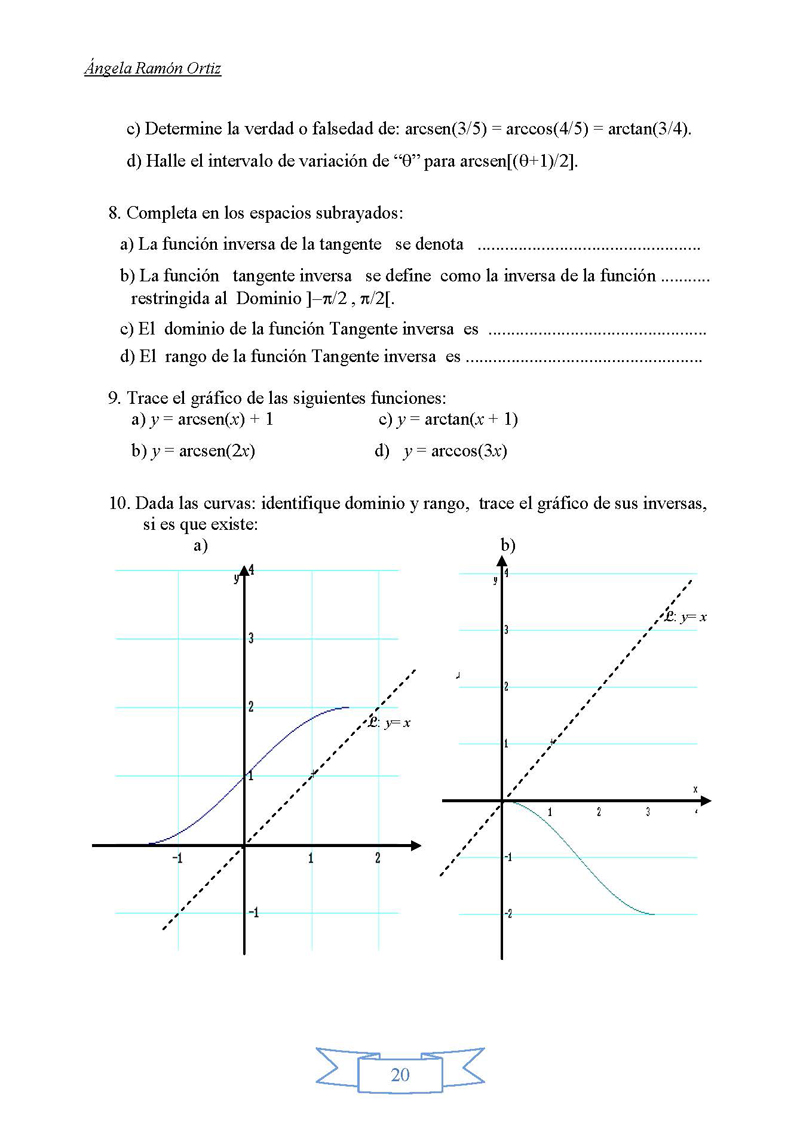
b) y = arcsen(2x) c) y = arctan(x + 1) d) y = arccos(3x) 10. Dada
las curvas: identifique dominio y rango, trace el gráfico
de sus inversas, si es que existe: a) L: y= x 20 L: y= x b) L: y=
x

Funciones trigonométricas inversas BIBLIOGRAFÍA 1.
BOYLE, Patrick (1990) Trigonometría con Aplicaciones: Con
ejercicios para calculadora. México D.F. : Harla. 2.
HAASER, N., LASALLE, J. & SUVILLAN, J. (1980) Análisis
Matemático I. Curso de introducción. México
D.F.: Editorial Trillas 3. NICHOLS, E. & GARLAND, E. (1975)
Trigonometría Moderna. México: Editorial
Continental S.A. 4. SWOKOWSKI, E. (1996) Álgebra y
Trigonometría con Geometría Analítica.
México D.F.: Editorial Iberomaricana, S.A. de C.V. 5.
TSIPKIN, A. (1985) Manual de matemáticas para la
enseñanza media. Moscú: Editorial Mir. 6.
SAÉNZ, Jorge (S/A) Vectores, geometría y
trigonometría. Lima: Pontificia Universidad
Católica del Perú. 7. SCHOOL MATHEMATICS STUDY GOUP
(1965) Matemática para la Escuela Secundaria. Funciones
Elementales. Washington: organización de los Estados
Americanos. 21
