
Todos sabemos que el estudio de “Matemática”
implica conocer y familiarizarse con enunciados, reglas,
propiedades, conceptos, teoremas, procedimientos y muchas cosas
mas. Pero resulta interesante destacar que toda la estructura de
esta ciencia, desde la mas elemental
“aritmética”, hasta los mas complejos
desarrollos del “análisis matemático”
se basan en dos conceptos (que se consideran fundamentales): El
primero es la noción de “NÚMERO”; el
segundo es el concepto de “FUNCIÓN”. Se
podría decir que éstos son como las dos
“piernas” o “columnas” sobre las que se
asientan la totalidad de los capítulos en que puede
dividirse la compleja estructura que forma la
“Matemática actual”. Este trabajo se refiere,
con cierto detalle, al concepto de “FUNCIÓN” y
a las diferentes e infinitas formas que pueden adoptar en general
“las FUNCIONES”. Funciones matemáticas

3 Funciones; conceptos básicos: En el mundo que nos rodea
existen muchos ejemplos sencillos de la noción de
función . En efecto supongamos un simple viaje en taxi.
Claramente en este caso hay dos variables que son, una la
“distancia a recorrer (d)” y la otra el “precio
del viaje (p)”. Por supuesto que todos sabemos que a cada
distancia “d” le corresponde un precio
”p” y solo uno. En este ejemplo las dos variables
tienen una diferencia fundamental; mientras que la distancia
“d” la impone el pasajero de acuerdo a su necesidad,
el precio del viaje “p” lo suministra el sistema. La
variable “d es independiente” pero la variable
“p es dependiente” de la primera. Si aceptamos que la
palabra “depende”, puede reemplazarse por la
expresión “es función”, podemos decir
que el precio del viaje “depende” o “es
función “de la distancia recorrida. No hay
ningún inconveniente en usar el siguiente simbolismo: p =
f (d) y decir que “p” es función de
“d”. Funciones matemáticas

4 Se puede generalizar lo anterior y definir
“función” empleando un lenguaje sencillo, pero
no demasiado riguroso. Se dice que una variable “y”
es función de otra variable “x”, cuando entre
ellas existe una expresión matemática tal que, a
cada valor de “x” le hace corresponder un valor de
“y” y sólo uno. y = f(x) Esta correspondencia
“uno a uno” entre las variables se conoce como
“unívoca”. La variable “x” se
llama “variable independiente” o
“argumento”, mientras que a la “y” se la
conoce como “variable dependiente” o
“función”. El conjunto de valores que pueden
ser asignados a “x” se llama “Dominio D”
o “conjunto de partida” mientras que se conoce como
“Codominio CD” o “conjunto de llegada”,
el que agrupa a los valores que puede tomar “y”.
Dentro del codominio pueden existir elementos que no se
correspondan con elementos del dominio; en ese caso se puede
definir como “conjunto imagen” al que contiene solo
aquellos valores que coincidan, por la función, con
elementos del conjunto “x”. Funciones
matemáticas

5 Destacamos que una función no es la expresión
matemática o fórmula que relaciona a las variables,
sino que es el conjunto de todos los pares ordenados ( ???? ;
???? ) que satisfacen a la expresión dada. No obstante,
suele decirse que la fórmula define a la función,
pero resulta indispensable expresar claramente el
“dominio” de la misma. Varios son los métodos
de representación de las funciones: 1° – Mediante
diagramas de Venn 2° – Con una matriz de dos columnas en
correspondencia con las variables x e y . 3° – Mediante un
gráfico Cartesiano. Nos apoyaremos en un cuadro de valores
o matriz, para lo cual, utilizando la expresión dada, se
calcularán en cada caso los valores numéricos
correspondientes a “y”, para cada valor
numérico arbitrario de “x”. Si bien el
número de puntos que se calculen es obviamente limitado,
una razonable interpolación gráfica
permitirá conocer la “forma” de la
función llevando los pares a coincidir con los puntos de
un “grafico Cartesiano”. Debemos considerar que las
expresiones matemáticas que relacionan a las variables son
“infinitas”. Se tratará de probar esta
afirmación, pero para un estudio sistemático de las
funciones las agruparemos en “familias” con
características particulares. Funciones
matemáticas

1. 6 Primera clasificación de las funciones
matemáticas: Funciones Algebraicas Funciones
Matemáticas Funciones Trascendentes Funciones Especiales
Pero veremos una clasificación mas detallada: Funciones
matemáticas

2. 7 Racional Entera Lineal o de 1° grado Cuadrática o
de 2° grado Cúbica o de 3° grado Polinomio general
grado “n” Funciones Algebraicas Racional Fraccionaria
Hiperbólica Homográfica Fraccionaria General
Irracional Funciones matemáticas

8 3. Funciones Trascendentes Exponencial Logarítmica
Trigonométricas Hiperbólicas Creciente Decreciente
Log. Decimales Log. Naturales Directas: Sen, Cos, Tg, Ctg, Sec y
Cosec Inversas: arc.sen, arc.cos, etc. Directas Sh, Ch, Th.
Inversas: arg.sh, arg.ch, etc. Funciones matemáticas

4. 9 Lineales Módulo Signo Parte Entera Mantisa Funciones
Especiales Operaciones entre funciones. Suma, Resta, Producto y
Cociente Compuesta o función de función.
Paramétricas Definida por tramos Funciones
matemáticas

5. 10 Algebraicas Racional Entera Racional Fraccionaria
Irracional Exponencial Lineal o de 1° grado Cuadrática
o de 2° grado Cúbica o de 3° grado Polinomio
general grado “n” Hiperbólica
Homográfica Fraccionaria General Creciente Decreciente
Funciones Matemáticas Trascendentes Logarítmica
Trigonométricas Log. Decimales Log. Naturales Directas:
Sen, Cos, Tg, Ctg, Sec y Cosec Inversas: arc.sen, arc.cos, etc.
Hiperbólicas Lineales Operaciones entre Directas Sh, Ch,
Th. Inversas: arg.sh, arg.ch, etc. Módulo Signo Parte
Entera Especiales funciones. Compuesta o función de
función. Paramétricas Definida por tramos Funciones
matemáticas Mantisa

11 Coordenadas Cartesianas Ortogonales y +y Eje de ordenadas
P(x;y) 1° cuadrante 2° cuadrante a = ángulo de una
recta -x 3° cuadrante x -y Funciones matemáticas
Origen (0;0) 4° cuadrante +x Eje de abcisas

12 Funciones desde el comienzo 1. F. Lineal 2. F.
Cuadrática 3. F. Cúbica 4. F. Polinomio gral. 5. F.
Hiperbólica 6. F. Homográfica 7. F. Racional
fraccionaria 8. F. Irracional 9. F Exponencial 10. F
Logarítmica Elem. de Trigonometría 11. F.
Trigonométricas 12. F. Trigonomét. Inversas 13. F.
Hiperbólicas Trascen. 14. F. Hiperb. Inversas 15. F.
Especiales lineales 16. Operaciones entre Func. 17. F. Compuesta
o F de F. 18. F. Paramétricas 19. F. definidas por tramos
Apéndice Funciones matemáticas

13 1 – Función de 1° grado o Función Lineal
y=ax + b Funciones matemáticas

14 La primera función que se estudia es la llamada:
Función lineal: y=ax + b El nombre de “lineal”
es debido a que, como se verá, en todos los casos la
representación cartesiana de esta función es una
“línea recta” situada en algún lugar
del plano. El dominio y el codominio, debido a su simpleza, se
extiende a todos los números reales: R Como ejemplo
tomemos la expresión: y=2x+3 Dándole a la variable
“x” valores numéricos cualesquiera, se
calculan los correspondientes valores de “y”. Luego
se puede construir el siguiente “cuadro” o
“tabla de valores”: X 1 2 3 -2 -3,5 0 Y 5 7 9 -1 4 3
Cada par de valores (x;y) se puede representar en un
gráfico cartesiano por un punto, haciéndole
corresponder al mismo las coordenadas (x;y) en ese orden. Si se
unen con un trazo continuo los puntos indicados, se verá
que están alineados según una recta. Se pueden
obtener por cálculo todos los pares (x;y) de valores que
se deseen y los puntos que se grafiquen seguirán estando
sobre la recta anterior. Los infinitos pares de valores (x;y)
tienen una correspondencia biunívoca con los infinitos
puntos de la recta. Por supuesto que, se puede trazar la recta
correspondiente, calculando solo dos puntos cualesquiera (dos
puntos determinan una recta). Funciones matemáticas
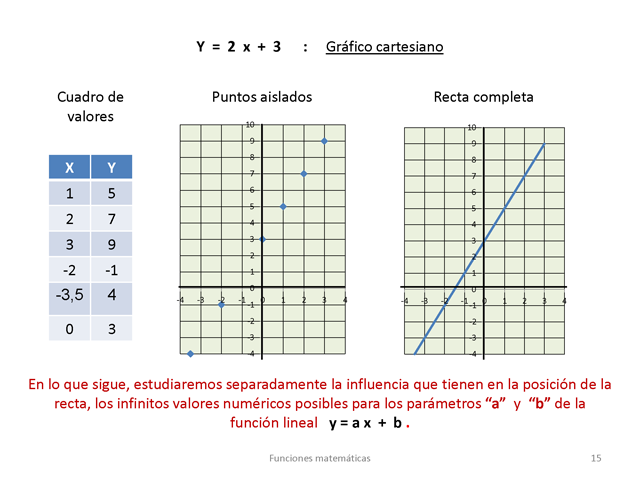
: 15 Y = 2 x + 3 Gráfico cartesiano Cuadro de valores
Puntos aislados 10 9 Recta completa 10 9 X 1 2 3 -2 Y 5 7 9 -1 8
7 6 5 4 3 2 1 8 7 6 5 4 3 2 1 -3,5 4 -4 -3 -2 -1 0 -1 0 1 2 3 4
-4 -3 -2 -1 0 -1 0 1 2 3 4 0 3 -2 -3 -4 -2 -3 -4 En lo que sigue,
estudiaremos separadamente la influencia que tienen en la
posición de la recta, los infinitos valores
numéricos posibles para los parámetros
“a” y “b” de la función lineal y =
a x + b . Funciones matemáticas

8 6 4 2 16 Función lineal: y = a x + b ; para: 0 < a
< 8 (siempre positivo) y b = 0 10 Comenzamos con: y = 1 x
(celeste) Y luego al coeficiente “a”, le asignamos
varios valores menores que 1. 0 -10 -8 -6 -4 -2 0 2 4 6 8 10 -2
-4 -6 -8 -10 Funciones matemáticas

8 6 4 2 17 Función lineal: y = a x + b ; para: 0 < a
< 8 (siempre positivo) y b = 0 10 Comenzamos con: y = 1 x
(celeste) Y luego al coeficiente “a”, le asignamos
varios valores menores que 1. y = 0,1 x (azul) -10 -8 -6 -4 -2 0
0 2 4 6 8 10 -2 -4 -6 -8 -10 Funciones matemáticas

8 6 4 2 18 Función lineal: y = a x + b ; para: 0 < a
< 8 (siempre positivo) y b = 0 10 Comenzamos con: y = 1 x
(celeste) Y luego al coeficiente “a”, le asignamos
varios valores menores que 1. y = 0,1 x (azul) -10 -8 -6 -4 -2 0
0 2 4 6 8 10 y = 0,3 x (rojo) Funciones matemáticas -2 -4
-6 -8 -10

8 6 4 2 19 Función lineal: y = a x + b ; para: 0 < a
< 8 (siempre positivo) y b = 0 10 Comenzamos con: y = 1 x
(celeste) Y luego al coeficiente “a”, le asignamos
varios valores menores que 1. y = 0,1 x (azul) -10 -8 -6 -4 -2 0
0 2 4 6 8 10 y = 0,3 x y = 0,5 x (rojo) (verde) Funciones
matemáticas -2 -4 -6 -8 -10

8 6 4 2 20 Función lineal: y = a x + b ; para: 0 < a
< 8 (siempre positivo) y b = 0 10 Comenzamos con: y = 1 x
(celeste) Y luego al coeficiente “a”, le asignamos
varios valores menores que 1. y = 0,1 x (azul) -10 -8 -6 -4 -2 0
0 2 4 6 8 10 y = 0,3 x y = 0,5 x Y = 0,8 x (rojo) (verde)
(violeta) Funciones matemáticas -2 -4 -6 -8 -10

8 6 4 2 -2 -4 -6 -8 21 Función lineal: y = a x + b ; para:
0 < a < 8 (siempre positivo) y b = 0 10 Comenzamos con: y =
1 x (celeste) Y luego al coeficiente “a”, le
asignamos varios valores menores que 1. y = 0,1 x (azul) -10 -8
-6 -4 -2 0 0 2 4 6 8 10 y = 0,3 x y = 0,5 x Y = 0,8 x (rojo)
(verde) (violeta) Funciones matemáticas -10 Si
”a” es menor que 1, el ángulo a aumenta desde
0°, pero no sobrepasa los 45°
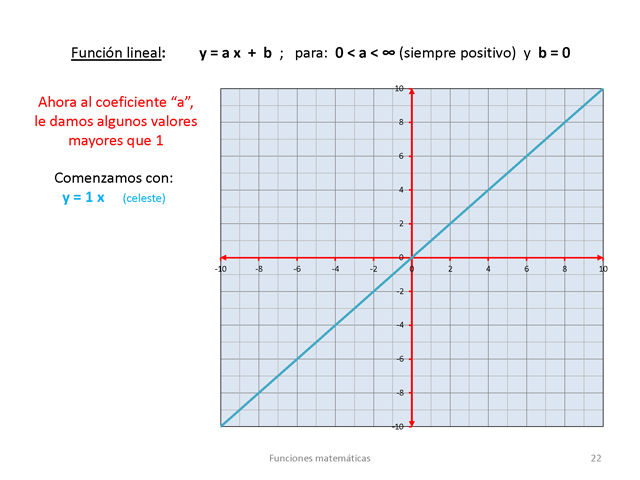
8 4 22 Función lineal: y = a x + b ; para: 0 < a < 8
(siempre positivo) y b = 0 10 Ahora al coeficiente
“a”, le damos algunos valores mayores que 1 6
Comenzamos con: y = 1 x (celeste) 2 0 -10 -8 -6 -4 -2 0 2 4 6 8
10 -2 -4 -6 -8 -10 Funciones matemáticas

8 4 23 Función lineal: y = a x + b ; para: 0 < a < 8
(siempre positivo) y b = 0 10 Ahora al coeficiente
“a”, le damos algunos valores mayores que 1 6
Comenzamos con: y = 1 x (celeste) 2 y = 1,5 x (naranja) 0 -10 -8
-6 -4 -2 0 2 4 6 8 10 -2 -4 -6 -8 -10 Funciones
matemáticas

8 4 24 Función lineal: y = a x + b ; para: 0 < a < 8
(siempre positivo) y b = 0 10 Ahora al coeficiente
“a”, le damos algunos valores mayores que 1 6
Comenzamos con: y = 1 x (celeste) 2 y = 1,5 x (naranja) 0 -10 -8
-6 -4 -2 0 2 4 6 8 10 y= 3x ( azul) -2 -4 -6 -8 -10 Funciones
matemáticas

8 4 25 Función lineal: y = a x + b ; para: 0 < a < 8
(siempre positivo) y b = 0 10 Ahora al coeficiente
“a”, le damos algunos valores mayores que 1 6
Comenzamos con: y = 1 x (celeste) 2 y = 1,5 x (naranja) 0 -10 -8
-6 -4 -2 0 2 4 6 8 10 y= 3x ( azul) -2 y = 10 x (rojo) Funciones
matemáticas -4 -6 -8 -10

8 4 -6 26 Función lineal: y = a x + b ; para: 0 < a
< 8 (siempre positivo) y b = 0 10 Ahora al coeficiente
“a”, le damos algunos valores mayores que 1 6
Comenzamos con: y = 1 x (celeste) 2 y = 1,5 x (naranja) 0 -10 -8
-6 -4 -2 0 2 4 6 8 10 y= 3x ( azul) -2 y = 10 x y = 100 x (rojo)
(verde) Funciones matemáticas -4 -8 -10

8 6 4 2 -6 27 Función lineal: y = a x + b ; para: 0 < a
< 8 (siempre positivo) y b = 0 10 Ahora al coeficiente
“a”, le damos algunos valores mayores que 1
Comenzamos con: y = 1 x (celeste) Cuando el valor de
“a” es > 1, el ángulo aumenta desde
45°, pero no sobrepasa los 90°. y = 1,5 x (naranja) 0 -10
-8 -6 -4 -2 0 2 4 6 8 10 y= 3x ( azul) -2 y = 10 x y = 100 x
(rojo) (verde) Funciones matemáticas -4 -8 -10

6 4 2 0 -2 28 Función lineal: y = a x + b ; para: 0 < a
< 8 (siempre positivo) y b = 0 y = 0,1 x y = 0,3 x y = 0,5 x Y
= 0,8 x y=1x (azul) (rojo) (verde) (violeta) (celeste) Y ahora
tenemos todo el haz de rectas con “a” positivo. 10 8
-10 -8 -6 -4 -2 0 2 4 6 8 10 y = 1,5 x (naranja) y= 3x ( azul) -4
y = 10 x y = 100 x (rojo) (verde) Funciones matemáticas -6
-8 -10

4 2 0 -2 -6 -8 29 Función lineal: y = a x + b ; para: 0
< a < 8 (siempre positivo) y b = 0 10 y = 0,1 x y = 0,3 x y
= 0,5 x Y = 0,8 x y=1x (azul) (rojo) (verde) (violeta) (celeste)
8 6 -10 -8 -6 -4 -2 0 2 4 6 8 10 y = 1,5 x (naranja)
Conclusión: Si el y= 3x ( azul) -4 coeficiente
“a” es positivo, la orientación y = 10 x y =
100 x (rojo) (verde) Funciones matemáticas -10 de la recta
es del 1° al 3° cuadrante, en todos los casos. El
ángulo varía desde 0° hasta 90°.°

8 6 30 Función lineal: y = a x + b ; para: 0 > a > –
8 (siempre negativo) y b = 0 10 A continuación al
coeficiente “a”, le damos valores entre – 8 y
-1 (valores negativos). 4 y = – 100 x (verde) 2 0 -10 -8 -6 -4 -2
0 2 4 6 8 10 -2 -4 -6 -8 -10 Funciones matemáticas

8 6 31 Función lineal: y = a x + b ; para: 0 > a > –
8 (siempre negativo) y b = 0 10 A continuación al
coeficiente “a”, le damos valores entre – 8 y
-1 (valores negativos). 4 y = – 100 x y = – 10 x (verde) (rojo) 2
0 -10 -8 -6 -4 -2 0 2 4 6 8 10 -2 -4 -6 -8 -10 Funciones
matemáticas

8 6 32 Función lineal: y = a x + b ; para: 0 > a > –
8 (siempre negativo) y b = 0 10 A continuación al
coeficiente “a”, le damos valores entre – 8 y
-1 (valores negativos). 4 y = – 100 x y = – 10 x (verde) (rojo) 2
0 y= -3x ( azul) -10 -8 -6 -4 -2 0 2 4 6 8 10 -2 -4 -6 -8 -10
Funciones matemáticas

8 6 -4 33 Función lineal: y = a x + b ; para: 0 > a
> – 8 (siempre negativo) y b = 0 10 A continuación al
coeficiente “a”, le damos valores entre – 8 y
-1 (valores negativos). 4 y = – 100 x y = – 10 x (verde) (rojo) 2
0 y= -3x ( azul) -10 -8 -6 -4 -2 0 2 4 6 8 10 -2 y = – 1,5 x
(naranja) Funciones matemáticas -6 -8 -10

8 6 4 2 -4 -6 34 Función lineal: y = a x + b ; para: 0
> a > – 8 (siempre negativo) y b = 0 10 A
continuación al coeficiente “a”, le damos
valores entre – 8 y -1 (valores negativos). Cuando
“a” se hace negativo, la recta sobrepasa los 90°.
El ángulo “a” va hasta y = – 100 x y = – 10 x
(verde) (rojo) 0 135°, conforme el valor crece hasta -1. y=
-3x ( azul) -10 -8 -6 -4 -2 0 2 4 6 8 10 -2 y = – 1,5 x y=-1x
(naranja) (celeste) Funciones matemáticas -8 -10

8 6 2 35 Función lineal: y = a x + b ; para: 0 > a >
– 8 (siempre negativo) y b = 0 10 Y finalmente el coeficiente
“a” variará entre -1 y 0 (valores negativos).
4 y=-1x (celeste) 0 -10 -8 -6 -4 -2 0 2 4 6 8 10 -2 -4 -6 -8 -10
Funciones matemáticas

8 6 2 0 36 Función lineal: y = a x + b ; para: 0 > a
> – 8 (siempre negativo) y b = 0 10 Y finalmente el
coeficiente “a” variará entre -1 y 0 (valores
negativos). 4 y=-1x Y = – 0,8 x (celeste) (violeta) -10 -8 -6 -4
-2 0 2 4 6 8 10 -2 -4 -6 -8 -10 Funciones
matemáticas

8 6 2 0 -2 37 Función lineal: y = a x + b ; para: 0 > a
> – 8 (siempre negativo) y b = 0 10 Y finalmente el
coeficiente “a” variará entre -1 y 0 (valores
negativos). 4 y=-1x Y = – 0,8 x (celeste) (violeta) -10 -8 -6 -4
-2 0 2 4 6 8 10 y = – 0,5 x (verde) Funciones matemáticas
-4 -6 -8 -10

8 6 2 0 -2 -4 38 Función lineal: y = a x + b ; para: 0
> a > – 8 (siempre negativo) y b = 0 10 Y finalmente el
coeficiente “a” variará entre -1 y 0 (valores
negativos). 4 y=-1x Y = – 0,8 x (celeste) (violeta) -10 -8 -6 -4
-2 0 2 4 6 8 10 y = – 0,5 x (verde) y = – 0,3 x (rojo) -6 -8 -10
Funciones matemáticas

8 6 4 2 0 -2 -4 39 Función lineal: y = a x + b ; para: 0
> a > – 8 (siempre negativo) y b = 0 10 Y finalmente el
coeficiente “a” variará entre -1 y 0 (valores
negativos). El ángulo “a” sigue creciendo
hasta el valor 180°, para a=0 y=-1x Y = – 0,8 x (celeste)
(violeta) -10 -8 -6 -4 -2 0 2 4 6 8 10 y = – 0,5 x (verde) y = –
0,3 x (rojo) y = – 0,1 x (azul) Funciones matemáticas -6
-8 -10

8 6 4 2 -2 40 Función lineal: y = a x + b ; para: 0 > a
> – 8 (siempre negativo) y b = 0 10 y = – 0,1 x (azul) y = –
0,3 x y = – 0,5 x Y = – 0,8 x (rojo) (verde) (violeta) Y ahora
tenemos todo el haz de rectas con “a” negativo. y=-1x
(celeste) -10 -8 -6 -4 -2 0 0 2 4 6 8 10 y = – 1,5 x (naranja) y=
-3x ( azul) -4 y = – 10 x y = – 100 x (rojo) (verde) Funciones
matemáticas -6 -8 -10

