
1 Movimientos vibratorios Movimiento vibratorio Armónico
Simple(MAS) Otros movimientos vibratorios Ecuaciones del MAS
Oscilador armónico simple Dinámica del oscilador
armónico simple Comparación del MAS y del MCU
Péndulo simple Energía del oscilador
armónico simple MOVIMIENTOS VIBRATORIOS Este enlace nos
lleva a una página del proyecto Newton del CNICE
(Ministerio de Educación) donde podemos ver esta unidad
completa con “escenas interactivas” (applets o
fislets) (animaciones)

2 1. Movimiento vibratorio armónico simple Movimiento
periódico Una partícula describe un movimiento
periódico cuando las variables posición, velocidad
y aceleración de ese movimiento toman los mismos valores
después de cada intervalo de tiempo constante llamado
periódo. El movimiento circular y uniforme MCU es un
ejemplo de movimiento periódico. En la figura la
partícula se desplaza siguiendo una trayectoria circular
con velocidad angular ? constante Cuando pasa por los puntos A,
B, C , ….. la posición , la velocidad lineal y la
aceleración tienen el mismo valor que en la vuelta
anterior A B C El movimiento de la luna alrededor de la Tierra,
el de la Tierra alrededor del Sol, el de las alas de un
pájaro cuando está volando, el de las mareas, el de
un péndulo, el de un objeto colgado de un muelle, etc son
ejemplos de movimientos periódicos.

3 Movimiento Oscilatorio o Vibratorio Son aquellos movimientos
periódicos en los que la partícula se desplaza
sucesivamente a un lado y a otro de una posición de
equilibrio. Cada vez que la partícula vuelve a la
posición de partida moviéndose en el mismo sentido
decimos que ha efectuado una oscilación y ha invertido un
tiempo que se llama periodo Cuando las oscilaciones son muy
rápidas se denominan vibraciones y al movimiento se le
denomina vibratorio. Movimiento Vibratorio Armónico Simple
(MAS) Un movimiento oscilatorio (o vibratorio) de una
partícula sobre una trayectoria rectilínea es
armónico simple cuando está sometido a la
acción de una fuerza de atracción directamente
proporcional al desplazamiento de la partícula de su
posición de equilibrio y de signo contrario. Las
partículas unidas a resortes (muelles) que cumplen la ley
de Hooke tienen un movimiento vibratorio armónico simple.
VER

4 1.1. Ecuaciones del movimiento vibratorio armónico
simple Como todo movimiento, para describir el MAS debemos
obtener unas ecuaciones que nos permitan conocer la
posición , la velocidad y la aceleración de una
partícula en un instante determinado. Cuando
estudiábamos el movimiento uniforme o el uniformemente
acelerado o el circular uniforme, vimos que para la
descripción de estos movimientos necesitábamos unas
ecuaciones para conocer la posición, la velocidad y la
aceleración de los cuerpo o partículas afectados
por estos movimientos: M.U. M.U.A. M.C.U. Pero antes, debemos
recordar o definir algunas magnitudes características de
este movimiento. (Gp:) x (Gp:) t (Gp:) v (Gp:) t (Gp:) x (Gp:)
t

5 1.1. Ecuaciones del MAS (Cont.) Oscilación o
Vibración es el movimiento comprendido entre el paso
consecutivo de la partícula por un mismo punto, con las
mismas características cinemáticas (igual
posición, igual velocidad e igual aceleración
Centro de Oscilación es el punto medio de la distancia que
separa las dos posiciones extremas alcanzadas por la
partícula. Es la posición de equilibrio.
Elongación es la posición que tiene la
partícula en un instante cualquiera, respecto del centro
de oscilación. En el S.I. se mide en m Amplitud A es la
máxima elongación. Representa la máxima
distancia que se aleja la partícula respecto del centro de
oscilación. En el S.I. se mide en m Periodo T es el tiempo
que tarda la partícula en efectuar una oscilación.
En el S.I. se mide en s Frecuencia f es el número de
oscilaciones que efectúa la partícula en la unidad
de tiempo. En el S.I. se mide en Hertzios (Hz) o s –1. La
representaremos por x o y según sea horizontal o vertical
la trayectoria rectilínea que describe la partícula
Es la inversa del periodo: -5 -4 -3 -2 -1 1 2 3 4 5

6 1.1. Ecuaciones del MAS (Cont.) Oscilación o
Vibración Centro de Oscilación Elongación
Amplitud A Periodo T Frecuencia f Pulsación ? es el
número de periodos comprendidos en 2 p segundos. En el
S.I. se mide en rad/s o s –1. Por definición: -5 -4
-3 -2 -1 1 2 3 4 5

7 Actividad El periodo de un movimiento vibratorio
armónico simple (MAS) es 0,2 s. Por definición:
Calcular su frecuencia y su pulsación. Datos: T = 0,2 s
Actividad El punto rojo de la figura realiza un MAS de 0,4 Hz de
frecuencia. Calcular: a) la pulsación , b) el periodo , c)
la amplitud en el S.I. -5 -4 -3 -2 -1 1 2 3 4 5 cm Datos: f =
0,40 Hz a) Por definición: c) Leemos el valor en la
figura: A = 5 cm = 0,05 m b) El periodo es el inverso de la
frecuencia:

8 1.1. Ecuaciones del MAS (Cont.) . Ecuación de la
elongación La ecuación fundamental del MAS nos
describe cómo varía la elongación x a lo
largo de la trayectoria en función del tiempo t.
Elongación (m) Amplitud (m) Ángulo de fase o fase
(rad) Fase inicial o constante de fase (rad) Ver RADIÁN
Una partícula posee un MOVIMIENTO ARMÓNICO SIMPLE a
lo largo de un eje X cuando su elongación o coordenada de
posición x sobre este eje se expresa mediante una
función senoidal o cosenoidal (seno o coseno) del tiempo
dado. ( Eje Y ) ( Condiciones iniciales) -5 -4 -3 -2 -1 1 2 3 4 5
Otras formas de la misma ecuación:

9 1.1. Ecuaciones del MAS (Cont.). Ecuación de la
elongación –1 0 = 0 0 0 +1 +A 0 0 0 0 –A T
Vamos a representar la gráfica x-t de este movimiento:
Elaboraremos una tabla de valores para obtener la gráfica.
x (m) t (s) 0 T (Gp:) +A (Gp:) – A 0 La ecuación de
la elongación también la podemos poner en
función de la frecuencia: En función del periodo la
ecuación es: 0
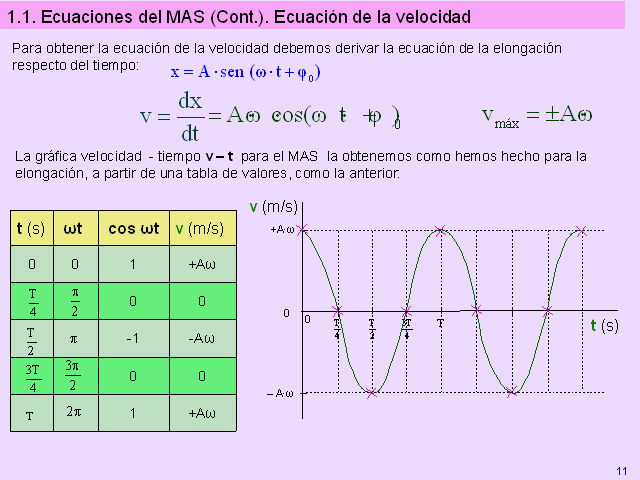
10 1.1. Ecuaciones del MAS (Cont.). Ecuación de la
velocidad Para obtener la ecuación de la velocidad debemos
derivar la ecuación de la elongación respecto del
tiempo: La gráfica velocidad – tiempo v – t para el
MAS la obtenemos como hemos hecho para la elongación, a
partir de una tabla de valores, como la anterior: v (m/s) t (s) 0
T (Gp:) +A·? (Gp:) – A·? 0 T

11 1.1. Ecuaciones del MAS (Cont.). Ecuación de la
aceleración Para obtener la ecuación de la
aceleración debemos derivar la ecuación de la
velocidad respecto del tiempo: La gráfica
aceleración – tiempo a – t para el MAS la obtenemos
como hemos hecho para la elongación y para la velocidad, a
partir de una tabla de valores, que tiene los mismos valores para
el sen ?t que la tabla de la elongación x: a (m/s2) t (s)
0 T (Gp:) +A·?2 (Gp:) – A·?2 0 T

12 1.2. Comparación del MAS y del MCU Para la mejor
comprensión del MAS de una partícula es útil
compararlo con el MCU de la misma partícula. APPLET
Proyecto Newton Vemos pues que el MAS se puede considerar como
una proyección de un MCU sobre un diámetro de la
misma circunferencia. -5 -4 -3 -2 -1 1 2 3 4 5 • Cada
revolución en el MCU se convierte en una oscilación
en el MAS • El radio R • El periodo T del MAS • La
velocidad angular ? • El ángulo inicial f0 del MCU
• El periodo T • La pulsación ? • La fase
inicial f0 son • La amplitud A • La proyección
del vector velocidad del MCU sobre el diámetro da lugar al
vector velocidad del MAS • La proyección del vector
aceleración normal del MCU sobre el diámetro da
lugar al vector aceleración del MAS

13 ?El Movimiento Armónico Simple es un movimiento
periódico en el que la posición varía
según una ecuación de tipo senoidal o cosenoidal.
?La velocidad del cuerpo cambia continuamente, siendo
máxima en el centro de la trayectoria y nula en los
extremos, donde el cuerpo cambia el sentido del movimiento. ?El
M.A.S. es un movimiento acelerado no uniformemente. Su
aceleración es proporcional al desplazamiento y de signo
opuesto a este. Toma su valor máximo en los extremos de la
trayectoria, mientras que es mínimo en el centro. ?Podemos
imaginar un M.A.S. como una proyección de un Movimiento
Circular Uniforme. El desfase nos indica la posición del
cuerpo en el instante inicial. Resumiendo

14 Ejercicio 6 de la página 102 Datos: MAS con 15
vibraciones cada 40 s a) La frecuencia f es el número de
vibraciones que da la partícula en la unidad de tiempo,
1s, luego: b) El período T , tiempo que tarda la
partícula en dar una vibración, es la inversa de la
frecuencia f : c) La pulsación ? la calculamos mediante la
expresión: También hemos podido utilizar la
expresión:

15 Actividad 1: Una partícula se mueve con un MAS cuya
elongación es: a) Calcular su amplitud: Comparamos la
ecuación que nos dan con la ecuación general de la
elongación del MAS. Deducimos por tanto que la amplitud
vale 0,8 m: b) Calcular su periodo: Podemos calcular el periodo T
a partir de la pulsación ? , ya que : Comparamos de nuevo
la ecuación que nos dan con la ecuación general de
la elongación del MAS. Deducimos por tanto que la
pulsación vale : ? = Calculamos el periodo T
despejándolo de la expresión anterior: c) Calcular
la fase inicial: Comparamos de nuevo la ecuación que nos
dan con la ecuación general de la elongación del
MAS. Deducimos por tanto que la fase inicial vale :

16 Actividad (Cont.) d) Calcular la elongación en los
instantes t = 0 s , t = 0,5 s y t = 1,5 s Para calcular la
elongación en esos instantes sustituiremos en la
ecuación la variable t por los valores que nos dan: Para t
= 0 s: Para t = 0,5 s: Para t = 1,5 s: e) Escribir la
ecuación de la velocidad. La ecuación de la
velocidad la obtenemos derivando respecto el tiempo la
ecuación de la elongación: f) ¿Cuál
es la velocidad máxima? El valor máximo de la
velocidad lo tomará cuando el cos(p t + p/6) sea 1. Por
tanto:

17 Actividad 2: Una partícula describe un MAS de
ecuación ( en unidades SI): Calcular cuánto vale la
velocidad de la partícula en los instantes que pasa por la
posición x = 3 m Datos: MAS ; ; x = 3 m La velocidad de la
partícula nos viene dada por la ecuación : Vemos
que depende del tiempo. Luego para calcular la velocidad cuando
la partícula pasa por la posición x = 3 m ,
bastaría con conocer el instante en el que la
partícula pasa por esa posición. Esto lo podemos
calcular a partir de la ecuación de la elongación:
Despejamos el seno: Calculamos el ángulo y el tiempo:
Finalmente, sustituimos este valor en la ecuación de la
velocidad:

18 Ejercicio 7 de la página 102 Datos: MAS , fo = 0 ; f =
50 Hz ; A = 3 cm = 0,03 m a) El período T, tiempo que
tarda la partícula en dar una vibración, es la
inversa de la frecuencia f : b) La pulsación ? la
calculamos mediante la expresión: c) La ecuación de
la elongación x en el MAS es: x = A· sen
(?·t + fo) y por tanto basta con conocer la amplitud A, la
pulsación ? y la fase inicial f0 : A = 0,03 m ? = 100 p
rad/s f0 = 0 rad x = 0,03· sen (100p·t + 0) x =
0,03· sen 100p·t en unidades del S.I. ( x =
0,03· sen 314,16·t en unidades del S.I. )

19 2.Oscilador armónico simple Hasta ahora hemos estudiado
las características cinemáticas del MAS. A
continuación vamos a estudiar la dinámica y la
energía del MAS, aplicadas a un caso concreto de oscilador
armónico (sistema animado de MAS debido a la acción
de una fuerza recuperadora ) 2.1. Dinámica del Oscilador
armónico simple Si una partícula de masa m
está sometida a un MAS hemos visto que tiene una
aceleración: Conocida la masa y la aceleración,
podemos a partir de la 2ª ley de Newton determinar la fuerza
resultante F sobre la partícula: Como la pulsación
? y la masa m son constantes, podemos concluir que: donde k es
una constante, denominada constante elástica o
recuperadora , que en el S.I. se mide en Vimos que en el MAS, la
fuerza responsable es directamente proporcional a la
elongación (al desplazamiento) de la partícula y
opuesta a ella . y a una fuerza:

20 2.1. Dinámica del Oscilador armónico simple
(Cont.) La fuerza que produce un MAS es una fuerza central,
dirigida hacia el punto de equilibrio y directamente proporcional
a la distancia a éste. Podemos calcular la
pulsación ? del MAS a partir de la expresión de la
constante: despejándo obtenemos que: Recordando que la
pulsación ? la podemos poner en función del periodo
T: podemos obtener el periodo T de oscilación de una
partícula producido por una fuerza recuperadora: Se
observa que el periodo y la frecuencia dependen exclusivamente de
la constante elástica del movimiento k y de la masa m del
cuerpo que lo describe.

21 2.2. Energía del Oscilador armónico simple Hemos
visto que un oscilador armónico es un sistema material que
se mueve con movimiento armónico simple MAS. La
energía mecánica que posee es CINÉTICA,
porque está en movimiento y POTENCIAL ELÁSTICA, ya
que el movimiento armónico es consecuencia de la
acción de una fuerza conservativa (la fuerza
elástica recuperadora). Energía cinética La
partícula de masa m que se mueve con una velocidad v
tendrá una energía cinética: Recordando la
ecuación de la velocidad y la expresión de la
constante k:

22 2.2. Energía del Oscilador armónico simple
(Cont.) Energía potencial elástica Para un
oscilador cuya constante elástica es k, la energía
potencial elástica en el instante que su elongación
es x vale: Recordando la ecuación de la elongación
: podemos expresar la energía potencial elástica
del oscilador de esta manera: Energía mecánica Es
la suma de las dos anteriores: La energía mecánica
de un oscilador armónico es una constante
característica de éste directamente proporcional al
cuadrado de la amplitud.

23 Ejercicio 21 de la página 105 Datos: m = 2 kg; F = 8,0
N; x = 20 cm = 0,2 m; a) Hallamos la constante elástica k
a partir de la fuerza necesaria para alargarlo 20 cm, a partir de
la posición de equilibrio: F = k · x Despejando la
constante k : b) El período del MAS en función de
la masa y de la constante elástica vale:

24 Ejercicio 23 de la página 107 Datos: m = 2 kg; k = 65
N/m; A = 0,3 m; a) En el momento inicial toda la energía
mecánica del cuerpo es energía potencial
elástica , ya que x = A = 0,3 m. En esta posición
su energía potencial es máxima. b) La velocidad
máxima la alcanzará al pasar por la posición
de equilibrio, donde su energía potencial elástica
será nula y toda la energía mecánica
será energía cinética. Podemos pues
determinar la velocidad, despejando de la expresión de la
energía cinética: (Gp:) l0 (Gp:) xmax = 0,3 m (Gp:)
Posición de equilibrio

25 2.3. Péndulo simple Si suspendemos una pequeña
partícula material de masa m de un hilo de longitud L,
inextensible y de masa despreciable, y la separamos un
pequeño ángulo a de su posición vertical de
reposo, la partícula se comporta como un oscilador. Este
sistema recibe el nombre de péndulo simple o
matemático El movimiento del péndulo simple es un
movimiento armónico simple siempre que se consideren
desplazamientos (amplitudes) muy pequeños Con esa
aproximación, a partir de la ecuación del periodo
del MAS que vimos anteriormente podemos obtener una nueva
ecuación para el periodo del péndulo: Se observa
que el periodo del péndulo depende exclusivamente de la
longitud del hilo L y del valor de la aceleración de la
gravedad g del lugar donde éste oscila. Periodo del MAS
Periodo del péndulo (Gp:) L (Gp:) m (Gp:) a

26 Ejercicio 27 de la página 109 Datos: L = 0,556 m si g =
9,75 m/s2 ; gLuna = 1,96 m/s2 ; a) Aplicando la ecuación
del periodo del péndulo: b) Con los datos de la Tierra,
calculamos la longitud L del péndulo: Y una vez conocida
su longitud, ya podemos calcular su periodo en la Luna:

27 l0 l l l x x x x = l – l0 Ley de Hooke Los cuerpos
elásticos se deforman al aplicarles una fuerza,pero
¿qué relación existe entre la intensidad de
la fuerza recuperadora y la deformación producida ? El
físico inglés R.Hooke determinó en el siglo
XVII esta relación, lo que se conoce como ley de Hooke. La
deformación x que sufre un cuerpo elástico es
directamente proporcional a su fuerza recuperadora y de sentido
contrario . Matematicamente: F = – k · x siendo k la
constante de proporcionalidad, que recibe el nombre de CONSTANTE
ELÁSTICA F F F

28 RADIÁN R El radián es el ángulo central
de una circunferencia que abarca un arco igual al radio de la
circunferencia: Como la longitud total de la circunferencia es:
El ángulo completo de la circunferencia equivale a: La
equivalencia entre grados sexagesimales y radián es:
