ELEMENTOS DE TRIGONOMETRIA
1
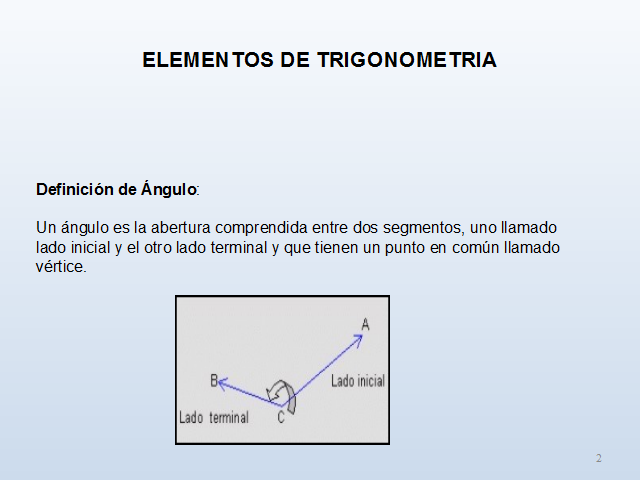
Definición de Ángulo:Un ángulo es la abertura comprendida entre dos segmentos, uno llamado lado inicial y el otro lado terminal y que tienen un punto en común llamado vértice.

ELEMENTOS DE TRIGONOMETRIA
2
Medición de ángulos:
Para el estudio de las funciones circulares, un ángulo además de medirse en los sistemas sexagesimal y centesimal se mide en el sistema de medida circular.Sistema sexagesimal:
La rotación total de una circunferencia corresponde a un ángulo de 360°. La unidad básica para la medición de ángulos en el sistema sexagesimal es el grado, que se define como parte de la rotación total:
Se tiene entonces que : 1° = 60´ y 1´= 60"

ELEMENTOS DE TRIGONOMETRIA
3
Sistema Centesimal:
En este sistema la unidad de medida es el grado centesimal.
El mismo se define como la centésima parte de un ángulo recto.
Es decir que :
1° = 1/100
Por lo tanto si dividimos al grado centesimal por 100 tendremos el minuto centesimal :1´ =1°/100
Y el segundo centesimal :
1”=1’/100

ELEMENTOS DE TRIGONOMETRIA
4
Sistema Circular
En este sistema la unidad de medida es el radian.
El radian se define como el ángulo en el cual la longitud del arco (s) es igual al radio (r):
Esta condición se da (r=s) cuando el ángulo subtendido por el arco en el sistema Sexagesimal es de 57,3°

ELEMENTOS DE TRIGONOMETRIA
5
Equivalencias entre los Sistemas de Medida
La pregunta que podríamos hacernos es cuantos radianes tiene un ángulo que rota 360° sexagesimales?
Entonces si dividimos 360 /57,3 ˜ 6.283
La mitad de este ángulo es lo que conocemos comúnmente como el Numero p˜3.1416
Por lo tanto 360°= 2p

ELEMENTOS DE TRIGONOMETRIA
6
Tenemos que p radianes es igual a 180°.
Y gracias a estos quebrados podremos obtener las siguientes equivalencias:

ELEMENTOS DE TRIGONOMETRIA
7
A b C
c a
B
C
A=90º
Hipotenusa
B
En todo triángulo rectángulo, con independencia de las medidas de sus lados (catetos e hipotenusa) hay unas relaciones entre sus lados que se cumplen siempre, y que sólo dependen del valor de los ángulos agudos del triángulo.

ELEMENTOS DE TRIGONOMETRIA
8
?= L/R ; R=1
?= L/1 ; ?=L
(solo se cumple numéricamente)
“Es decir que el numero de radianes del ángulo central es igual a la longitud del arco pero solo como arco numérico”

ELEMENTOS DE TRIGONOMETRIA
9
La circunferencia goniométrica (trigonométrica o unitaria) es una herramienta muy útil a la hora de visualizar y definir razones trigonométricas de ángulos cualesquiera.
Se trata de una circunferencia de radio 1, situada en el origen de coordenadas. En ella se dibujan los ángulos de la siguiente forma:
El vértice en el origen de coordenadas.
Uno de sus lados en el eje de las x.
El otro lado se sitúa con la amplitud deseada: se mide el ángulo en sentido contrario a las agujas del reloj.
La circunferencia goniométrica se divide en cuatro partes, denominadas cada una de ellas cuadrantes. Los cuadrantes se numeran a partir del semieje positivo de las x, en sentido antihorario: primero, segundo, tercero y cuarto:

ELEMENTOS DE TRIGONOMETRIA
10

ELEMENTOS DE TRIGONOMETRIA
11
La parte del plano comprendida entre el semieje positivo de las x y el semieje positivo de las y es el primer cuadrante.
La parte del plano comprendida entre el semieje positivo de las y, y el semieje negativo de las x es el segundo cuadrante
Y así sucesivamente. Tomando en cuenta los ángulos de la figura adjunta tenemos:
Primer cuadrante: de 0 a 90º, x>0, y >0
Segundo cuadrante: de 90 a 180º, x< 0, y>0
Tercer cuadrante: de 180º a 270º, x< 0, y< 0
Cuarto cuadrante: de 270º a 360º, x>0, y< 0
Dependiendo del cuadrante considerado, las funciones trigonométricas seno, coseno y tangente tienen un valor positivo o negativo.

ELEMENTOS DE TRIGONOMETRIA
12
Relaciones trigonométricas: seno
Se representa por la perpendicular trazada desde el extremo del arco, hacia el diámetro horizontal:
En el ? OQP: sen?= QP/OP= Y/1
. Sen? = y
* De la figura:
Página siguiente  |