Interpolación y aproximación de Funciones

2. Contenido
3. Lenguaje
   utilizado
4. Páginas Web
   consultadas
5. Bibliografía
   consultada

Introducción:

La interpolación y la aproximación de
funciones se
aplican en la informática en diversos campos:

Tratamientos de imágenes
mediante una animación interpolada:

La animación se crea mediante el cambio del
contenido de imágenes sucesivas. Puede hacer que un objeto
se desplace, aumente o disminuya de tamaño, gire, cambie
de color, aparezca o
desaparezca, o cambie de forma. Los cambios pueden ocurrir por
separado o combinados entre sí.

• Interpolación de movimiento, se definen
  propiedades como la posición, el tamaño y la
  rotación de una instancia, un grupo o un
  bloque de tipos en un punto en el tiempo, y estas
  propiedades se cambian en otro punto.
• Interpolación de forma: se dibuja una
  forma en un punto del tiempo y se cambia o se dibuja una nueva
  en otro punto. Al interpolar formas se crea un efecto similar
  al de transformación y las formas parecen cambiar en el
  transcurso del tiempo.

La animación interpolada es una forma eficaz de
crear movimiento y
cambios a lo largo del tiempo y de reducir al mínimo el
tamaño del archivo. Al
contrario de la animación imagen a imagen,
sólo necesita almacenar los valores de
los cambios de la imagen, no la imagen completa.

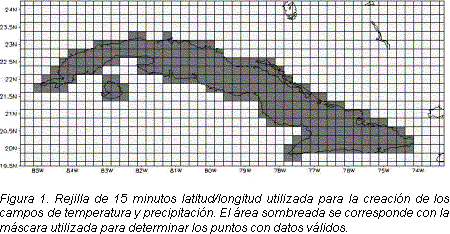
Mediciones de temperaturas y
precipitaciones

Los datos iniciales
utilizados en este trabajo son las medias mensuales de temperatura
(máxima, mínima y media) y precipitaciones. Para
realizar la interpolación de los valores de las
estaciones hacia una rejilla de 15 minutos latitud/longitud
(Figura 1), se utilizó un Sistema de
Visualización y Análisis en Rejilla (GrADS), un software desarrollado por el
Centro para Estudios del sistema Tierra-Océano-Atmósfera de la
Universidad de
Maryland de los Estados Unidos.
El esquema de interpolación incorporado en GrADS es el
método de
Cressman, el cual ha sido ampliamente utilizado en aplicaciones
de la meteorología.

La disminución del número de estaciones
reduce la calidad de las
interpolaciones y esta variación en el número de
puntos puede introducir movimientos irreales en las series
temporales de los campos generados, con independencia
del método de interpolación que se utilice;
así los campos interpolados con menos estaciones no
serán capaces de captar todas las características espaciales del
fenómeno. Este inconveniente hizo necesario que se
utilizara una estrategia para
garantizar que los campos de temperatura y precipitación
interpolados, pudieran representar las características
espaciales y temporales de ambas variables
durante todo el período considerado. De esta forma las
series de tiempo en rejilla se estimaron utilizando el
método propuesto por Willmott y Robeson (1995). Este
método, denominado por esos autores como
Interpolación Climatológicamente Asistida (ICA),
parte de la idea de realizar la interpolación, separando
las componentes espaciales y temporales.

Tratamiento de imágenes:

La interpolación es el método por el que
se calculan más puntos de muestra, de
acuerdo con un algoritmo del
software de imágenes –programa de
escaneado, para compensar las limitaciones de la
resolución óptica.
Por lo tanto, si la resolución óptica es de 1000
dpi, la interpolación sólo se utilizará si
resoluciones mayores de 1000 dpi se requieren. Esto es
especialmente útil al escalar imágenes para
erradicar trazos que no se quieren y que parecen como efectos de
eslabones en los contornos de la imagen.

Por ejemplo, para escanear a 600 dpi una fotografía
y doblar el tamaño de salida de la imagen sin perder
detalles, la imagen tiene que contener el mismo nivel de detalles
que la fotografía original. Si la imagen se aumenta sin
interpolación, el espacio entre los puntos o las
líneas será doblado. Esto significa que el mismo
números de puntos se tendrán que situar en un
área dos veces mayor dando a la imagen una calidad
granulada inconsistente. Con la interpolación, la densidad de la
imagen se preservara introduciendo el número de puntos que
se requieran en el espacio abierto, dando así a la imagen
resultante una mejor calidad. La interpolación se realiza
durante los procesos tanto
de reducción como de aumento.

Reconstrucción de una señal a partir de
sus muestras usando interpolación:

La interpolación es un proceso de
empleo
común en la reconstrucción aproximada o exacta de
una señal a partir de sus muestras. Para una señal
de banda limitada, si los instantes de muestreo
están bastante cerca, entonces la señal puede
reconstruirse exactamente, es decir, mediante el empleo de un
filtro se puede efectuar la interpolación exacta entre los
puntos de muestreo. La interpretación de la
reconstrucción de una señal como un proceso de
interpolación se hace evidente cuando se considera el
efecto en el dominio del
tiempo del filtro.

La utilización de la interpolación como
una técnica tiene un amplio espectro de utilización
tanto es así que es reformulada en cada campo que aplica.
La interpolación también es usada en:

Topografías, tecnologías de comunicación, genética,
biotecnologías, reconstrucción tridimensional de
imágenes medicas, etc.

Contenido:

Este manual cumple con
el objetivo de
enseñar la instalación y utilización del
lenguaje PDL –
Perl data Language – en su versión 2.3.4, utilizando la
interpretación de PERL con el paquete ActivePerl
versión 5.8.0.805.

Partiendo desde una base teórica se intenta
familiarizar a el usuario con los conceptos fundamentales para su
desarrollo. Se
hace referencia de como utilizar los comandos para
solucionar un determinado problema, además se incluyen
ejemplo de su resolución, así como también
de la puesta en marcha de los mismos.

Requerimientos Mínimos

Nota:

Los siguientes componentes mencionados deben estar
presentes en el equipo:

* Perl versión 5.6.1

* Perl ISAPI: Compatible con

servidores Web IIS 4.0+
o

PWS 4.0+

* PerlScript: ActiveX scripting host

como IE 4.0+, o Windows

Scripting Host

* Windows 95: DCOM
para Windows 95

* Windows NT:
Service Pack 5+ y Windows Installer

1.1+

* Espacio disponible en disco: aproximadamente 55 Mb
para la instalación típica.

En todas las versiones Windows debe estar presente
Windows Installer 2.0+

Lenguaje utilizado

1.1 .- Conocimientos
Básicos

PDL es un lenguaje de
programación orientado tratamiento numérico de
datos. Sus siglas significan Perl Data Language, y como su nombre
indica está basado en el lenguaje de
programación Perl, esto quiere decir que es
un modulo del programa, por lo tanto es necesario tenerlo ya
instalado a la hora de colocar PDL. Perl es gratuito y
además es Software Libre, esto quiere decir que el
código
fuente está disponible para que cualquiera lo pueda ver o
modificar.

Perl es la abreviación de Practical Extraction
and Report Language. Es lo que se conoce como un lenguaje script,
es decir, uno en el que no hace falta compilar el programa
escrito.

El fuerte de PDL es la posibilidad de manipular matrices
n-dimensionales y además de poder resolver
cálculos numéricos matriciales de una forma
rápida.

Una de las características centrales de PDL es
poder relacionarse fácilmente con el sistemas.

Tal como hemos mencionado, PDL es un lenguaje de
cálculo
numérico basado en Perl Está disponible en
múltiples plataformas y sistemas
operativos. De hecho funciona en diferentes versiones de
Unix, Linux y todo tipo
de Windows. Un programa que se escriba teniendo en cuenta la
compatibilidad puede ser escrito en una plataforma y ejecutado en
otra.

Se pueden conseguir el modulo para cálculo
numérico de PDL y otros a través de el CPAN
-Comprehensive Perl Archive Network.

El proyecto PerlDL
apunta a convertir Perl en un eficiente lenguaje numérico
para computadoras.
El modulo PDL le da al Perl estándar la habilidad de
manipular rápidamente y guardar compactamente matrices de
N-dimensiones. Uno puede escribir expresiones simples en PERL y
manipular cadenas numéricas enteras todo de una sola
vez.

PDL convierte a PERL en un lenguaje numérico
gratuito similar al paquete comercial MATLAB.

Con el paquete es provisto un SHELL llamado PERLDL el
cual se usa en la líneas de comando y un modulo llamado
PDL para el uso en los SCRIPT de PERL.

La distribución PDL para PERL es gratuita y
proporciona una amplia funcionalidad numérica con soporte
para visualización de dos y tres dimensiones, así
también como una gran variedad de rutinas de
entrada/salida. El objetivo de PDL es permitir una interactividad
con una gran variedad de paquetes numéricos, gráficos y de sistemas de
visualización.

A continuación se proporcionará una breve
reseña sobre el manejo de operadores relacionales y
lógicos, así como también de las funciones
que competen al lenguaje.

1.2 .- Instalación en Linux /
Unix

Puedes utilizar el modulo CPAN de Andreas König
para que automáticamente ejecute los procesos de
descompresión y instalación.

1.2.1 .- Instalación de archivos
comprimidos

tar.gz

A)- Descompresión

Descomprimir el archivo con

gzip -d moduloPDL.tar.gz

Puedes obtener el descompresor gzip de

ftp://prep.ai.mit.edu/pub/gnu.

O puedes combinar este paso con el

siguiente para guardar en disco

gzip -dc moduloPDL.tar.gz | tar -xof

B)- DESEMPAQUETANDO

Desempaquetar el resultado con

tar -xof moduloPDL.tar

C)- COMPILANDO

Entrar en el directorio nuevo y escribir:

perl Makefile.PL

make

make test

D)- INSTALANDO

Sin salir del directorio, escribimos:

make install

Asegurese de tener los permisos apropiados para instalar
en el directorio de la librería de PERL. Después
necesitara ser el root.

Esto es todo lo que necesitas hacer con las conexiones
dinámicas.

Muchos sistemas Unix tienen conexiones dinámicas,
si usted no las tiene o si por cualquier razón tiene
conexiones estáticas en PERL, y el modulo requiere
ser

compilado, usted necesitara una versión binaria
que incluya el modulo. De nuevo usted necesitara ser el
root

1.2.2 .- Instalando los paquetes RPM

Instalación del paquete Perl

rpm –install -nodeps
ActivePerl-5.8.0.805-i686-linux.rpm

Instalación del paquete MESA

rpm –install -nodeps Mesa-3.4-13.i386.rpm

Instalación dl paquete PGPLOT

rpm –install -nodeps
pgplot-5.2.0-2.i386.rpm

Instalación del paquete OPENGL

rpm –install -nodeps
oss-opengl-glu-20000925-1.i386.rpm

Instalación del paquete PDL

rpm –install -nodeps pdl-2.2.3-1.i386.rpm

Compilación / instalación de
PDL

Utilizar los pasos de compilación e
instalación anteriormente ya descriptos (sección
1.2 Instalación de archivos comprimidos tar.gz)

1.3 .- Instalación en Windows

Descomprimir el archivo

Usar el manejador de paquetes para instalar
PDL:

ppm install –localización=. PDL

Los documentación de PDL en HTML son
instalados en el directorio html. Casi siempre debido a un
defecto del la versión actual del manejador de paquetes
(ppm), no son reflejados en el índice de la
documentación de perl. Por favor copia en el directorio
html/lib/pdl los archivos. Las referencias cruzadas en el los
archivos html son actualmente borradas. El script de post
instalación es necesario par corregir esto en el
futuro.

Ante cualquier consulta dirigirse a:

pdl-porters[arroba]jach.hawaii.edu

Interpolación de funciones

Los valores de las funciones polinomiales se pueden
determinar efectuando un numero finito de sumas y
multiplicaciones. Sin embargo, existen otras funciones, tales
como la logarítmica, la exponencial y las funciones
trigonométricas , que no se pueden evaluar tan
fácilmente. En esta sección demostraremos que
muchas funciones se pueden calcular en forma aproximada por
polinomios y que puede usarse el polinomio en vez de la
función original, para los cálculos, cuando la
diferencia entre los valores de la función y la
aproximación polinomial es suficiente
pequeña.

 Interpolación

Para ver el gráfico seleccione la
opción
"Descargar" 

1 .- Polinomio de interpolación de
diferencias divididas de Newton

1.1 .- Interpolación
lineal:

1.1.1 .- Enunciado
Teórico:

Teniendo dos puntos como datos X0 ^
X1 la interpolación lineal consiste en
conectarlos con un polinomio de primer orden (una
recta)

f1 (x) = f(x0) + f(x1)
– f(x0) * (x – x0)

x1 – x0

f1 (x) = b0 + b1 (x –
x0)

Antes de explicar la interpretación
geométrica, comenzaremos resolviendo un
ejemplo:

Ejemplo1:

Se quiere aproximar f(x) = sen x en el intervalo
[0,∏], con:

Calcule sen 1 con cada una de las curvas
encontradas y compare con el valor verdadero.

1.1.2 .- Interpretación
geométrica

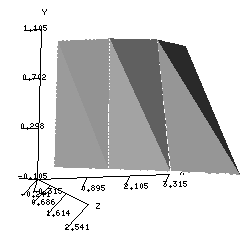
Figura 1: Interpretación grafica
del resultado de la función a evaluar.

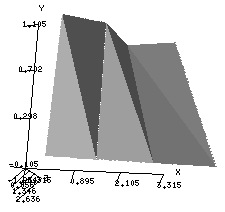
Figura 2: Interpretación grafica
de la interpolación lineal de Newton

.

Figura 3: Interpretación grafica
de la función a evaluar ( f(x)=sen x ).

1.1.3 .- Código Fuente

# EJEMPLO 1 – INTERPOLACION LINEAL DE NEWTON

use PDL;

use PDL::Graphics::TriD;

#defino los valores iniciales

print "nn Inserte un numero perteneciente al intervalo
: ";

$coeficiente = <STDIN>;

print "n Ingrese el primer numero: ";

$x0 = <STDIN>;

print "n Ingrese el segundo numero: ";

$x1 = <STDIN>;

print "n Ingrese el tercer numero: ";

$x2 = <STDIN>;

print "n Ingrese el cuarto numero: ";

$x3 = <STDIN>;

#calculo las funciones

$resultado = pdl([ [$x0,$x1,$x2,$x3], [sin $x0,sin
$x1,sin $x2, sin $x3] ]);

$original = zeroes(50,50)->xlinvals(-4,4);

#calculo la función aproximada

$f1= sin $x0 + ((sin $x1-sin
$x0)/($x1-$x0))*($coeficiente-$x0);

$f2= sin $x1 + ((sin $x2-sin
$x1)/($x2-$x1))*($coeficiente-$x1);

$f3= sin $x2 + ((sin $x3-sin
$x2)/($x3-$x2))*($coeficiente-$x2);

$aproximado = pdl([ [0,0.7,1.5,2.3], [$f1,$f2,$f3]
]);

print "nn";

print "La matriz resultante es: n";

print $resultado;

print "n n";

print "Cuando aparezcan las graficas
presionar la TECLA Q para pasar a la siguiente nn";

print " 1 – Resultado del intervalo n";

print " 2 – Resultado Aproximado del
intervalon";

print " 3 – Función Original n";

print " n";

print "Presione ENTER para continuar …";

<STDIN>;

imag3d ([$resultado]);

imag3d ([$aproximado]);

imag3d ([sin $original]);

hold();

1.2 .- Interpolación
cuadrática:

1.2.1 .- Enunciado
Teórico:

Teniendo tres puntos como datos X0,
X1 ^ X2. La interpolación
cuadrática consiste en conectarlo con en polinomio de
segundo orden (una parábola) de la siguiente
manera:

f2 (x) = b0 + b1 (x
– x0) + b2 (x –
x1)

b0 = f(x0) b1 =
f(x1) – f(x0)

x1 – x0

f(x2) – f(x1) –
f(x1) – f(x0)

b2 = x2 – x1
x1 – x0

x2 – x0

1.2.2 .- Interpretación
geométrica

Como resolvemos el ejemplo 1 por interpolación
cuadrática de Newton
entonces las figuras 1 y 3 se mantienen constantes.

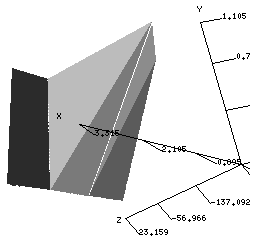
Figura 4: Interpretación grafica
de la interpolación cuadrática de Newton

1.2.3 .- Código Fuente

# EJEMPLO 2 – INTERPOLACION CUADRATICA DE
NEWTON

use PDL;

use PDL::Graphics::TriD;

#defino los valores iniciales

print "nn Inserte un numero perteneciente al intervalo
: ";

$x = <STDIN>;

print "n Ingrese el primer numero: ";

$x0 = <STDIN>;

print "n Ingrese el segundo numero: ";

$x1 = <STDIN>;

print "n Ingrese el tercer numero: ";

$x2 = <STDIN>;

print "n Ingrese el cuarto numero: ";

$x3 = <STDIN>;

#calculo las funciones

$resultado = pdl([ [$x0,$x1,$x2,$x3], [sin $x0,sin
$x1,sin $x2, sin $x3] ]);

$original = zeroes(50,50)->xlinvals(-4,4);

#calculo la función aproximada

#calculo f0(x)

$b0 = sin $x0;

$b1 = (sin $x1 – sin $x0) / ($x1-$x0);

$b2 = ((sin $x2 – sin $x1) – (sin $x1 – sin
$x0))/($x2-$x0);

$f0 = $b0 + ($b1*($x – $x0)) + ($b2 * ($x – $x0) * ($x –
$x1));

#calculo f1(x)

$b0 = sin $x1;

$b1 = (sin $x2 – sin $x1) / ($x2-$x1);

$b2 = ((sin $x3 – sin $x2) – (sin $x2 – sin
$x1))/($x3-$x1);

$f1 = $b0 + ($b1*($x – $x1)) + ($b2 * ($x – $x1) * ($x –
$x2));

$aproximado = pdl([ [0,0.7,1.5,2.3], [$f0,$f1]
]);

print "nn";

print "La matriz resultante es: n";

print $resultado;

print "n n";

print "Cuando aparezcan las graficas presionar la TECLA
Q para pasar a la siguiente nn";

print " 1 – Resultado del intervalo n";

print " 2 – Resultado Aproximado del
intervalon";

print " 3 – Función Original n";

print " n";

print "Presione ENTER para continuar …";

<STDIN>;

imag3d ([$resultado]);

imag3d ([$aproximado]);

imag3d ([sin $original]);

hold();

2 .- Polinomio de interpolación de
Lagrange:

Es una reformulación del polinomio de Newton,
este polinomio de interpolación evita el cálculo de
las diferencias divididas y vine dado por:

2.1 .- Forma general:

 Para ver el
gráfico seleccione la opción
"Descargar"

  Este es el único polinomio de n-esimo
orden que pasa exactamente por los n + 1 puntos.

Si tenemos n=1 2 puntos  

2.2 .- Forma lineal:

2.2.1 .- Enunciado
Teórico:

f1 (x) = x – x1 f (x0)
+ x – x0 f (x1)

x0 – x1 x1 –
x0

l0 (x) = x – x1 l1
(x) = x – x0

x0 – x1 x1 –
x0

2.2.2 .- Interpretación
geométrica

Como resolvemos el ejemplo 1 por interpolación
lineal de lagrange entonces las figuras 1 y 3 se mantienen
constantes.

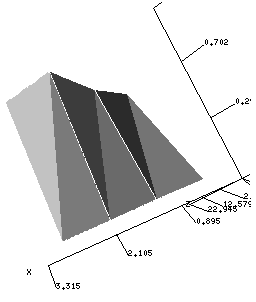
Figura 5: Interpretación grafica
de la interpolación lineal de Lagrange.

2.2.3 .- Código Fuente

# EJEMPLO 3 – INTERPOLACION LINEAL DE
LAGRANGE

use PDL;

use PDL::Graphics::TriD;

#defino los valores iniciales

print "nn Inserte un numero perteneciente al intervalo
: ";

$x = <STDIN>;

print "n Ingrese el primer numero: ";

$x0 = <STDIN>;

print "n Ingrese el segundo numero: ";

$x1 = <STDIN>;

print "n Ingrese el tercer numero: ";

$x2 = <STDIN>;

print "n Ingrese el cuarto numero: ";

$x3 = <STDIN>;

#calculo las funciones

$resultado = pdl([ [$x0,$x1,$x2,$x3], [sin $x0,sin
$x1,sin $x2, sin $x3] ]);

$original = zeroes(50,50)->xlinvals(-4,4);

#calculo la función aproximada

$f1 = (($x – $x1)/($x0 – $x1) * sin $x0) + (($x –
$x0)/($x1 – $x0) * sin $x1);

$f2 = (($x – $x2)/($x1 – $x2) * sin $x1) + (($x –
$x1)/($x2 – $x1) * sin $x2);

$f3 = (($x – $x3)/($x2 – $x3) * sin $x2) + (($x –
$x2)/($x3 – $x2) * sin $x3);

$aproximado = pdl([ [0,0.7,1.5,2.3], [$f1,$f2,$f3]
]);

print "nn";

print "La matriz resultante es: n";

print $resultado;

print "n n";

print "Cuando aparezcan las graficas presionar la TECLA
Q para pasar a la siguiente nn";

print " 1 – Resultado del intervalo n";

print " 2 – Resultado Aproximado del
intervalon";

print " 3 – Función Original n";

print " n";

print "Presione ENTER para continuar …";

<STDIN>;

imag3d ([$resultado]);

imag3d ([$aproximado]);

imag3d ([sin $original]);

hold();

2.3 .- Forma cuadrática:

2.3.1 .- Enunciado
Teórico:

Para ver el gráfico seleccione la
opción
"Descargar" 

2.3.2 .- Interpretación
geométrica

Como resolvemos el ejemplo 1 por interpolación
cuadrática de Lagrange entonces las figuras 1 y 3 se
mantienen constantes.

Figura 6: Interpretación grafica
de la interpolación cuadrática de
Lagrange

2.3.3 .- Código Fuente

# EJEMPLO 4 – INTERPOLACION CUADRATICA DE
LAGRANGE

use PDL;

use PDL::Graphics::TriD;

#defino los valores iniciales

print "nn Inserte un numero perteneciente al intervalo
: ";

$x = <STDIN>;

print "n Ingrese el primer numero: ";

$x0 = <STDIN>;

print "n Ingrese el segundo numero: ";

$x1 = <STDIN>;

print "n Ingrese el tercer numero: ";

$x2 = <STDIN>;

print "n Ingrese el cuarto numero: ";

$x3 = <STDIN>;

#calcuo las funciones

$resultado = pdl([ [$x0,$x1,$x2,$x3], [sin $x0,sin
$x1,sin $x2, sin $x3] ]);

$original = zeroes(50,50)->xlinvals(-4,4);

#calculo la función aproximada

$f1 = (((($x – $x1)*($x – $x2)) / (($x0 – $x1) *
($x0-$x2))) * sin $x0) + (( (($x – $x0)*($x – $x2)) / (($x1 –
$x0) * ($x1-$x2)) ) * sin $x1) + (( (($x – $x0)*($x – $x1)) /
(($x2 – $x0) * ($x2-$x1)) ) * sin $x2);

$f2 = (((($x – $x2)*($x – $x3)) / (($x1 – $x2) *
($x1-$x3))) * sin $x1) + (( (($x – $x1)*($x – $x3)) / (($x2 –
$x1) * ($x2-$x3)) ) * sin $x2) + (( (($x – $x1)*($x – $x2)) /
(($x3 – $x1) * ($x3-$x2)) ) * sin $x3);

$aproximado = pdl([ [0,0.7,1.5,2.3], [$f1,$f2]
]);

print "nn";

print "La matriz resultante es: n";

print $resultado;

print "n n";

print "Cuando aparezcan las graficas presionar la TECLA
Q para pasar a la siguiente nn";

print " 1 – Resultado del intervalo n";

print " 2 – Resultado Aproximado del
intervalon";

print " 3 – Función Original n";

print " n";

print "Presione ENTER para continuar …";

<STDIN>;

imag3d ([$resultado]);

imag3d ([$aproximado]);

imag3d ([sin $original]);

hold();

Paginas Web Consultadas:

Pagina Oficial:

• http://pdl.perl.org/

Lista de Archivos para descargar:

• http://sourceforge.net/project/showfiles.php?group_id=612

Paquete para la versión de Linux
Debian:

• http://packages.debian.org/pdl
• http://fink.sourceforge.net/pdb/package.php/pdl

Servidor CVS (cvsweb):

• http://cvs.sourceforge.net/cgi-bin/viewcvs.cgi/pdl/

Paginas relacionadas:

• http://glub.ehu.es/recursos–castellano/
  Linux_en_castellano-6.html
• http://www.perl.com
• http://aspn.activestate.com/ASPN/CodeDoc/PDL/Basic/Pod/Tips.html
• http://www.met.inf.cu/sometcuba/Boletin/v07_n01/art_abel04.htm
• http://www.servicios-graficos.com/home/Usuarios/Tutoriales/TeoCol/interpol/body_interpol.html
• http://www.mappinginteractivo.com/plantilla-ante.asp?id_articulo=128
• http://itzamna.uam.mx/pilar/rec_3d.html

Bibliografía
consultada

• "El calculo con geometría
  Analítica" – Luis Leithold – Sexta
  edición

Petersen Alberto Matías

pdl-porters[arroba]jach.hawaii.edu