Introducción, definición
y clasificación
de las vibraciones.
- Las vibraciones
mecánicas: historia, estudio e
importancia. - Las vibraciones mecánicas
definiciones, clasificaciones. - Elementos de sistemas
vibratorios - Vibración
libre - Métodos para el calculo de
ecuaciones diferenciales de sistemas libres no
amortiguados - Cálculo de momento de
inercia y centroides.
El estudio de las vibraciones
mecánicas se ha convertido en algo esencial para el
estudiante de ingeniería mecánica ya que el buen funcionamiento de
maquinaria mecánica esta relacionado en muchos casos
con su comportamiento
vibratorio.
Es importante conocer la clasificación de las
vibraciones mecánicas ya que nos presentan un panorama de
los diferentes estudios.
Otra herramienta importante en el estudio de las
vibraciones mecánicas es el modelo
matemático. Este procedimiento
debe ser preciso ya que los errores produce información errónea.
En este capitulo se verán los conceptos iniciales
importantes para el estudio de las vibraciones
mecánicas.
Desde que aparecieron los primeros instrumentos
musicales, en especial los de cuerda, la gente ya
mostraba un interés por el estudio del
fenómeno de las vibraciones, por ejemplo, Galileo
encontró la relación existente entre la
longitud de cuerda de un pendido y su frecuencia de
oscilación, además encontró la
relación entre la tensión, longitud y
frecuencia de vibración de las cuerdas.Estos estudios y otros posteriores ya indicaban la
relación que existe entre el sonido y
las vibraciones mecánicas.A través de la historia,
grandes matemáticos elaboraron importantes
aportaciones que hicieron del fenómeno de las
vibraciones toda una ciencia,
tan asi que hoy en día se ha convertido en una de
las mas estudiadas y aplicadas en la industria.Podemos mencionar entre otros, Taylor,
Vernoulli, D’ Alember, Lagrange, Fourier, etc. La
ley de
Hooke en 1876 sobre la elasticidad, Coulomb dedujo la teoria y la
experimentación de oscilaciones torcionales,
Rayleigh con su método de energías, etc.
Fueron grandes físicos que estructuraron las bases
de las vibraciones como ciencia.En la actualidad, las vibraciones mecánicas es el
fenómeno en el cual la gente esta en continuo
contacto y cuyos efectos difieren.El buen funcionamiento de los amortiguadores de un
automóvil. El mal aislamiento de maquinaria que
pueda dañar la infraestructura de la misma y zona
aledaña, ruido
causada por maquinaria. Son ejemplos de algunos
ejemplos.Un fenómeno de la cual las maquinas temen es la
llamada resonancia, cuyas consecuencias pueden ser
serias.Por otro lado el buen funcionamiento de la maquinaria
industrial es un fenómeno que requiere de una
constante inspección, es decir, el mantenimiento predictivo; este juega un
papel
importante en el crecimiento
económico de una
empresa, ya que predecir una falla es sinónimo
de programación de eventos
que permite a la
empresa decidir el momento adecuado para detener la
maquina y darle el mantenimiento.El análisis de vibración juega un
papel
importante en el mtto predictivo, este consiste en tomar
medida de vibración en diferentes partes de la
maquina y analizar su comportamiento.- LAS VIBRACIONES
MECANICAS: HISTORIA,
ESTUDIO E IMPORTANCIA. - LAS VIBRACIONES MECANICAS
DEFINICIONES, CLASIFICACIONES.
El estudio de las vibraciones
mecánicas también llamado, mecánica delas
vibraciones, es una rama de la mecánica, o mas
generalmente de la ciencia,
estudia los movimientos oscilatorios de los cuerpos o sistemas y de las
fuerzas asociadas con ella.
Definición 1.2 (a)
Vibración: es el movimiento de
vaiven que ejercen las partículas de un cuerpo debido a
una exitación.
Existe una relación entre el estudio de las vibraciones
mecánicas del sonido, si un
cuerpo sonoro vibra el sonido escuchado esta estrechamente
relacionado con la vibración mecánica, por ejemplo
una cuerda de guitarra vibra produciendo el tono correspondiente
al # de ciclos por segundo de vibración.
Para que un cuerpo o sistema pueda
vibrar debe poseer características potenciales y
cinéticas. Nótese que se habla de cuerpo y sistema si un
cuerpo no tiene la capacidad de vibrar se puede unir a otro y
formar un sistema que vibre; por ejemplo, una masa y resorte
donde la masa posee características energéticas
cinéticas, y el resorte, características
energéticas potenciales.
Otro ejemplo de un sistema vibratorio es una masa y una cuerda
empotrada de un extremo donde la masa nuevamente forma la parte
cinética y el cambio de
posición la parte potencial.
Definición 1.2 (b)
Vibración mecánica: es el movimiento de
vaiven de las moléculas de u cuerpo o sistema debido a que
posee características energéticas cinéticas
y potenciales.
En cualquiera que sea el caso, la excitación es el
suministro de energía. Como ejemplos de excitación
instantánea tenemos el golpeteo de una placa, el
rasgueó de las cuerdas de una guitarra el impulso y
deformación inicial de un sistema masa resorte, etc.
Como ejemplo de una excitación constante tenemos el
intenso caminar de una persona sobre un
puente peatonal, un rotor desbalanceado cuyo efecto es
vibración por desbalance, el motor de un
automóvil, un tramo de retenedores es una
excitación constante para el sistema vibratorio de un
automóvil, etc.
Vamos a ver varias formas de clasificar el estudio de las
vibraciones mecánicas.
Vibración libre: es cuando un sistema vibra
debido a una excitación instantánea.
Vibración forzada: es cuando un sistema vibra
debida a una excitación constante.
Esta importante clasificación nos dice que un sistema
vibra libre mente solo y solo si existe condiciones iniciales, ya
sea que suministremos la energía por medio de un pulso (
energía cinética) o debido a que posee
energía potencial, por ejemplo deformación inicial
de un resorte.
Esta energía es disipada por el fenómeno llamado
amortiguación, en ocasiones es despreciable.
Aun cuando la energía es disipada durante la
vibración, en le caso de la vibración forzada esta
descompensada por la excitación constante.
Vibración amortiguada: es cuando la
vibración de un sistema es disipada.
Vibración no amortiguada: es cuando la
disipación de energía se puede disipar para su
estudio.
El amortiguamiento es un sinónimo de la perdida de
energía de sistemas
vibratorios. Este hecho puede aparecer como parte del
comportamiento interno de un material, de rozamiento, o bien, un
elemento físico llamado amortiguador.
Vibración lineal: si los componentes básicos de
un sistema tienen un comportamiento lineal la vibración
resultante es lineal.
Vibración no lineal: se produce si alguno de sus
componentes se comporta como no lineal.
El comportamiento lineal de un elemento facilita su estudio,
en la realidad todo elemento de comporta como no lineal pero los
resultados de su estudio no difieren, en su mayoría, a los
realizados si se consideran como elementos lineales.
Un ejemplo de ello es el resorte, donde según la
ley de Hooke
el comportamiento fuerza-deformacion es lineal (fig 1.2)


Cuando el comportamiento vibratorio de un
sistema se puede representar por medio de una ecuación
matemática
entonces se dice que la vibración es deterministica, pero
si se tiene que determinar por ecuaciones
probabilísticas entonces la vibración es
probabilística o random. (fig 3.1)
Si el comportamiento determinístico se repite de
igual forma después de cierto tiempo entonces
la vibración es periódica, de la contrario es no
periódica.


Fig 3.1 Vibración deterministica
(a) y Random (b)
Si las características de señal de la
vibración de un sistema se asemeja a una señal
senoide, entonces se dice que la vibración es
senoide.
Una señal compleja a simple vista no se pude
representar por medio de una ecuación matemática, pero si puede ser determinado
por medio de senos y cosenos.


Fig. 1.4 toda señal compleja puede
ser representada por la suma de senos y cosenos (llamados
armónicas)
Este descubrimiento de Fourier adquiere importancia ya
que el análisis de los armónicos de una
señal nos puede revelar posibles fallas en una
maquinaria.
Fig 1.5


Frecuencia natural.- es la
frecuencia propia de un cuerpo o sistema al poseer elementos
elásticos e inerciales. Es la frecuencia resultante de la
vibración libre.
Resonancia.- es cuenco la excitación es de
frecuencia igual a la frecuencia natural
El efecto de resonancia en la guitarra se debe cuando
está afinada y al colocar el dedo en el quito trasto en la
sexta cuerda y se hace vibrar, la quinta cuerda vibra sola por el
efecto de resonancia, ya que el tono de la sexta cuerda en el
quinto trasto es de MI, la cual es la nota de la quinta
cuerda.
Fig 1.6

Definición 1.3.A
Grado de libertad.- es
el mínimo número de coordenadas requeridas e
independientes para determinar completamente la posición
de todas las partes de un sistema en un instante.



SISTEMAS DE 1 GRADO DE
LIBERTAD


fig. 1.7 Grados de libetad
Definición 1.3.B
Modelo matemático: es la representación de
todas las características importantes de un sistema con el
propósito de derivar las ecuaciones
matemáticas que determinen su
comportamiento.
El modelo
matemático debe incluir los mínimos detalles del
sistema tal que dicho comportamiento pueda ser representado por
una ecuación.
El modelo matemático puede ser lineal o no lineal.
Un modelo matemático permite soluciones
rápidas y simples, sin embargo los modelos no
lineales, revelan algunas veces ciertas características
del sistema que los modelos
lineales no proporcionan.
Algunas veces, durante el procedimiento del
análisis, el modelaje se realiza en forma gradual, esto
dependiendo de los componentes. (Fig. 14.7)



2
ELEMENTOS DE SISTEMAS VIBRATORIOS
Para que un sistema pueda vibrar debe poseer
elementos que puedan adquirir energía cinética y
elementos capaces de almacenar energía
cinética.
El análisis cinético es el
procedimiento que le sigue al modelaje matemático, es por
eso que el estudio de sistemas dinámicos se vuelve
esencial para el estudio de las vibraciones
mecánicas.
Un sistema vibra si posee energía
cinética y potencial, la carencia de uno de ellos anula la
posibilidad, es por eso que en esta unidad se hace un estudio a
los sistemas dinámicos desde el punto de vista de la 2da
ley de Newton y de la
conservación de la masa.
También se hace un estudio a la ley de Hooke y
del calculo de la constante elástica equivalente de
sistemas que posean diferentes elementos
elásticos.
Son tres los elementos básicos de un sistema
vibratorio: la masa, elementos elásticos y elementos
absorbedores de energía.
Vamos a analizar estos tres elementos desde el punto
de vista cinético, tanto por medio de la ecuación
de la segunda ley de Newton como de
la conservación de la energía.
2.1 MASAS
2.1.1 La segunda ley de Newton.
La primera y la tercera ley de Newton se utilizan para
analizar sistemas elásticos, para sistemas
dinámicos la segunda ley de Newton resulta
apta.
Un cuerpo de masa "m" puede poseer diferentes tipos de
movimiento de los cuales tenemos:
Movimiento rectilíneo: un cuerpo de masa "m"
sometido a un sistema de fuerzas S F poseerá una aceleración
rectilínea x T.Q. (Fig. 2.1)


Movimiento Rotacional Centroidal: Un cuerpo
con un movimiento de inercia de masa con respecto a su centro
de gravedad ‘JG’ y aceleración angular
θ queda determinado como (fig. 2.2)


=
Movimiento Rotacional Excentroidal: un cuerpo con este
tipo de movimiento (fig 2.2) es idéntico al centroidal,
porque el análisis es el pivote


=
Movimiento Combinado: cuando un cuerpo posee
movimiento rectilíneo y angular se dice que su
movimiento es combinado, en ocasiones el análisis se
puede sustituir por uno solo. ( ver ejemplo 2.2)
Ejemplo 2.1
Una varilla de masa ‘m’ y longitud
‘l’ se suelta del reposo. Determine las ecuaciones
del
movimiento, si el sistema ha girado un ángulo
θ a partir del eje vertical.


Ejemplo 2.2
Determine la ecuación del movimiento angular del
sistema mostrado en la Fig.,

Solucion:
Como la esfera tiene los dos tipos de movimientos se
puede analizar por separado o como un sistema
único.
1.- Análisis individual.

2.- Análisis único.
Como tenemos rodadura para el punto ‘p’ es
el centro instantáneo de velocidad
cero, por lo tanto haciendo momentos en
‘p’

2.1.2 Energía
un cuerpo de masa ‘m’ con movimiento puede
poseer energía potencial y/o cinética.
Energía cinética de
traslación: un cuerpo de masa ‘m’ con
movimiento de traslación a velocidad
‘x’ posee una energía cinética
igual:
ECT=1/2 mx2
Ec. 2.4
Energía cinética de
rotación: un cuerpo de masa
‘m’ y un momento de inercia de masa c respecto al
pivote ‘p’ Jp y una velocidad angular
“θ”
ECR=1/2 Jp
θ2 Ec.
2.5
Energía potencial gravitacional: un cuerpo
de masa ‘m’ que esta a una altura ‘h’ de
una referencia poseerá una energía potencial
igual.
EPG= mgh Ec.
2.6
El análisis de
sistemas con movimiento combinado se facilita con el método de
energías.
Ejemplo 2.3
Calcule la energía cinética total del
sistema mostrado en la Fig.

- Se puede analizar de 2 maneras: a) sumando ambas
energías. b) como una energía
única.
1.- Como sistema separado:
Ec Total= ECR + ECT = 1/2
JG θ2
+ 1/2 mx2
Como x = θr
Ec Total= = 1/2 JG
θ2 + 1/2
mx2 = ½ (JG + mr2
) θ2
2.- Como sistema único.
Como tenemos rodadura pura en ‘p’ este es su
centro instantáneo velocidad cero,
por lo tanto:
Ec Total: ECP = ½ JP
θ2
Como: JP = JG +
mr2
Ec Total: ( ½ JG +
mr2 )
θ2
2.2 ELEMENTOS ELASTICOS
2.2.1 Resortes y la Ley de Hooke
Los resortes son uno de los elementos elásticos
utilizados en sistemas vibratorios, estos pueden ser lineales o
no lineales.
Si la causa-efecto se conserva, entonces el resorte es
lineal, o bien se dice que es perfectamente elástico, cosa
que se puede suponer en muchos problemas de
la técnica (Fig. 2.4).

Aun cuando se tenga un resorte no lineal, este se puede
utilizar sobre un punto de operación tal que sobre ese
punto ‘p’ el resorte es lineal (Fig. 2.4)
Un ejemplo de un elemento no lineal es el caucho, cuyo
material es usado con frecuencia y donde la relación F
– X tiene una variación no lineal.

El estudio de resortes o elementos no lineales no
corresponde a este capitulo, mas sin embargo vamos a ver unos
ejemplos.
El primer ejemplo de un sistema mecanico es el mostrado
en la figura 2.5, donde la contante elastica equivalente
‘Keq’ no es contante
La linealidad se rompe al entrar en accion el resorte K3
o K4.
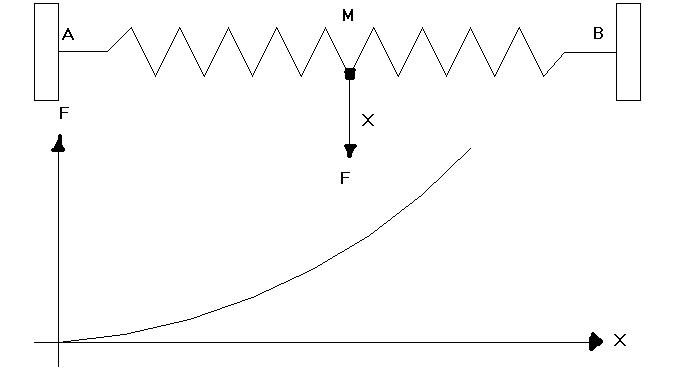
Otro caso muy ilustrativo es el de un Resorte
estirado entre dos puntos fijos A y B y en donde la masa
‘m’ esta atada a un punto del resorte.
Si se aparta m lateralmente y se deja Oscilar, se
encuentra que F(x) no es lineal. (Fig. 2.6).

Otro caso interesante y que posteriormente va a
ser muy estudiado es el de un péndulo (Fig.
2.7)
Si se consideran oscilaciones pequeñas la
ecuación diferencial que determina el movimiento
es:
L θ + θ = 0 è Ec, Dif. Lineal.
Si consideramos el caso del resorte ineal, la ley de
Hooke nos dice que la fuerza
aplicada es directamente proporcional a la deformación,
osea:
F a x
Donde F= fuerza x= deformación, para eliminar la
proporcionalidad agregamos una constante proporcional agregamos
una constante K
F= -K x
En términos funcionales la
ecuación correcta es:
F(x)= K x
La ecuación gráfica de la
Ley de Hooke a saber es una pendiente (fig. 2.8) donde la
constante es el valor de la
pendiente.

Definición 2.2.A.-
Resortes en serie : 2 o más resortes están
en serie si la fuerza se transmite en la misma proporción
en cada uno de ellos.

2.2.2 ENERGÍA
cuando se estira o se comprime un resorte elástico
una distancia x de su posición no deformada, la
energía potencial Epr elástica de puede
expresar:
Epr= ½ K x2

en este caso la fig 2.12 la
energía es siempre positiva ya que en lo posición
deformada la fuerza del resorte tiene la capacidad de hacer
trabajo al regresar a su posición no deformada.
2.3 ELEMENTOS ABSORVEDORES DE
ENERGÍA
La ley de conservación de la energía
establece que la energía no se crea ni se destruye
sólo se transforma.
La fricción es un ejemplo de pérdida de
energía.
El amortiguamiento es un sinónimo de
absorción de energía en los sistemas
vibratorios.

1-. Sistemas:
se puede observar que el desplazamiento transversal de
la viga en cantiliver K2 es igual a la del resorte K1 por lo
tanto estan en paralelo.

2.- sistema :
Aquí el desplazamiento en cada uno de ellos es
diferente, tal vez es mas facil ver por la fuerza transmitida ya
que se transmite en la misma proporcion por lo tanto estan en
serie.

3.- sistema:

Aquí tenemos una combinación el elemento
K1 y K2 estan en paralelo y todo el conjunto esta en serie con
K3.
Por lo tanto en el caso en que los resortes esten
en paralelo tenemos:
Xt = X1 = X2
Sin embargo la fuerza se distribuye, en cada uno
de:
Fr = F1 + F2
Nuevamente, como:
FT = KT XT
F1 = K1 X1
F2 = K2 X2
Sustituyendolo en la ecuación 2.10
tenemos
KT XT = K1X1 + K2X2
Pero como XT = X1 = X2
KT = K1 + K2
En resumen tenemos:
Definición 2.2.B
Si dos o mas resortes estan conectados en paralelo el se
puede sustituir por uno equivalente de la forma:
Keq = K1+ K2 + K3 + ….. Kn
Es facil identificar si 2 o mas resortes estan pero
cuando se tienen otros elementos, por ejemplo, se torna un poco
mas difícil identificarla.
Dependiendo del empotramiento y de las dimensiones, peso
de las vigas será su constante elástica.
Por otro lado el desplazamiento total es igual a la suma
de cada uno de ellos, de tal forma que:
XT = X1 + X2

Vamos a ver como podemos representar 2 o mas resortes en
serie por uno equivalente
Ft = Xt Kt Xt = Ft/Kt
F1 = X1 K1 X1 = F1/K1
F2 = X2 K2 X2 = F2/K2
Sustituyendolo en la Ec 2.9
Ft = F1 + F2
Kt K1 K2
Como Ft = F1 = F2 tenemos que:
1 = 1 = 1
Kt K1 K2
Llamando Keq a los Kt resumimos:
Definición 2.2.D
Dos o mas resortes conectados en serie, la constante
elastica equivalente al efecto de todas queda determinada
como
1 = 1 + 1 + ……..
1
Keq K1 K2 Kn
Vamos a analizar el caso en Que se tenga 2 o mas
resortes
En paralelo. (Fig. 2.11)
Definición 2.2.C
Resortes paralelo: 2 o mas resortes Estan conectados en
paralelo si el Desplazamiento en cada uno de ellos Es el
mismo.

Con viscosidad, la
fuerza es directamente proporcional, mientras que en la
turbulenta la fuerza es proporcional al cuadrado de velocidad. En
la amortiguación sera (o de Coulomb) la fuerza es
constante, el amortiguamiento solido es debido a las fuerzas
internas.
- Amortiguamiento viscoso F a x
- Amortiguamiento turbulento F a x2
- Amortiguamiento seco F = cte
- Amortiguamiento solido
Uno de los amortiguadores mas presentes en sistemas
vibratorios es el viscoso. En los resortes existe la contante
elastica K que elimina la proporcionalidad de F
a X. En los
amortiguadores del tipo viscoso existe otra copntante
l¿lamada coeficente de amortiguamiento y generalmente se
denota como ‘C’.
De tal forma que la fuerza de un amortiguador
‘Fd’ queda determinada como :
Fd = -cx (Ec. 2.12)
Donde las unidades para el sistema M.K.S son:
Fd = New x = m/s c = Nw – s
Mt
Ejemplo 2.5
El amortiguados mostrado en la figura tiene una fuerza
de 98 New a una velocidad de 0.01 m/s2 Calcule el
coeficiente de amortiguamiento.

Fd = cx
C = Fd = 98
X 0.01
C = 9800 Nw – s
Mt
Aunque los sistemas vibratorios generalmente trabajan
como sistemas forzados el análisis de
sistemas libres adquiere importancia debido a que uno de los
problemas a
los que "las maquinas temen" es la resonancia.
Según la definición 1.2 H la
resonancia se presenta cuando la frecuancia de excitación
es igual a la frecuencia de resonancia.
Según la definición 1.2 G la
frecuencia natural es la frecuencia de los sistemas vibratorios
en la vibración libre, de aquí que el calculo de
frecuencias naturales es importante.
En este capitulo se expondran diferentes metodos
para el calculo de fracuencia natural, sus ventajas y demas,
apartir de un modelo tipico.
Consideremos el caso general en que el existe un
amortiguamiento, y luego se analizara para diferentes valores de
amortiguamiento incluyendo el despreciable.
3.1 Movimiento armonico
el movomiento armonico es importante de estudiar ya que
tiene similitud con muchos movimientos de sistemas vibratorios,
todo movimiento periodico debe satisfacer:
x (t) = X (t + t ) Ec 3.1
Vamos a ver que significa esto. Un movimiento periodico
es un movimiento que se repite a intervalos de tiempo llamados
periodos ‘t
’.
La frecuencia se define como el numero de ciclos por
unidad de tiempo, de tal forma que se relaciona con el periodo
dela forma
F = 1 (Ec. 3.2)
t
Las unidades de la ecuación 3.2 son ciclos/seg
ó Hertz
La figura 3.1 muestra un
ejemplo de un movimiento periodico en donde la grafica de la
posición de una particula ‘P’ en funcion del
angulo se muestra.

Fig. 3.1 Movimiento Armonico
En la fig. 3.1 se puede observar el máximo
valor llamado
la amplitud ‘A’.
Ahora si no se conociera el centroide existe una forma
sencilla de calcularlo y es aprovechando el equilibrio
estatico ya que cuando el cuerpo esta estatico el centro de
gravedad esta por una linea imaginaria vertical al
pivote.

3.2 vibración libre no
amortiguada.
En este apartado se estudiara el modelo mas simpole de
tal modo que una ecuación matemática denotara su
comportamiento.
Este modelo lo llamaremos el modelo tipico, y la
ecuación diferencial que determina su comportamiento lo
llamaremos la forma canonica de un sistema libre no
amortiguado.
La fig. 3.2 muestra este modelo un sistema de masa
‘m’ y una constante elastica ‘k’ vamos a
realizar un estudio estatico y cinético con el fin de
determinar la ecuación diferencial que determinara el
movimiento posteriormente veremos la solucion de la
ecuación diferencial para ver la respuesta en el tiempo
del sistema asi como la formula que determina el calculo de la
frecuencia natural.

Fig. 3.2 modelo tipico de un sistema
libre no amortiguado.
Supongamos tres casos como se muestra en la figura
3.3.

En la figura 3.3 (a) se tiene el resorte sin
deformar, posteriormente se coloca una masa ‘m’ y el
resorte sufre una deformación Xs que llamaremos
deformación eststica; de aquí
Fk = KXs

Fig 3.4 diagrama de
cuerpo libre, análisis estatico.
El diagrama de
cuerpo libre estatico nos rebela que
S Fy = 0
mg – KXs = 0
mg = Kxs Ec.3.3
ahora imagfinemos que estiramos la masa una distancia X
y luego lo soltamos y aquí comenzamos hacer el
análisis.

La figura 3.5 nos muestra el diagrama de cuerpo
libre como consideramos X + 1 por lo tanto x y x seran positivos
hacia abajo.
Utilizando la 2da ley de Newton
+ S fy
= S fy
efect = mx
mg – KXt = mx Ec. 3.4
Como KT = Xs + x la ecuación 3.4 se convierte
en:
Mg – KXs – Kx = mx Ec 3.5
Utilizando la ecuación 3.3 como en la
ecuación 3.5 aparecen como constantes se pueden eliminar,
por lo tanto:
Mx + kx = 0 Ec. 3.6
A la ecuación 3.6 se le conoce como la
ecuacion diferencial del movimiento de un sistema libre no
amortiguado. Si existe deformación estatica el efecto
que produce la masa se coloca con un resorte cuando se deforma
estaticamentepor lo tanto vamos a buscar la solucion utilizando
la transformada de laplace.
Si analizamos el termino angular ( √K (t) )
cuya unidad debera ser los radiantes, por lo tanto:
√m
√K T = seg
√m
de aquí que el termino √K es la
frecuencia natural en otras unidades
√m
por lo tanto la ec 3.7 que denota la la respuesta en el
tiempo del sistema queda:
determinado su movimiento por la ecuación
diferencial:
mx + kx = 0
cuya solucion, queda determinada la respuesta en el
tiempo:
x(t) = x(0) cos wnt + x(0) sen wt
wn
donde: x(0) = deformación inicial
x(0) = velocidad inicial
wn frecuencia natural (rad/seg)
la frecuencia natural queda definida como:
Wn = √K
√m
analizando la ec. 3.11 vamos a analizar su grafica
respuesta en el tiempo.
Caso 1 si el sistema parte con velocidad 0; es decir
x(0)

Caso 2: si el sistema parte con velocidad inicial
x(0) y sin deformación, es decir x(0)

Puede ser un problema, mas sin embargo solo hay que
dedicarse a llegar a la ecuación diferencial y esta se
asemeja a la ecuación 3.6
Definición 3.2.B
Forma canonica de un sistema libre no
amortiguado
A + B = 0
Donde
= d2 / dt
2.3 METODOS PARA EL
CALCULO DE ECUACIONES
DIFERENCIALES DE SISTEMAS LIBRTES NO
AMORTIGUADOS
Algunos sistemas vibratorios pueden ser expresados a la
forma canonica (def 3.2.B) y posteriormente calcular su
frecuencia natural y/o respuesta en el tiempo.
Existen tres metodos básicos para el calculo para
el calculo de ecuaciones
diferenciales de sistemas vibratorios libres no amortiguados,
cada uno de ellos presenta ventajas dependiendo del
movimiento.
Movimiento rectilíneoè 1° metodo de
Newton F = ma
Movimiento angularè 2° metodo de Newton
(momentos)
Movimiento rect y/o angular è metodo de energia.
Por lo tanto el primer tip´es identificar el tipo
de movimiento para ver el metodo apropiado para calcular la
ecuación diferencial.
Si el sistema posee movimiento rectilíneo
utilizar el analisis cinetico S fy = S fy efect = mx es apropiado sollo
hay que llegar a la ecuación diferencial del
movimiento.
Ejemplo3.1
Un resorte de constante elástica ‘K’
es empotrado de un extremo mientras que el otro extremo se coloca
una masa de 4.53 kg logrando tener un periodo natural de 0.45
seg. Posteriormente el resorte se parte justo a la mitad
empotrándose de los extremos y colocando la masa en el
punto medio. Calcule el periodo natural nuevo.

Solucion:
Aquí no es necesario hacer un analisis Cinetico
ya que la ecuación Diferencial es directa.
0.453 x + kx
vamos a analizar los sistemas por separado analizando el
sistema (a)
Wn = √K =
√K è K=Wn12 m =
(13.95)2 (4.53)
√m 0.453 k=887.54 Nw/m
Analizando el sistema (b)
Para ver como afecta la constante al dividirse a la
mitad partimos de la formula para calcular la constante en
función
de sus características
K= Gd4 n = # vueltas k’ =
Gd4 = 2K K’= 2K
64R3n 64R3(n/2)
como están en paralelo
Keq= K’ + K’ = 2K +2K = 4K Keq = 4 (
882.25) = 3526 Nw/mt
Wn = √Keq = √3526 = 88.22
rad/seg
√m √0.453
un elemento elástico de constante desconocida
sufre una deformación estática
‘Xs’ al colocarle una masa ‘m’. calcule
la frecuencia natural.
Solución:
La constante elástica k se puede calcular a
partir de la ley de Hooke mg= KXs k=mg/xs sustituyéndolo
en la formula de la frecuencia natural.
Wn = √K = √mg = √g Wn =
√g
√m √mxs √xs
√xs
- 2° METODO DE NEWTON (MOMENTOS):
S M=Jp
θ Si el sistema vibratorio tiene movimiento angular
utilizar la segunda ley de Newton nos ayudara a encontrar
su ecuación diferencial.En terminos generales:
S
Mp = S
Mpefect = Jp θ +
S miairi Ec
3.12Para un movimiento rotacional donde el unico
momento inercial es el rotacional.S Mp = Jp θ Ec.
3.13Como ‘tip’ para el signo del momento
podemos considerar el sentido del angulo de
excitación (fig 3.7)Péndulo simple o
compuesto.Calcule la frecuencia natural del péndulo
simple y compuesta
Análisis del péndulo simple
(oscilaciones pequeñas senθ =
θ)
S Mp =
S
Mpefect = Jp
θ-mg senθl =Jpθ
Jp=JCG + ml2 (teorema de
ejes paralelos)JCG = 0 (masa Puntual)
Sen θ ~ θ (θ <=15°)
(linealidad)-mg senθl =Jpθ è mglθ =
ml2θml2θ + mglθ =
0lθ + gθ = 0 è ec
diferencialWn = √g
√l
Análisis del péndulo compuesto
(oscilaciones pequeñas sen θ ≠
θ)S Mp =
S
Mpefect = Jp
θ-mg senθl =Jpθ sen θ =
θJp θ + mgθ = 0 ec
diferencialWn = √mg
√Jp Jp = Jcg + mr2

En el apartado 3.2 se estudio el modelo tipico, en
el estudio dinamico se llego a la ecuación 3.5 pero
debido a la ecuación 3.3 en la nota de esa ,isma
paguina (parte superior) se llego a la conclusión de
que: " el efecto que produce la masa es compensado por el
efecto del resorte en la deformación estatica si el
resorte es deformado inicialmente".Si el sistema posee varias masas y los elementos
elásticos estan deformados las masas que que
producen esa deformación no produce
efecto.Ejemplo:
El efecto de orientación
Una masa puntual ‘m’ se empotra a uina
varilla delgada de masa despreciable y una longitud’
‘l’, se coloca un resorte de constante
‘K’ a una distancia ‘R’ del pivote
‘p’. Calcule la frecuencia natural Wn para cada
una de las siguientes configuraciones.


Solucion caso (a)

S Mp = Jp
θ-t
2 – t 1 = Jp
θt
1 = Kxr =) k (rsen θ) r
= k2 sen θ =
r2 θ– k2 sen θ = mg sen
θl = mglθ
Al colocar la masa ‘m’ o quitarla, el
resorte se deforma o restaura respectivamente, esto indica
que el efecto se compensa, es decir, el momento generado
por ‘m’ es compensado por el resorte en la
deformación inicial y no se coloca en la
ecuación.
S
Mp = Jp θt 2 – t 1
= Jp θt
1 = kxr = K (rsenθ)r =
Kr2θt
2 = mg sen θ l =
mglθJp = JcG + mr2
Mr2θ +
Kr2θ –
mglθ
mr2θ+(Kr2
– mgl) θ = 0Wn = √Kr2 –
mgl√mr2 Condición de
movimientoKr2 > mgl
- METODO DE ENERGIA
Si el sistema posee movimiento de rotación y/o
traslación este método es efectivo. Este
método se basa en el principio de la conservación
de la energía y que dice:
Ec1 + Ep1 = Ec2 +
Ep2
Ec = Energía Cinética
Ep = Energía potencial
Σp ( EC + Ep
) = cte| tiempo Ec. 3.14
Derivando la ec. 3.14 con respecto al tiempo
d/dt Σp (Ec +
Ep) = 0 Ec 3.15
La ecuación 3.15 nos conducira a la
ecuación diferencial, cabe señalar que este metodo
es apropiado si y solo si no hay disipación de energia, es
decir, no existe amortiguamiento.

Ejemplo 3.5
Aquí podemos observar que existe
tanto la energia cinética rotacional como de
traslación, tambien existe energia potencial elastica y
energia potencial gravitacional. Aunque si observamos al colocar
o quitar el contrapeso ‘m’ el resorte se alarga o
restaura respectivamente, por lo que su efecto es compensado y no
aparece como energia potencial gravitacional.
Σp Ec + E =
cte|tiempo
Ecr + Ect + Epr = cte
1/2 Jp θ2 +
1/2m2+ ½ Kx2
½ (1/2 Mr2)
θ2 + ½
mr2 + ½ r2θ =
cte
d/dt [ ½ (1/2 Mr2)
θ2 + ½
mr2 + ½ r2θ = cte
] d/dt θ = θ
1/2 Mr2 θ +
mr2θθ +
Kr2θθ = 0
d/dt θ = θ
1/2 Mr2 θ +
Kr2 + mr2
) θ = 0 ec diferencial.
Wn = √Kr2 –
mr2
√1/2mr2
- UN CASO ESPECIAL
Si el sistema tiene movimiento angular conviene el
2° método de Newton y si su movimiento es
angular y rectilíneo conviene el de
energias.Estas sugerencias no siempre del todo validas
dependen del sistema e incluso del punto de
análisis, como por ejemplo consideremos el siguiente
sistema:

Metodo de Energias
 + Σ Ma = Ja θ
+ Σ Ma = Ja θ-Kx (2r) = Ja θ
x’ = 2x = 2(rθ)
-4 Kr2θ =
Jaθ Jaθ + 4
Kr2θ = 0 Ec
3.19¿Cual resulto mas
sencillo?- CALCULO DE
MOMENTO DE INERCIA Y CENTROIDES.
Si se tuviera un
cuerpo de geometría
extraño de tal forma que su centroide y momento de inercia
no se puede calcular analíticamente haciendo oscilar el
cuerpo y tomando muestras de periodos.
Considerando el cuerpo como un péndulo compuesto
tenemos:

Si se conoce el centroide entonces se conoce r
que es la distancia del pivote al centro de gravedad, de la
formula del péndulo compuesto.
Wn = √ mgr2
(Rad/seg)
√Jp
fn = π √
mgr2 (Ciclos / seg)
2 π √Jp
THE DOGGFATHER












 + Σ Ma = Ja θ
+ Σ Ma = Ja θ