El presente trabajo
corresponde al Capítulo II del libro de mi
autoría: GUIA RAPIDA " Y MATEMATICAS DE LA MERCADOTECNIA"
Serie MYPES. Esta obra –como todas mis producciones-
estará difundiéndose gratuitamente en Internet en archivos Word y en
impresión digital PDF.
- 1.
Introducción - 2. Los
Estados Financieros en la Empresa - 3. Ratios
o razones analíticas - 4.
Márgenes de Utilidad y Rebajas - 5.
Las matemáticas en la investigación de mercados y
muestreo - 5.1.
Alcances de la investigación de
mercado - 5.2.
Excel y las Funciones Estadísticas para muestras y
poblaciones - 5.2.1. Algunos
conceptos importantes
5.2.2. Notación con índice o
subíndice- 5.2.3.
Notación sumatoria - 5.2.4.
Herramientas de análisis
estadístico - 5.2.4.1.
Medidas de posición central - a) Media o
promedio - Función
PROMEDIO - b)
Mediana - Función
MEDIANA - c) Moda
- Función
MODA - 5.2.4.2.
La desviación típica y otras medidas de
dispersión - Cuartiles,
Deciles y Percentiles - d)
Desviación media absoluta, o promedio de
desviación
e) Desviación típica o desviación
estándar- f)
Varianza - 5.2.4.3.
Cálculos estadísticos con Excel, con el total de
la población - Función
VARP - Función
DESVESTP - 5.2.4.4.
Cálculos estadísticos en Excel con la
muestra - Función
DESVEST - Función
VAR - 5.3.
Poblaciones y muestras - 5.3.1.
Tamaño de la muestra - 6. El Punto
de Equilibrio (Pe) - 6.1. Punto
de equilibrio en dinero y en unidades - Relación
de aportación - 6.2.
Punto de equilibrio para varios productos o
servicios - 6.3.
Eliminación de productos o servicios - Bibliografía
La mayoría de textos de mercadotecnia omiten
las matemáticas de la mercadotecnia, no
obstante ser tan importantes en muchas decisiones para este
campo. El cálculo
de las ventas,
costos y
ciertas razones permiten al estratega de mercadotecnia tomar
medidas acertadas. En este libro describimos cinco
áreas principales de la matemática de la mercadotecnia: el
estado de
resultados, las razones analíticas, los
márgenes de utilidad y
rebaja, las matemáticas en la investigación de mercados, muestreo y el
punto de
equilibrio.
2.
Los Estados
Financieros en la Empresa
Como vimos en el capítulo I, los principales
estados financieros que utilizan las empresas son
dos: el estado de
resultados y el balance
general.
El balance general muestra los
activos, los
pasivos y el patrimonio
de una empresa en
determinado momento. Mide la riqueza de la
empresa.
El estado de
resultados (llamado también estado de
pérdidas y ganancias o estado de ingresos) es el
principal de los dos estados para obtener información de mercadotecnia. Muestra las
ventas de la empresa, el
costo de los
bienes
vendidos y los gastos durante
el período dado de tiempo.
Refleja la actividad económica de una empresa en
determinado momento. Al confrontar el estado de resultados de
un periodo a otro, la firma puede detectar tendencias positivas
o negativas y emprender las acciones
más pertinentes.
EJERCICIO 01 (Analizando el Estado de
Resultados)
Debemos establecer la utilidad neta de la empresa AZY,
con ventas netas anuales de UM 430,000, siendo sus costos de
mercadería vendida la suma de UM 254,400 y sus gastos
totales de UM 145,846.

El cuadro 1-1, presenta el estado de pérdidas y
ganancias de la compañía AZY (tienda de muebles
para oficina), al 31
de diciembre del 2004. Corresponde al estado de una tienda
minorista. El de un fabricante sería diferente;
concretamente, el área de compras en
«costo de bienes vendidos» los reemplazaría
por «costo de bienes fabricados».
Aplicando el esquema general de pérdidas y
ganancias tenemos:
Ventas netas UM 430,000
(-) Costo de bienes
vendidos 254,400
Margen Bruto 175,600
(-) Gastos 145,846
Utilidad neta 29,754
El primer elemento del estado de resultados, nos
detalla lo que la compañía AZY vendió
durante el año. Las cifras de ventas están
formadas por tres conceptos: ventas brutas, devoluciones y
descuentos, ventas netas. El primero representa el importe
total que se carga a los clientes
durante el año por mercadería adquirida en la
tienda AZY. Es usual que algunos clientes devuelven
mercadería por defectos o por que cambian de parecer. El
reintegro íntegro de dinero o el
crédito completo al cliente es
denominado «devolución». Quizás
decida conservar la mercancía, si la tienda le rebaja el
precio para
compensar el defecto. Estos son las «bonificaciones por
defecto». Los ingresos al término de un año
de ventas (ventas netas) lo obtenemos deduciendo las
devoluciones y rebajas de las ventas brutas.
Ahora examinaremos el costo de los bienes que AZY
vendió en el 2003.
Desde luego, para el análisis incluiremos el inventario
inicial del negocio. Durante el año compraron
artículos diversos para la venta
(escritorios, sillas fijas, giratorias, credenzas, gavetas,
etc.) por valor de UM
244,800.
El proveedor concedió un descuento de UM 24,000
a la tienda; por tanto, las compras netas fueron de UM 220,800.
Como la tienda está situada en una población pequeña, necesita una
ruta especial de entrega, AZY tuvo que pagar UM 14,400 por
concepto de
flete, lo que le da un costo neto de UM 235,200. Cuando sumamos
al inventario inicial este monto, el costo de los bienes
disponibles para su venta asciende a UM 321,600. El inventario
final de UM 67,200 en muebles que había en la tienda al
31 de diciembre lo restamos y obtenemos UM 254,400 que viene a
ser el «costo de los bienes vendidos». Como vemos
en este caso seguimos una serie lógica de pasos para llegar al costo de
los bienes vendidos:


El margen bruto (UM 175,600) es la diferencia entre lo
que AZY pagó (UM 254,400) y lo que recibió (UM
430,000) por su mercancía (430,000 – 175,600 = UM
175,600).
Para determinar lo que AZY «ganó»
al final del ejercicio, restamos al margen bruto los
«gastos» efectuados para generar ese volumen de
ventas. Los gastos de venta incluyen el sueldo de dos empleados
de tiempo parcial; publicidad
local en prensa,
radio,
televisión; y el costo de entrega de
mercancía a los consumidores. Los gastos de ventas
equivalían a UM 72,000 para el año. Los gastos
administrativos incluyen el salario de
un contador a tiempo parcial, suministros de oficina como
papelería, tarjetas de
negocio y diversos gastos de una auditoría
administrativa llevada a cabo por un asesor externo. Los
gastos administrativos fueron de UM 44,308 en el 2004.
Finalmente, los gastos generales de renta, servicios
públicos seguros y
depreciación fueron en total de UM
29,538. Los gastos totales fueron de UM 145,846 para el
año. Al restar los gastos totales de UM 145,846 del
margen bruto (UM 175,600), llegamos a las utilidades netas de
UM 29,754 para AZY durante el año del 2004.
3. Ratios o
razones analíticas
El analista del estado de pérdidas y ganancias
nos proporciona los datos
necesarios para derivar varios ratios claves.
Específicamente, estos índices son los ratios de
operación (es decir, la razón de determinados
conceptos en el estado de operación con las ventas
netas), que permiten a las empresas comparar su rendimiento en
un año, con el de años anteriores (o con los
estándares o competidores de la industria en
el mismo año); con el propósito de evaluar el
éxito
global de la compañía. Los principales ratios de
operación que se calculan son: los porcentajes de margen
bruto, utilidades netas, gastos de operación,
devoluciones y rebajas. Los ratios presentados en el presente
capítulo, son complementarios del capítulo
anterior.

Otro ratio importante para propósitos
analíticos es la tasa de rotación de inventarios
(RI). Esta tasa indica el número de veces que un
inventario se mueve o vende durante un periodo
específico (generalmente un año). Podemos
calcularlo a partir de un costo, venta o precio unitario.
Veamos las siguientes fórmulas:
Índices de Rotación de Inventarios
(RI):
![]() o bien:
o bien:
![]()
o bien:
![]()
Aplicando la fórmula (31) a nuestro caso,
tenemos:

Como vemos, el inventario de AZY rotó
más de 3.31 veces en el 2003. A una tasa mayor de
rotación de inventarios, corresponde una mayor eficiencia en
la
administración y utilidades mayores para la
empresa.
El rendimiento sobre la inversión (RSI)
mide la eficiencia general, opera con datos del estado de
resultados y del balance general.
![]()
Después de analizar la fórmula anterior
surgen como es natural, dos preguntas: ¿Por qué
usar un proceso de
dos etapas cuando el rendimiento sobre la inversión podría obtenerse
sencillamente como utilidad neta sobre la inversión?
¿Qué es exactamente la
inversión?
La respuesta a la primera pregunta, la obtenemos
observando como puede afectar cada componente de la
fórmula al RSI. Imaginemos que AZY calculó
el índice aplicando la fórmula (34):
![]()
Si AZY hubiera proyectado conseguir ciertas ventajas
de mercadotecnia aumentando su participación en el
mercado de
muebles, posiblemente habría generado el mismo
RSI, duplicando las ventas y permaneciendo sin
variación la inversión (aceptando una
razón de utilidad más baja, pero produciendo
operaciones
comerciales y repartición de mercado más
altas):
![]()
También es posible aumentar el RSI, con una
mayor utilidad neta mediante una eficaz y eficiente planeación, realización y control de
mercadotecnia:
![]()
Otra forma para incrementar el RSI, es encontrar el
modo de producir el mismo volumen de ventas y utilidades,
disminuyendo al mismo tiempo la inversión (quizá
reduciendo el tamaño del inventario promedio del
negocio):
![]()
¿Qué es la
«inversión» en la fórmula RSI? por
inversión entendemos el total de activos de una empresa.
Como vimos en el Capítulo I, existen otras medidas del
rendimiento para evaluar la eficiencia gerencial. Como la
inversión se mide en un punto del tiempo, es costumbre
calcular el RSI tomando la inversión promedio
entre dos periodos (por ejemplo, entre el 1° de enero y el
31 de diciembre del mismo año). También puede
medirse como una «tasa interna de rendimiento»,
empleando el análisis de flujo por pronto pago. La
importancia de emplear cualquiera de estos ratios es precisar
la eficacia con
que la empresa ha utilizado sus recursos. A
medida que la inflación, las presiones de la competencia y
el costo del capital
muestran un movimiento
ascendente, estos ratios adquieren más importancia como
parámetros de la eficiencia de la administración de mercadotecnia y de la
gerencia.
4.
Márgenes de Utilidad y Rebajas
Tanto para minoristas y mayoristas es imprescindible
conocer los conceptos de margen de utilidad y rebaja. La
empresa necesita obtener ganancias si quiere seguir en el
negocio; de ahí que el porcentaje de margen de utilidad
sea una consideración estratégica de capital
importancia. Tanto el margen de utilidad como la rebaja lo
expresemos en porcentajes.
A continuación describimos dos métodos
de calcular los márgenes de utilidad (con base en el
costo o en el precio de venta):
Porcentaje del margen de utilidad basado en el costo,
% MUC.
Porcentaje del margen de utilidad basado en el precio
de venta, % MUPV.
![]()
![]()
Para evitar confusiones AZY debe decidir cuál
fórmula utilizar. Por ejemplo si compró las
sillas a UM 40 y quiere obtener un margen de utilidad de UM 20,
este porcentaje de sobrecargo en el costo
será:
Margen de utilidad en UM : 20
Costo : 40
Sustituyendo estos valores en
la fórmula (29) tenemos:
![]()
Aplicando la fórmula (30) tenemos:
![]()
Es común en los minoristas calcular el
porcentaje de sobrecargo basándose en el precio de venta
y no en el costo.
Supongamos que AZY conoce su costo (UM 40) y el margen
de utilidad deseado (25%) en un sillón y quiere obtener
el precio de venta utilizando el margen de utilidad como
porcentaje de la fórmula para el precio de venta. La
fórmula es:

En el proceso de distribución de un producto,
cada integrante del canal añade su margen de utilidad al
producto antes de venderlo al siguiente integrante. Esta
«cadena de márgenes de utilidad» lo
ilustramos en el siguiente ejemplo con la venta de un juego de
muebles de AZY a UM 600:

El minorista cuyo margen de utilidad es de 25% no
necesariamente obtiene una utilidad mayor que el fabricante,
cuya ganancia es de 10%. La utilidad se condiciona al volumen
de venta, a la cantidad de artículos que pueden venderse
con ese margen de utilidad (tasa de rotación de
inventarios) y a la eficiencia de operación (gastos,
etc.). Generalmente al minorista le agrada convertir en costo
(y viceversa) los márgenes de utilidad basados en el
precio de venta. Ver fórmulas:
![]()
![]()
AZY, descubre que su competidor utiliza el 35% como
margen de utilidad, basado en el costo y desea saber
¿cuánto sería el porcentaje del precio de
venta? El cálculo arrojaría:
Sustituyendo valores en la fórmula (31)
obtenemos:
![]()
Como AZY estaba operando con 25% de margen de utilidad
basado en el precio de venta piensa que este recargo
será compatible con el de su competidor. Al finalizar la
campaña, AZY se dio cuenta que tenía en
existencia un inventario de sillones devueltos. Por lo que
resulta indispensable una rebaja del precio inicial de venta.
Compraron 40 unidades a UM 35 cada una y vendieron 20 a UM 70
la unidad. El saldo de sillones lo rebajaron a UM 45, vendiendo
10 unidades de este lote. El cálculo de la razón
de descuento lo hacemos de la siguiente manera:
![]()

Sustituyendo valores en la fórmula (33)
tenemos:
![]()
Es decir que el porcentaje de rebaja es de 24.32%. Las
razones de descuento son calculados para cada grupo y no
para productos
individuales, al medir la eficiencia relativa de la
mercadotecnia en departamentos, calculamos y comparamos
diferentes periodos. AZY usará razones de rebaja para
juzgar la eficiencia relativa de los clientes y sus vendedores
en los departamentos de la tienda.
5. Las
matemáticas en la investigación de mercados y
muestreo
La investigación de mercados es la
obtención, interpretación y comunicación de información
orientada a las decisiones, la cual será utilizada en
todas las fases del proceso estratégico de
mercadotecnia. Esta definición tiene dos importantes
contenidos:
- Interviene en las tres fases del proceso
administrativo del marketing:
planeación, instrumentación y evaluación. - Reconoce la responsabilidad del investigador de recabar
información útil para los
administradores.
5.1. Alcances
de la investigación de mercado
Dependiendo de sus necesidades y nivel de complejidad,
los directivos de mercadotecnia utilizan cuatro principales
fuentes de
información:
Una es la obtención de reportes
proporcionados regularmente, los cuales son elaborados y
vendidos por empresas de investigación. Éstos son
llamados servicios
sindicados porque son desarrollados sin tener en cuenta a un
cliente en particular, pero son vendidos a cualquier
interesado. Suscribirse a este servicio
permite al empresario
observar regularmente las ventas al detalle de los productos de
sus competidores por tipo de establecimiento y zona
geográfica.
La segunda fuente es el sistema de
información de mercadotecnia, una actividad
interna de una empresa la cual le proporciona un reporte
estandarizado continuo, programado o de flujo de demanda. Los
sistemas de
información de mercadotecnia son utilizados por
directivos y vendedores.
La tercera fuente es el sistema de
apoyo a las decisiones. También es interno, pero
permite a los directivos interactuar directamente con los datos
a través de computadoras
personales para contestar preguntas concretas. Un administrador,
por ejemplo, podría tener un sistema de apoyo a las
decisiones que proporcionará suposiciones
específicas que estimularán el impacto de varios
niveles de publicidad en las ventas de un producto.
La cuarta fuente es un no recurrente y exclusivo
proyecto de
investigación de mercadotecnia, conducido por el
personal de
asesoría de la compañía o por una empresa
de investigación independiente, para contestar una
pregunta específica.
5.2. Excel y las
Funciones
Estadísticas para muestras y
poblaciones
5.2.1. Algunos
conceptos importantes
Antes de pasar a exponer algunas funciones
estadísticas utilizadas en Excel para población y
muestra, desarrollaremos primeramente, conceptos relevantes al
tema que estamos tratando, las medidas centrales como la media
aritmética, mediana, moda y
medidas de dispersión como la desviación media,
desviación estándar y varianza.
Distribución de frecuencia. Ante un gran
número de datos, resulta de mucha utilidad distribuirlos
en clases o categorías y precisar el número de
individuos pertenecientes a cada clase, que
es la frecuencia de clase. La ordenación tabular
de los datos en clases, reunidas las clases y con las
frecuencias correspondientes a cada una, es una
distribución de frecuencias o tabla de frecuencias. La
tabla 1, es una distribución de frecuencias de alturas
(en centímetros) de 1,000 estudiantes
universitarios.
La primera clase o categoría, comprende
las alturas de 150 a 155 centímetros, indicada por el
símbolo 150 – 155. Puesto que 30 estudiantes
tienen una altura perteneciente a esta clase, la
correspondiente frecuencia de clase es 30.
Intervalos de clase y límites
de clase Los intervalos de clase como 150 – 155 de la
tabla anterior, son los intervalos de clase. Los
números extremos, 150 y 155, son los límites
de clase; el número menor 150 es el límite
inferior de la clase y el mayor 155 es el límite
superior. Las denominaciones clase e intervalo de clase son
utilizados indistintamente, aunque el intervalo de clase es
objetivamente un símbolo para la clase.
Marca de clase. La marca de clase
es el punto medio del intervalo de clase, lo obtenemos
sumando los límites inferior y superior de la clase y
dividiendo por 2. Así la marca de clase del intervalo
150 – 155 es (150 + 155)/2 = 152.50 centímetros).
La marca de clase también es conocida como punto
medio de la clase.
Para razonamiento matemático ulteriores, todas
las observaciones pertenecientes a un intervalo de clase dado
lo asumimos como coincidentes con la marca de clase.
Así, todas las alturas en el intervalo de clase 150
– 155 centímetros son considerados como 152.50
centímetros.

Rango. Es la diferencia entre el máximo
y el mínimo valor de la variable o de un conjunto de
números. En la tabla 1, el rango viene dado
así:
![]()
Población, una población es el
total de las observaciones concebibles de un tipo
particular.
Muestra, es un número limitado de
observaciones de una población, elegidos de tal mondo
que permita que todas las observaciones posibles tengan la
misma probabilidad de
presentarse.
5.2.2.
Notación con índice o
subíndice
El símbolo Xj («X sub j») denota
cualquiera de los n valores de X1, X2; X3,…, Xn que una
variable X puede tomar. La letra j en Xj, representa cualquiera
de los números 1, 2,3,…, n, denominado índice o
subíndice. También podemos utilizar como
subíndice cualquier otra letra distinta de j, como i, k,
p, q, s.
El símbolo![]() , indica la suma de todas las Xj desde j = 1 hasta
, indica la suma de todas las Xj desde j = 1 hasta
j = n, es decir, por definición:
![]()
Cuando no cabe confusión posible esta suma esta
representada por las notaciones más simples o. El
símbolo es la letra griega mayúscula sigma,
significando sumación.
![]()

En estos dos ejemplos a es una constante.
Más específicamente.
Ejemplo 3: Si a, b, c son constantes
cualesquiera,
![]()
5.2.4.
Herramientas
de análisis estadístico
Microsoft Excel proporciona un conjunto de
herramientas para el análisis de los datos (denominado
Herramientas para análisis) que podrá utilizar
para ahorrar pasos en el desarrollo
de análisis estadísticos o técnicos
complejos. Cuando utilice una de estas herramientas,
deberá proporcionar los datos y parámetros para
cada análisis; la herramienta utilizará las
funciones de macros
estadísticas o técnicas
correspondientes y, a continuación, mostrará los
resultados en una tabla de resultados. Algunas herramientas
generan gráficos además de tablas de
resultados.
Acceder a las herramientas de análisis de
datos. Las Herramientas para análisis incluyen las
herramientas que se describen a continuación. Para tener
acceso a ellas, haga clic en Análisis de datos en
el menú Herramientas. Si el comando
Análisis de datos no está disponible,
deberá cargar el programa de
complementos de Herramientas para
análisis.
Hay cuatro funciones (VAR, VARP, DESVEST, DESVESTP)
para el cálculo de la varianza y desviación
estándar de los números en un rango de celdas.
Antes de calcular la varianza y la desviación
estándar de un conjunto de valores, es necesario
determinar si esos valores representan el total de la
población o solo una muestra representativa de la misma.
Las funciones VAR y DESVEST suponen que los valores
representan el total de la población.
5.2.4.1.
Medidas de posición central
Son aquellas medidas que nos ayudan a saber donde
están los datos pero sin indicar como se
distribuyen.
La media aritmética o simplemente media, que
denotaremos por, es el resultado obtenido al dividir la suma de
todos los valores de la variable entre el número total
de observaciones, expresada por la siguiente
fórmula:
![]()
Devuelve el promedio (media aritmética) de los
argumentos.
Sintaxis
PROMEDIO(número1;número2;…)
Número1, número2, … son entre 1 y 30
argumentos numéricos cuyo promedio desea
obtener.
Observaciones
- Los argumentos deben ser números o nombres,
matrices o
referencias que contengan números. - Si el argumento matricial o de referencia contiene
texto,
valores lógicos o celdas vacías, estos valores
no son considerados; sin embargo, las celdas con valor cero
son incluidas.
Sugerencia
Cuando calcule el promedio de celdas, tenga en cuenta
la diferencia existente entre las celdas vacías, de
manera especial si ha quitado la marca a la casilla Valores
cero en la ficha Ver (comando Opciones en el menú
Herramientas). Las celdas vacías no se cuentan pero
sí los valores cero.
Ejercicio 03 (Media
aritmética)
¿Cuál será la media
aritmética de los números 10, 5, 8, 14,
13?
1º aplicando la fórmula (28),
tenemos:
![]()
2º Aplicando la función
Promedio de Excel, tenemos:

En el CD que
acompaña la obra, encontrará la solución de
la mayoría de ejercicios en la hoja de Excel. Igualmente,
la mayoría de ejercicios en el CD, contienen etiquetas
explicativas (esquineros de color rojo) del
proceso operativo de las diferentes funciones. Ver la siguiente
ilustración:

La mediana de una serie de datos ordenados en orden de
magnitud es el valor medio o la media aritmética de los
dos valores medios.
Devuelve la mediana de los números. La mediana
es el número que se encuentra en medio de un conjunto de
números, es decir, la mitad de los números es
mayor que la mediana y la otra mitad es menor.
Sintaxis
MEDIANA(número1;número2;
…)
Número1, número2, … son entre 1 y 30
números cuya mediana desea obtener.
Observaciones
- Los argumentos deben ser números o nombres,
matrices o referencias que contengan números. Microsoft
Excel examina todos los números en cada argumento
matricial o de referencia. - Si el argumento matricial o de referencia contiene
texto, valores lógicos o celdas vacías, estos
valores se pasan por alto; sin embargo, se incluirán
las celdas con el valor cero. - Si la cantidad de números en el conjunto es
par, MEDIANA calcula el promedio de los números
centrales.
Ejercicio 02 (Mediana)


La mediana de esta serie es 6.
- Tenemos la siguiente serie:
- Tenemos la siguiente serie:
![]()
![]()

La mediana de esta serie de números es
10:
La moda es el valor de la variable que más
veces se repite, es decir, es el valor más común
o más de moda. La moda puede no existir, incluso si
existe puede no ser única.
Devuelve el valor que se repite con más
frecuencia en una matriz o
rango de datos. Al igual que MEDIANA, MODA es una medida de
posición.
Sintaxis
MODA(número1;número2;
…)
Número1, número2, … son de 1 a 30
argumentos cuya moda desea calcular. También puede
utilizar una matriz única o una referencia matricial en
lugar de argumentos separados con punto y coma.
Observaciones
- Los argumentos deben ser números, nombres,
matrices o referencias que contengan
números. - Si el argumento matricial o de referencia contiene
texto, valores lógicos o celdas vacías, estos
valores se pasan por alto; sin embargo, se incluirán
las celdas con el valor cero. - Si el conjunto de datos no contiene puntos de datos
duplicados, MODA devuelve el valor de error #N/A.
En un conjunto de valores, la moda es el valor que se
repite con mayor frecuencia; la mediana es el valor central y
la media es el valor promedio. Ninguna de estas medidas de la
tendencia central tomada individualmente proporciona una
imagen
completa de los datos. Supongamos que los datos están
agrupados en tres áreas, la mitad de las cuales es un
valor bajo que se repite y la otra mitad consiste en dos
valores elevados. Tanto PROMEDIO como MEDIANA devolverán
un valor situado en una zona central relativamente
vacía, y MODA devolverá el valor bajo
dominante.
Ejemplo 1
La serie: 2, 2, 5, 7, 9, 9, 9, 10, 10, 11, 12, 18
la moda es 9
Ejemplo 2
La serie: 3, 5, 8, 10, 12, 15, 16 no tiene
moda
Ejemplo 3
La serie: 2, 3, 4, 4, 4, 5, 5, 7, 7, 7, 9
tiene dos modas,
por ello es bimodal
5.2.4.2.
La desviación típica y otras medidas de
dispersión
La variación o dispersión de los datos
numéricos es el grado en que estos tienden a extenderse
alrededor de un valor medio. Existen diferentes medidas de
dispersión o variación, las más utilizadas
son el rango (expuesto en el numeral 5.2.1.), la
desviación media, el rango semiintercuartílico,
el rango entre percentiles 10-90 y la desviación
típica.
Cuartiles, Deciles y
Percentiles
Si un conjunto de datos están ordenados
por magnitudes, el valor central (o la media de los dos
centrales) que dividen al conjunto en dos mitades iguales, es
la mediana. Extendiendo esa idea, podemos pensar en
aquellos valores que dividen al conjunto de datos en
cuatro partes iguales. Esos valores denotados por Q1, Q2 y Q3,
son el primer cuartíl, segundo cuartíl y
tercer cuartíl, respectivamente. EL Q2 coincide con
la mediana.
Similarmente, los valores que dividen a los
datos en 10 partes iguales son los deciles,
representados por D1, D2,…,D9, mientras que los valores que
lo dividen en 100 partes iguales son los percentiles, denotados
por P1, P2,…,P99. El 5º decil y el 50º percentil
coinciden con la mediana. Los 25º y 75º
percentiles coinciden con el primer y tercer
cuartiles.
Colectivamente, cuartiles, deciles y percentiles son
los cuantiles.
Las medidas de dispersión tratan de medir el
grado de dispersión que tiene una variable estadística en torno a una
medida de posición o tendencia central,
indicándonos lo representativa que es la medida de
posición. A mayor dispersión menor
representatividad de la medida de posición y
viceversa.
d)
Desviación media absoluta, o promedio de
desviación
Indica las desviaciones con respecto a la media
aritmética en valor absoluto. De una serie de N
números X1, X2,… Xn definido por:
![]()
Donde ![]()
es la media aritmética de los números y ![]() es el valor absoluto de
es el valor absoluto de
las desviaciones de las diferentes ![]() de
de ![]() . Valor absoluto de un número es el mismo
. Valor absoluto de un número es el mismo
número sin signo asociado alguno, representado por dos
barras verticales a ambos lados del número. Así
tenemos:
![]()
Ejercicio 04 (Desviación
media)
Calcular la desviación media de los
números: 4, 5, 8, 10, 13
Solución
1º Calculamos la media aritmética de los
números, aplicando la fórmula (28) y la
función PROMEDIO de Excel:
![]()
2º Aplicando la fórmula (29) y la
función PROMEDIO de Excel, calculamos la desviación
media:
![]()
Si X1, X2;…, Xk presentan con frecuencias f 1,
f2,…, fk, respectivamente, la desviación
media la podemos representar como:
A veces, la desviación media es definida como
desviaciones absolutas de la mediana u otro promedio en lugar de
la media. La desviación media respecto de la mediana es
mínima.
Ejercicio 05 (Desviación
media)
Calcular la desviación media de las siguientes
series de números:
Serie 1: 11, 6, 7, 3, 15, 10, 18, 5
Serie 2: 10, 3, 8, 8, 9, 8, 9, 18
Solución
1º Aplicando la fórmula (28) y la
función PROMEDIO de Excel, calculamos la media
aritmética de cada serie:
1º Calculamos la media aritmética de cada
una de las series aplicando la fórmula (34) y la
función Promedio de Excel:
![]()
![]()

2º Con la fórmula (35) y la función
PROMEDIO de Excel, calculamos la desviación media de cada
una de las series:
![]()
![]()
![]()
![]()
![]()
![]()
Finalmente, la desviación media evidencia que la
serie (2) tiene menos dispersión que la serie
(1).
e)
Desviación típica o desviación
estándar
La desviación estándar es una medida
estadística de la dispersión de un grupo o
población. Una gran desviación estándar
indica que la población esta muy dispersa respecto de la
media; una desviación estándar pequeña
indica que la población está muy compacta
alrededor de la media.
La desviación típica o estándar
para una población puede definirse como:

Donde a es un promedio que puede ser distinto de la
media aritmética. De todas las desviaciones
típicas, la mínima es aquella para la que a =. El
número de elementos de la población esta
representado por N.
Cuando la muestra es pequeña (muestra
propiamente dicha), generalmente es utilizada la siguiente
relación:

Denominada desviación estándar
muestral o desviación estándar
corregida. El número de elementos de la muestra lo
representa n.
Cuando es necesario distinguir la desviación
estándar de una población de la desviación
estándar de una muestra sacada de esta población,
empleamos el símbolo s para la última y
para la primera. Así, s2 y representarán la
desviación estándar muestral y poblacional,
respectivamente.
La varianza mide la mayor o menor dispersión de
los valores de la variable respecto a la media
aritmética. Cuanto mayor sea la varianza mayor
dispersión existirá y por tanto menor
representatividad tendrá la media aritmética. La
varianza se expresa en las mismas unidades que la variable
analizada, pero elevadas al cuadrado.
La varianza de un conjunto de datos se define como el
cuadrado de la desviación estándar y viene dada,
por tanto, por para una población o s2 para
una muestra:
![]()
Cuando la muestra es pequeña (muestra
propiamente dicha), generalmente es utilizada la siguiente
relación:

Denominada varianza muestral o varianza
corregida
5.2.4.3.
Cálculos estadísticos con Excel, con el total de la
población
Si los datos que estamos analizando corresponden al
total de la población en lugar de una muestra, para
calcular la varianza y la desviación típica o
estándar debemos utilizar las funciones VARP y
DESVESTP.
Calcula la varianza en función de toda la
población.
Sintaxis
VARP(número1;número2;
…)
Número1, número2, … son de 1 a 30
argumentos numéricos correspondientes a una
población.
Observaciones
- VARP parte de la hipótesis de que los argumentos
representan la población total. Si sus datos
representan una muestra de la población, utilice VAR
para calcular la varianza. - Utiliza la fórmula (38)
- Se pasan por alto los valores lógicos como
VERDADERO y FALSO y el texto. Si los valores lógicos y
el texto no se deben pasar por alto, utilice la
función de hoja de
cálculo VARP.
Calcula la desviación estándar de la
población total determinada por los argumentos.
La desviación estándar es la medida de la
dispersión de los valores respecto a la media (valor
promedio).
Sintaxis
DESVESTP(número1; número2;
…)
Número1, número2, … son de 1 a 30
argumentos numéricos correspondientes a una
población. También puede utilizar una matriz
única o una referencia matricial en lugar de argumentos
separados con punto y coma.
Se pasan por alto los valores lógicos, como
VERDADERO y FALSO, y de texto. Si los valores lógicos y
el texto no se deben pasar por alto, utilice la función
de hoja de cálculo DESVESTA.
Observaciones
- DESVESTP parte de la hipótesis de
que los argumentos representan la población total. Si
sus datos representan una muestra de la población,
utilice DESVESTP para calcular la desviación
estándar. - Utiliza la fórmula (37)
- Cuando el tamaño de las muestras es
importante, las funciones DESVEST y DESVESTP devuelven
aproximadamente el mismo valor. - La desviación estándar se calcula
utilizando los métodos "sesgado" o "n".
5.2.4.4.
Cálculos estadísticos en Excel con la
muestra
Si los datos que estamos analizando corresponden a una
muestra de la población en lugar de la
población total, para calcular la varianza y la
desviación típica o estándar debemos
utilizar las funciones DESVEST y VAR.
Calcula la desviación estándar en
función de una muestra. La desviación
estándar es la medida de la dispersión de los
valores respecto a la media (valor promedio).
Sintaxis
DESVEST(número1; número2;
…)
Número1, número2, … son de 1 a 30
argumentos numéricos correspondientes a una muestra de
una población. También puede utilizar una matriz
única o una referencia matricial en lugar de argumentos
separados con punto y coma.
Observaciones
- DESVEST parte de la hipótesis de que los
argumentos representan la muestra de una población. Si
sus datos representan la población total, utilice
DESVESTP para calcular la desviación
estándar. - Utiliza la fórmula: (37A)
- La desviación estándar se calcula
utilizando los métodos "no sesgada" o
"n-1". - Se pasan por alto los valores lógicos como
VERDADERO y FALSO y el texto. Si los valores lógicos y
el texto no deben pasarse por alto, utilice la función
de hoja de cálculo DESVESTA.
Calcula la varianza en función de una
muestra.
Sintaxis
VAR(número1;número2;
…)
Número1, número2, … son de 1 a 30
argumentos numéricos correspondientes a una muestra de
una población.
Observaciones
- La función VAR parte de la hipótesis
de que los argumentos representan una muestra de la
población. Si sus datos representan la
población total, utilice VARP para calcular la
varianza. - Utiliza la fórmula: (32A)
- Se pasan por alto los valores lógicos, como
VERDADERO y FALSO y el texto. Si los valores lógicos y
el texto no se deben pasar por alto, utilice la
función de hoja de cálculo VARA.
Ejercicio 06 (Desviación estándar de
una muestra)
Determinar, la desviación típica y la
varianza de cada uno de las series de números del
ejercicio 5.
Para resolver este ejercicio trataremos los datos de las
series como muestra, por cuanto, asumimos como población
el universo de
todos los números enteros. Luego, aplicamos las
fórmulas y funciones de una muestra.
Solución
![]()
1º Calculamos la desviación estándar
de cada una de las series, aplicando la fórmula (37) y la
función DESVEST de Excel:


= 5.15

= 4.16

Comentario
Comparando los resultados con los obtenidos en el
ejercicio 6. Constatamos que la desviación típica
indica que la serie (2) tiene menos dispersión que la
serie (1). No obstante, debemos considerar, el hecho, de que los
valores extremos afectan a la desviación típica
mucho más que a la desviación media. Puesto que las
desviaciones para el cálculo de la desviación
típica son elevadas al cuadrado.
2º Calculamos la varianza directamente elevando al
cuadrado la desviación estándar de cada una de las
series y aplicando indistintamente la función
VAR:
1 = 5.1530; 2 = 4.1555; VAR1 y 2 = ?
![]()
![]()

Ejercicio 07 (Calculando el
rango)
Calcular los rangos de las indemnizaciones recibidas por
cuatro trabajadores de las empresas A y B:
![]()
Rango ( A) = 350 – 90 = 270
Rango ( B) = 235 – 210 = 25 Distribución
menos dispersa
Muchas veces el rango se da por la simple
anotación de los números mayor y menor. En nuestro
ejercicio, esto sería 90 a 350 ó 90-350.
En la Tabla 1, el rango lo calculamos
así:
Rango = Marca de clase de la clase superior – marca de
clase inferior
![]()
Ejercicio 08 (Calculando la media
aritmética)
En la Tabla 1, Tallas de estudiantes universitarios
2004, determinar la marca de clase (x), las desviaciones (d), la
frecuencia (f) y la media aritmética:
Solución
(155 + 150)/2 = 152.50,…, (185 + 180)/2 =
182.50- Calculamos las marcas de
clases aplicando el método
ya conocido: - Tomamos la media supuesta A como la marca de
clase 167.50 (que tiene la mayor frecuencia), podíamos
también tomar cualquier marca de clase. - Calculamos las desviaciones d, restando
de la marca de clase x la media A.
Los cálculos efectuados lo expresamos en la tabla
1-1:
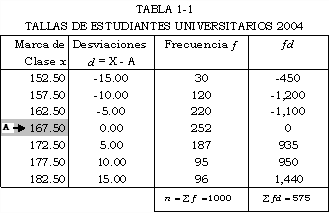
4º Con los datos obtenidos en la Tabla 1, ya
estamos en condiciones de calcular la media aritmética de
la talla de los estudiantes universitarios 2004:
![]()
Ejercicio 09 (Calculando la media
aritmética)
Tenemos la siguiente distribución de frecuencias
de los salarios
semanales en UM de 85 empleados de la empresa BURAN
a.C.:

Determinar el salario medio semanal de los 85
empleados.
Solución
Aplicando los métodos conocidos calculamos la
marca de clase y confeccionamos la siguiente tabla:

Finalmente, calculamos la media aritmética
semanal de los salarios:
![]()
Ejercicio 10 (Desviación
estándar de una población)
Con los valores de la tabla 1, tallas de estudiantes
universitarios 2004, calcular la desviación
estándar:
Solución
Del ejercicio 08, sabemos que la media aritmética
es 168.08 centímetros. Podemos ordenar los datos de la
forma siguiente:

Ahora, vamos a calcular la desviación
estándar:
![]()
Como ya definimos, muestra es el número de
elementos, elegidos o no al azar, tomado de un universo cuyos
resultados deberán extrapolarse al mismo, con la
condición de que sean representativos de la
población.
No es necesario encuestar ni observar a todos los que
pueden arrojar luz sobre un
problema. Basta recabar datos de una muestra, a
condición de que sus reacciones sean representativas del
grupo entero. La clave de la investigación de mercados
es determinar si la muestra suministra suficiente
información.
La idea central en que se fundamenta el muestreo es
que, un número pequeño de objetos (una muestra)
seleccionada adecuadamente de una cantidad mayor de ellos (un
universo) debe reunir las mismas características y casi
en la misma proporción que el número más
grande.
Para conseguir datos confiables, hay que aplicar la
técnica correcta al seleccionar la muestra.
Aunque existen numerosas técnicas muestrales,
sólo las muestras aleatorias o probabilísticas
son adecuadas para hacer generalizaciones de una muestra a un
universo. Extraemos una muestra aleatoria, de modo que
todos los miembros del universo tengan las mismas
probabilidades de ser incluidos en ella.
Las muestras, no aleatorias u opináticas
conocidas con el nombre de muestras disponibles o de
conveniencia, muy comunes en la investigación de
mercados, no los tratamos en presente libro.
Empleando la estadística y
fundamentándonos en la información obtenida por
medio de una muestra, podemos decir cómo es
probablemente una población. Igualmente, podemos tomar
los datos relativos a la población para predecir
cómo deben ser probablemente las muestras. Por
ejemplo, un empresario interesado por el número
de ventas de todas las empresas fabricantes de jeans de la
ciudad de Lima. Puesto que el número de observaciones
posibles es muy grande, debe decidir medir la cantidad de
ventas de 30 de esos establecimientos. En este caso, las 30
empresas son la muestra; la población lo constituyen el
total de las empresas fabricantes de jeans de la ciudad de
Lima.
El empresario, utilizará la
información sobre la muestra para conocer como es
probablemente la población de las empresas fabricantes
de jeans de la ciudad de Lima. Utilizará la
información sobre la población para saber
probablemente como será la muestra. Con esta
información el empresario esta en condiciones de
desarrollar adecuadamente la estrategia de
mercadeo de su
empresa.
Ejemplo 1: Para saber cuál de los
cinco mercados de la zona donde vive Alessandro tiene los mejores
precios,
elabora una lista común de compras y toma los precios que
figuran en la lista, de los cinco mercados. Para conocer si las
cifras obtenidas son muestras o poblaciones, preguntamos
¿Expresan las observaciones todo lo necesario, o asume que
las demás observaciones serán similares?
¿Son poblaciones o muestras las cifras de la lista de
compras?
Respuesta Son muestras. Las poblaciones
son todos los precios de cada almacén;
suponemos que otros días y con otras listas de productos,
obtendremos resultados similares.
Denominamos parámetro, a un
número utilizado para resumir una distribución de
la población. A un número similar, utilizado para
describir una muestra lo denominamos
estadística.
Ejemplo 2 : Estamos estudiamos la
población del Perú y queremos saber si ¿la
edad media de
todos los peruanos es un parámetro o una
estadística?.
Respuesta. Es un parámetro.
Ejemplo 3: Un productor de café de
Jaén, zona nororiental del Perú, desea saber el
número promedio de insectos nocivos a este sembrío
por hectáreas; para ello cuenta el número de
insectos que hay en un gran número de parcelas de una
hectárea, seleccionadas al azar. Preguntamos: ¿El
número de insectos por hectárea que hay en su
muestra es un parámetro o una
estadística?
Respuesta. Es una
estadística.
Finalizando esta parte, precisamos lo siguiente: la
media de una distribución muestral es una
estadística; la media de una distribución de
población es un parámetro; la desviación
estándar de una distribución de la
población es un parámetro y la desviación
estándar de una distribución muestral es una
estadística.
El tamaño de la muestra depende de tres
aspectos:
1) Error permitido
2) Nivel de confianza estimado
3) Carácter finito o infinito de la
población.
Las fórmulas generales para determinar el
tamaño de la muestra son las siguientes:
Para poblaciones infinitas (más de 100,000
habitantes)
![]()
Para poblaciones finitas (menos de 100,000
habitantes)
![]()
Nomenclatura:
n = Número de elementos de la
muestra
N = Número de elementos de la
población o universo
P/Q = Probabilidades con las que se presenta el
fenómeno.
Z2 = Valor crítico correspondiente al nivel
de confianza elegido; siempre se opera con valor zeta 2,
luego Z = 2.
E = Margen de error permitido (determinado por el
responsable del estudio).
Cuando el valor de P y de Q sean desconocidos o cuando
la encuesta
abarque diferentes aspectos en los que estos valores pueden ser
desiguales, es conveniente tomar el caso más adecuado,
es decir, aquel que necesite el máximo tamaño de
la muestra, lo cual ocurre para P = Q =
50, luego, P = 50 y Q =
50.
Ejercicio 11 (Cálculo de la muestra de
una población infinita)
Para un trabajo de investigación de mercados en
el Perú (población infinita 24’000,000 de
habitantes), entre otras cosas, queremos saber cuántas
personas viajarán a trabajar al extranjero, con la
decisión de radicar definitivamente en el país de
destino. ¿Cuál debe ser el tamaño de la
muestra para un nivel de confianza de la encuesta del 95.5% y un
margen posible de error de 4%?
Solución
Z = 2; P = 50; Q = 50; E = 4; n = ?
![]()
![]()
Respuesta:
El tamaño necesario de la muestra para un nivel
de confianza de 4% es 625 personas.
Ejercicio 12 (Cálculo de la muestra de
una población finita)
Para el mismo trabajo de investigación de
mercados en Oyón Perú (población finita
10’000 habitantes), entre otras cosas, queremos saber
cuántas personas viajarán a trabajar al extranjero,
con la decisión de radicar definitivamente en el
país de destino. ¿Cuál debe ser el
tamaño de la muestra para un nivel de confianza de la
encuesta del 95.5% y un margen posible de error de 4%?
Solución
Z = 2; P = 50; Q = 50; E = 4; N = 20,000; n =
?
![]()
![]()
Respuesta:
El tamaño necesario de la muestra para un nivel
de confianza de ![]()
4% es 606 personas.
Ejercicio 13 (Caso integral de
población y muestra con Excel)
Tenemos las ventas mensuales de cinco años de la
empresa BURAN S.A.C., conforme lo ilustramos en el cuadro 14/01,
expresado en unidades monetarias (UM):
CUADRO 14/01

I. Vamos efectuar los cálculos
estadísticos con muestras aplicando las funciones
VAR y DESVEST.
1º Calculamos la media con la función
PROMEDIO, en el cuadro 14/01, seleccionamos las celdas B3:F14 y
obtenemos la media aritmética:
![]()
- = 68,650
2º Confeccionamos el Cuadro 14/02, restando a cada
valor de venta (X) la media de UM 68,650:
CUADRO 14/02

3º Calculamos las funciones VAR y DESVEST, para
ello, en el cuadro 14/02, seleccionamos las celdas B18:E29, que
representan solo una parte de la población:
Las funciones VAR y DESVEST operan con las siguientes
fórmulas:


![]()
Los resultados de las funciones PROMEDIO, VAR y DESVEST
están expresadas en el cuadro siguiente:

Interpretando los resultados y asumiendo que el valor de
las ventas de la empresa BURAN S.A.C., están distribuidas
normalmente, deducimos que aproximadamente el 68% de las ventas
son de:
68,650 – 3,708 = UM 64,942 y
68,650 + 3,708 = UM 72,358
I. Ahora, vamos efectuar los cálculos
estadísticos con el total de la población
aplicando las funciones VARP y DESVESTP. Asumimos que las
celdas B18:E29 del Cuadro 14/02 representan el total de la
población, calculamos la varianza y la desviación
estándar de la población. Operamos con el
promedio, calculado con el total de las ventas.
Las funciones VARP y DESVETP operan con las siguientes
fórmulas:
![]()

![]()
![]()

Como es lógico, los resultados de las funciones
aplicables a muestras son mayores que los obtenidos con las
funciones aplicables a la población total, esto, debido a
que el total de sucesos (n) en el primer caso es (n – 1) y en el
segundo es simplemente (n). Cuanto mayor sea el denominador (n)
menor será el resultado obtenido. Ver aplicación de
funciones Estadística en el CD, que acompaña la
obra.
6. El
Punto de Equilibrio
(Pe)
El análisis de equilibrio es un importante
elemento de planeación a corto plazo; permite calcular
la cuota inferior o mínima de unidades a producir y
vender para que un negocio no incurra en pérdidas.
«Esta herramienta es empleada en la mayor parte de las
empresas y es sumamente útil para cuantificar el volumen
mínimo a lograr (ventas y producción), para alcanzar un nivel de
rentabilidad
(utilidad) deseado. El punto de equilibrio es el punto o
nivel de producción y ventas en el que cesan las
pérdidas y empiezan las utilidades o
viceversa.
Para la determinación del punto de equilibrio
debemos definir y clasificar algunos costos:
Costos fijos: Son aquellos que no varían
con cualquier nivel de producción o ventas.
Costo variable total (CVT). Son los que
cambian proporcionalmente con el nivel de producción o
ventas de una empresa. El costo variable unitario (CVU),
es el valor asociado unitariamente a cada producto o servicio
de la empresa.
Para el cálculo del PE debemos tener en cuenta
las siguientes variables
cantidad producida, precio unitario, costos fijos y costos
variables unitarios. Los ingresos estarán determinados
por la cantidad vendida y el precio de venta unitario, los
costos los determinan la cantidad producida y vendida, los
costos fijos y los costos variables por unidad.
6.1. Punto de
equilibrio en dinero y en unidades
El punto de equilibrio lo podemos calcular en unidades
monetarias o en unidades físicas, conforme veremos en la
solución de los diferentes ejercicios. El cálculo
en unidades monetarias es la recomendada cuando la actividad no
es reconocible en unidades o cuando hay varios bienes o
productos. Aquí interviene mucho la "mezcla de
producto", es decir, la proporción en que son vendidos
los diferentes productos y esta mezcla debe mantenerse
constante en la realidad, para que el punto de equilibrio
calculado coincida con lo real. En los ejercicios que preceden
calcularemos puntos de equilibrio individuales, cuando existen
varios productos.
En caso de calcular el punto de equilibrio en dinero,
tenemos la siguiente expresión:
Ingresos totales = Costos fijos + costos variables
totales
Asumimos que los costos variables unitarios son
proporcionales al precio de venta, luego, así
también lo serán los costos variables totales y
los ingresos totales. En otras palabras, debemos mantener esa
proporción, por lo tanto, podemos escribir la
última expresión de la siguiente
forma:
Ingresos totales = costos fijos + A x (Ingresos
totales)
Donde A es la fracción que representa la
relación entre el costo variable y el precio de venta
(llamado APORTACION).
A = W – CV
La relación de aportación o
BV puede expresarse de diferentes
formas:
![]()
![]()
![]()
La aportación (A) es la diferencia en unidades
monetarias entre el precio de venta y los costos variables o
efectivos. La relación de aportación (BV) es
el porcentaje que representa la aportación con respecto
al precio de venta.
El margen de contribución es el mismo margen
bruto (utilidad bruta expresada como un porcentaje de las
ventas), que estudiamos en la parte concerniente a los ratios
financieros.
Fórmula para calcular el punto de
equilibrio:
A partir de esta fórmula calcularemos el punto
de equilibrio en unidades monetarias, sea con datos totales o
unitarios de los costos variables y ventas. El punto de
equilibrio en unidades físicas lo obtenemos a
través de una simple división del resultado
proporcionada por la fórmula (35) entre el precio
unitario.
![]()
ó ![]()

Otras nomenclaturas utilizadas
PV = Precio de venta del bien o servicio
Q = Cantidad vendida o producida
A = Aportación
BV = Relación de aportación
La fórmula supone que todo lo producido es
vendido, es decir, no va a inventarios. Los productos que
están en inventario tienen costos fijos asignados, que
no se están recuperando (no vendidos) en el momento del
análisis.
Para operar correctamente la fórmula es
necesario que todas las variables estén expresados en la
misma unidad, bien valores monetarios o bien en
unidades.
El punto de equilibrio también sirve para
calcular el volumen de las ventas que debe realizar una empresa
para obtener un porcentaje de utilidad determinado. La
fórmula es la siguiente:
![]()
EJERCICIO 14 (Calculando el Pe de
ventas)
Un pequeño empresario en el ejercicio 2004,
vendió UM 60,000, en el mismo período sus costos
fijos fueron de UM 18,001.29 y los costos variables de UM 32,000.
Calcular el volumen de ventas necesario en punto de
equilibrio.
Solución:
W = 60,000; CF = 18,001.29; CV = 32,000; Pe =
?
![]()
Respuesta:
El nivel necesario de ventas para no ganar, ni perder es
de UM 38,571.44, este es el punto de equilibrio para la
empresa.
Comentario:
El costo fijo permanece invariable, independientemente
del volumen de ventas, mientras que el costo variable está
relacionado directamente con el volumen de ingresos o
ventas.
El porcentaje del costo variable en el punto de
equilibrio está dado por la relación existente
entre los costos variables y el nivel de ventas,
así:
![]()
![]()
Los costos variables en el punto de equilibrio
son:
UM 38,571.43*53.33% = UM 20,570.14

EJERCICIO 15 (Volumen de ventas necesarios
para una utilidad del 30%)
Con los datos del ejercicio anterior determinar el
volumen de ventas necesario para obtener un 30% de utilidad sobre
las ventas en punto de equilibrio.
Solución:
Pe = 38,571; CV = 0.5333; MU = 0.30; W = ?
[42] W = 38,571.43 + 30%(38,571.43) +
53.33%(38,571.43) = UM 70,713.00

Respuesta:
El volumen necesario de venta para obtener un 30% de
utilidad sobre las ventas en punto de equilibrio es UM
70,713.00.
EJERCICIO 16 (Punto de equilibrio en
unidades)
Una empresa con unos costos fijos mensuales de UM
180,000, manufactura un
producto cuyo costo variable de producción es de UM 50 por
unidad y su precio al consumidor es de
UM 200.
Solución:
CF = 180,000; CVU = 50; PV = 250; PE = ?; Q =
?
1º Calculamos el PE en valores
monetarios:
![]()
2º Calculamos la cantidad mensual a
producir:
Q = 225,000/250 = 900 unidades mensuales
Esto quiere decir que si fabricamos y vendemos
más de 900 unidades, el producto generará
utilidades, si fabricamos y vendemos menos de 900 unidades
producirá pérdidas.
Así tenemos, si producimos 1,000 unidades,
tenemos utilidades de:
Utilidad = Ingresos – Costos
UTILIDAD = (250*1000) – (180,000 – (50*1000)) = UM
20,000
Asimismo, si producimos 800 unidades, tenemos
pérdidas por:
PERDIDA = (250*800) – (180,000 – (50*800)) = – UM
20,000
Ejercicio 17 (PE producción y
ventas)
Un pequeño industrial, produce maletines con un
costo de
producción por unidad de UM 10.50 y los vende al por
mayor a UM 15.00, por su local paga la suma de UM 350 más
sus gastos fijos de UM 1,200 mensuales. Determinar cuántos
maletines tiene que producir y vender anualmente para no ganar ni
perder.
Solución:
CF = 1,550; CV = 10.50; W = 15; PV = 15; PE = ?; Q=
?
![]()
Para determinar la cantidad mensual de maletines a
producir, simplemente dividimos el monto obtenido entre el precio
de venta de cada uno:
Q = 5,166.67/15 = 344 maletines de producción
mensual
Calculamos el porcentaje de los costos
variables:
![]()
Comprobando tenemos:

Respuesta:
El pequeño industrial debe producir y vender 344
maletines mensualmente, para no ganar ni perder. Es decir, cuando
produce y vende más de 344 maletines comienzan sus
utilidades.
EJERCICIO 18 (Calculando el Punto de
Equilibrio)
Un pequeño fabricante de gorros cuyo precio
unitario de venta es UM 5, sus costos fijos mensuales son de UM
1,800 y el costo variable unitario es UM 2.80, desea saber el
nivel de producción y ventas que debe tener para no ganar
ni perder.
Solución:
CF = 1,800; CV = 2.80; W = 5; PE = ? Q = ?
1º Calculamos el PE en valores
monetarios:
![]()
2º Calculamos la cantidad mensual a
producir:
Q = 4,000/5 = 800 gorros mensuales
3º Calculamos el porcentaje de los costos
variables:
![]()
Comprobando tenemos:

Respuesta:
La producción y venta necesaria en punto de
equilibrio son 800 gorros equivalentes a UM 4,000
mensuales.
6.2. Punto de
equilibrio para varios productos o servicios
Hasta ahora la técnica de punto de equilibrio
lo utilizamos para determinar a qué nivel de actividad
comienzan las utilidades. Para ello, asumimos que existe un
solo producto, por lo tanto, al calcular la cantidad a producir
en el punto de equilibrio, automáticamente podemos
conocer el valor total de las ventas. Pero en la realidad
tenemos más de un producto o servicio, en este caso no
es tan fácil determinar el punto de equilibrio para la
empresa como un todo. Aquí, cobra preponderancia la
"mezcla de producto", o sea la proporción en que
vendemos los diferentes productos. Si esta proporción no
se mantiene, el punto de equilibrio real se diferenciará
con el proyectado.
EJERCICIO 19 (Punto de equilibrio para varios
productos y servicios)
Un pequeño empresario industrial tiene 2
productos A y B con los siguientes datos:

1º Con esta información estamos en
condiciones de calcular el precio ponderado (PVP) de las ventas
totales y costo Variable unitario (CVUP), de la forma
siguiente:
PVP = (2,350*0.40) + (3,125*0.60) = UM
2,815.00
CVUP = (630 x 0.40) + (1,180 x 0.60) = UM
960.00
2º Con estos resultados ya podemos calcular el
punto de equilibrio total:
CF = 2’900,000; CVU = 960; PVP = 2,815; PE =
?

3º El cálculo del número de unidades
físicas a producir ya no es tan sencillo como cuando
tratamos con un solo producto; una forma sería el
distribuir proporcionalmente los costos fijos a cada producto en
la proporción de la mezcla (A=40% y B=60%). Es así
como calculamos los puntos de equilibrio por producto:
CFA = 0.40 x 2’900,000 = UM
1’160,000
CFB = 0.60 x 2’900,000 = UM
1’740,000
Producto (A)
CF = 1’160,000; CV = 630; PV = 2,350; PE =
?

Producto (B)
CF = 1’740,000; CV = 1,180; PV = 3,125; PE =
?

Finalmente, el punto de equilibrio de la empresa es:(PEA
+ PEB)
674 + 895 = 1,569 unidades
Ejercicio 20 (Punto de equilibrio para varios
productos y servicios)
El precio de venta y el costo variable ponderados, es
válido siempre que mantengamos en la misma
proporción la mezcal de productos en las ventas
totales.
Si la proporción fuera a la inversa en el
ejercicio 20, esto es A=60% y B=40%, entonces los valores
ponderados de precio de venta y costo variable serían los
siguientes:
PVP = (2,350 * 0.60) + (3,125 * 0.40) = UM
2,660
CVUP = (630 * 0.60) + (1,180 * 0.40) = UM
850
El nuevo punto de equilibrio será
entonces:
PVP = 2,660; CVUP = 850; CF = 2’900,000; PE =
?

Calculando el punto de equilibrio en unidades
tenemos:
CFA = 0.60 x 2’900,000 = UM
1’740,000
CFB = 0.40 x 2’900,000 = UM
1’160,000
Producto (A)
CF = 1’740,000; CV = 630; PV = 2,350; PE =
?

Producto (B)
CF = 1’740,000; CV = 1,180; PV = 3,125; PE =
?

Finalmente, el punto de equilibrio de la empresa es:(PEA
+ PEB)
674 + 895 = 1,569 unidades
6.3.
Eliminación de productos o servicios
Existen casos, en el que algunos productos a primera
vista nos dan la impresión de estar produciendo
pérdida, en consecuencia la decisión debe ser
descontinuar su producción.
Esto es cierto, al descontinuar un producto es
reemplazado por otro que absorbe igual o mayor cantidad de
costos fijos.
Tenemos casos en los cuales, al descontinuar un
producto no rentable, su salida afecta el rendimiento de los
demás productos.
Caso 21 (Eliminación de productos y
sevicios)
El dueño de una empresa al ver el cuadro de
producción de su negocio y saber que no era posible
aumentar las ventas del producto B para que produjera utilidades,
comentó que sería prudente descontinuaran la
producción de este producto, pero antes era necesario
analizar la repercusión de esta
decisión.

Procedieron a analizar los efectos de anular la
producción de la línea de productos B y detectaron
lo siguiente:

Al observar los resultados de la tabla anterior
concluimos que el producto B absorbía una buena parte de
los costos fijos, que ahora lo absorben los otros productos. La
decisión no es recomendable.
Ahora, veamos que pasa si descontinuamos la
producción de C:

Ante estos resultados, nos preguntamos:
¿Cuándo debemos eliminar la producción de
un producto?
Esta pregunta es respondida a través de una
adecuada clasificación de los costos fijos:
a) Costos fijos puros o generales y
b) Costos fijos específicos del producto u
operación.
Los costos fijos puros, son aquellos que
cambian, como consecuencia del volumen de la producción,
independientemente de que un determinado producto exista o no.
La depreciación de los equipos y el sueldo del gerente
general, son ejemplos de ello. Los costos fijos
específicos, son aquellos que permanecen constantes
dentro de un rango de operación y son además,
costos fijos asociados de manera específica al producto
o actividad analizados, de manera que si esos productos o
servicios desaparecen, los costos fijos asociados
también desaparecen. Este tipo de costos los constituyen
los gastos de publicidad de un producto en particular, si
desaparece el producto, obviamente desaparece la utilidad.
Aplicando lo expuesto a nuestro caso,
tendríamos:

- Alcaide, Inchausti Angel. 1976. Estadística
Aplicada a las Ciencias
Sociales. Ediciones Pirámide S.A. –
Madrid - Glosario. (2005). Disponible en http://www.worldbank.org – Glosario
- Koosis J., Donald. 1974. Introducción a la Inferencia
Estadística para Administración y Negocios.
Editorial Limusa – México - Kotler, Philip. 1989. Mercadotecnia. Tercera Edición. Prentice-Hall Hispanoamericana
S.A. – México - Leissler Joachim. 1975. Estadística para
Directores Comerciales. Ediciones Pirámide, S.A. –
Madrid - Moya Calderón, Rufino. 1991. Estadística
Descriptiva Conceptos y Aplicaciones. Editorial San Marcos
– Perú - Ruiz Muñoz, David. 2005. Manual de
Estadística. Disponible en http://eumed.net - Spiegel, Murray R. 1970. Serie de Compendio Schaum,
Teoría y Problemas de
Estadística. Libros
McGraw-Hill – México - Tucker A., Sperncer. 1976. El Sistema del Equilibrio.
Instrumento para la planificación de utilidades. Herrera
Hermanos Sucs. S.A. – México - Wonnacott, Thomas H., Wonnaccott Ronal J. 1979.
Fundamentos de Estadística para Administración y
Economía. Editorial Limusa –
México
CESAR ACHING GUZMAN

