15. Amortización
En términos generales, amortización es
cualquier modalidad de pago o extinción de una deuda.
Aquí haremos referencia a la más común de
estas modalidades. La extinción de una deuda mediante un
conjunto de pagos de igual valor en
intervalos regulares de tiempo. En
otras palabras, este método de
extinguir una deuda tiene la misma naturaleza
financiera que las anualidades. Los
problemas de
amortización de deudas representan la aplicación
práctica del concepto de
anualidad.
15.1. Tabla de amortización
La tabla de amortización es un despliegue
completo de los pagos que deben hacerse hasta la extinción
de la deuda. Una vez que conocemos todos los datos del
problema de amortización (saldo de la deuda, valor del
pago regular, tasa de
interés y número de periodos), construimos la
tabla con el saldo inicial de la deuda, desglosamos el pago
regular en intereses y pago del principal, deducimos este
último del saldo de la deuda en el período
anterior, repitiéndose esta mecánica hasta el último
período de pago. Si los cálculos son correctos,
veremos que al principio el pago corresponde en mayor medida a
intereses, mientras que al final el grueso del pago regular es
aplicable a la disminución del principal. En el
último período, el principal de la deuda deber ser
cero.
Estructura general de una tabla de
amortización:
![]()
EJERCICIO 30 (Calculando la cuota uniforme)
La mejora de un proceso
productivo requiere una inversión de UM 56,000 dentro de dos
años. ¿Qué ahorros anuales debe hacerse para
recuperar este gasto en siete años, con el primer abono al
final del año en curso, si contempla una tasa de interés
del 12% anual?
Solución:
VF2 = 56,000; n = 2; i = 0.12; VA = ?;
1º Calculamos el VA de la inversión dentro
de 2 años, aplicando indistintamente la fórmula
(12) o la función
VA:

2º Luego determinamos la cuota periódica
ahorrada a partir de hoy, aplicando la fórmula (19) o la
función pago:
VA = 44,642.86; n = 7; i = 0.12; C = ?

Respuesta:
Los ahorros anuales que deben hacerse son UM
9,782.07
EJERCICIO 31 (Préstamo de Fondo de
Asociación de Trabajadores)
Un sector de trabajadores que cotiza para su
Asociación tiene un fondo de préstamos de
emergencia para los asociados cuyo reglamento establece que los
créditos serán al 9% anual y hasta
36 cuotas. La cantidad de los préstamos depende de la
cuota.
a) Si el préstamo es de UM 3,000
¿cuáles serán las cuotas?
b) Si sus cuotas son UM 120 ¿cuál
sería el valor del préstamo?
Solución (a)
VA = 3,000; n = 36; i = (0.09/12) = 0.0075; C =
?
Para el cálculo de
la cuota aplicamos indistintamente la fórmula (19) o la
función PAGO:

Solución (b)
C = 120; n = 36; i = 0.0075 (0.09/12); VA =?
Para el cálculo de la cuota aplicamos
indistintamente la fórmula (18) o la función
VA:

Respuesta:
(a) Las cuotas serán UM 95.40 y (b) Valor del
préstamo UM 3,773.62
15.2. Sistema de
Amortización Francés
Caracterizado por cuotas de pago constante a lo largo de
la vida del préstamo. También asume que el tipo de
interés es único durante toda la
operación.
El objetivo es
analizar no sólo el valor de las cuotas, sino su
composición, que varía de un período a otro.
Cada cuota está compuesta por una parte de capital y otra
de interés. En este sistema, el valor total de la cuota
permanece constante y el interés disminuye a medida que
decrece el principal. Son útiles las funciones
financieras de Excel para el
cálculo. El interés aplicado es al rebatir, vale
decir sobre los saldos existentes de la deuda en un
período. Muy utilizado por los bancos y tiendas
que venden al crédito.
EJERCICIO 32 (Calculando la cuota mensual de un
préstamo)
Lilian toma un préstamo bancario por UM 3,000
para su liquidación en 6 cuotas mensuales con una tasa de
interés del 4.5% mensual. Calcular el valor de cada cuota
y elabora la tabla de amortización.
Solución:
VA = 3,000; n = 6; i = 0.045; C = ?
1º Calculamos la cuota a pagar
mensualmente:
![]()
2º Elaboramos la TABLA DE AMORTIZACION
FRANCES del préstamo:
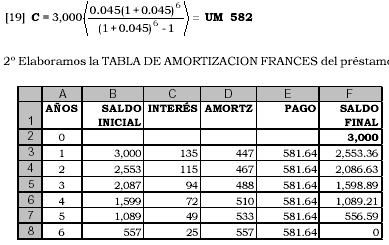
SALDO INICIAL = SALDO FINAL
INTERES = SALDO INICIAL POR TASA DE INTERES
PAGO = FORMULA [19] O BUSCAR OBJETIVO
AMORTIZ. = PAGO – INTERES
SALDO FINAL = SALDO INICIAL – AMORTIZACION
Respuesta:
La cuota mensual a pagar por el préstamo es UM
581.64, contiene la amortización del principal y el
interés mensual.
15.3. Sistema de Amortización
Alemán
Cada cuota está compuesta por una parte de
capital y otra de interés. En este sistema, el valor total
de la cuota disminuye con el tiempo, el componente de capital es
constante, el interés decrece.
No es posible utilizar las funciones financieras de
Excel para su cálculo. Con este método son de mucha
utilidad las
tablas de amortización.
EJERCICIO 33 (Préstamo con amortización
constante)
Una persona toma un
préstamo de UM 4,000 para su liquidación en 24
amortizaciones mensuales iguales, con una tasa de interés
del 3.85% mensual. Calcular el valor de cada cuota y elabore el
cronograma de pagos.
Solución:
VA = 4,000; i = 0.0385; n = 24; C = ?
![]()
Elaboramos el CUADRO DE AMORTIZACION ALEMAN DE LA
DEUDA:

INTERES = SALDO FINAL POR TASA DE INTERES
AMORTIZ. = PRESTAMO / Nº DE CUOTAS
PAGO = INTERES + AMORTIZACION
SALDO FINAL = SALDO INICIAL –
AMORTIZACION
Ejercicios Desarrollados
Interés Compuesto, Anualidades,
Tasas de interés, Tasas Equivalentes
EJERCICIO 34 (Fondo de ahorro)
Durante los 5 años de mayores ingresos de su
actividad empresarial el dueño de una MYPE, ahorra
mensualmente UM 500, colocando el dinero al
8.4% anual en un Banco que
capitaliza los intereses mensualmente. El último abono lo
efectúa el 1º de enero de 1999. A partir de este
momento decide no tocar los ahorros hasta el 1º de enero del
2003. Determinar cuánto es lo ahorrado del 1º de
enero de 1994 al 1º de enero de 1999 y cuánto es lo
que tiene del 1º de enero de 1999 al 1º de enero del
2003.
Solución:
Del 1/1/1994 al 1/1/1999 el caso es de anualidades y del
1/1/1999 al 1/1/2003 es un caso de interés
compuesto.
1) Anualidad: Del 1/1/1994 al 1/1/1999, hay 5
años:
C = 500; i = (0.084/12) = 0.007; n = (5*12) = 60; VF =
?

2) Interés compuesto:
Del 1/1/1999 al 1/1/2003 hay 4 años. El valor
futuro de la cuota periódica es el valor actual para el
cálculo del valor futuro al 1/1/2003:
VA = 37,124.02; n = (4*12) = 48; i = 0.007; VF =
?
[11] VF = 37,124.02 (1 + 0.007)48 = UM
51,888.32

Respuesta: Lo
ahorrado del 1/1/1994 al 1/1/1999 es UM 37,124.02. Lo acumulado
del 1/1/1999 al 1/1/2003 es UM 51,888.32
EJERCICIO 35 (Evaluando el valor actual de un
aditamento)
Un fabricante compra un aditamento para un equipo que
reduce la producción defectuosa en un 8.5% lo que
representa un ahorro de UM 6,000 anuales. Se celebra un contrato para
vender toda la producción por seis años
consecutivos. Luego de este tiempo el aditamento mejorará
la producción defectuosa sólo en un 4.5% durante
otros cinco años. Al cabo de éste tiempo el
aditamento será totalmente inservible. De requerirse un
retorno sobre la inversión del 25% anual, cuánto
estaría dispuesto a pagar ahora por el
aditamento?
Solución
C = 6,000; n = 6; i = 0.25; VA = ?
1º Actualizamos los beneficios de los seis primeros
años:

2º Calculamos el VA de los beneficios para los
próximos 5 años:
Determinamos el monto de la anualidad, aplicando una
regla de tres simple:
![]()
![]()
Con este valor actualizamos la anualidad:
C = 3,176.47; i = 0.25; n = 5; VA = ?

3º Finalmente, sumamos los valores
actuales obtenidos:
VAT = 17,708.54 + 8,542.42 = UM
26,250.96
Respuesta:
El precio a
pagarse hoy por el aditamento con una esperanza de rentabilidad
de 25% anual es UM 26,250.96
EJERCICIO 36 (Calculando la tasa vencida)
Determinar la tasa vencida de una tasa de interés
anticipada de 12% semestral a:
Solución:
ia = 0.12; iv = ?
![]()
Respuesta:
La tasa vencida es 13.64% semestral.
EJERCICIO 37 (Calculando la tasa vencida)
Tenemos una tasa de interés anual de 24%
liquidada trimestralmente por anticipado. ¿Cuál es
el interés trimestral vencido?.

Para utilizar éstas conversiones, trabajar con la
tasa correspondiente a un período de aplicación.
Por ejemplo, una tasa de interés de 12% anticipada y/o
vencida para un semestre.
Respuesta:
La tasa vencida es 6.38% trimestral.
EJERCICIO 38 (Calculando el VF)
Calcular el valor final de un capital de UM 50,000
invertido al 11 % anual, con capitalización compuesta
durante 8 años.
Solución:
VA = 50,000; i = 0.11; n = 8; VF = ?
Calculamos el VF aplicando la fórmula (11) o la
función financiera VF:
VF = 50,000(1 + 0.11)8 = UM
115,226.89

Respuesta:
El valor final o futuro es UM 115,226.89.
EJERCICIO 39 (Calculando n, VF e I)
Un pequeño empresario
deposita UM 1,500 con una tasa del 5% trimestral y
capitalización trimestral el 30 de Marzo de 1999. Calcular
cuánto tendrá acumulado al 30 de Marzo del 2006.
Considerar el interés exacto y comercial.
Solución: Con interés
exacto
VA = 1,500; i = 0.05; n = ?; VF = ?; I = ?
1º Calculamos el plazo (n) con la función
DIAS.LAB (Un año = 365 días y 4
trimestres):

DIAS.LAB/4 = 20.03 n = 20.03
2º Calculamos el VF utilizando la fórmula y
la función respectiva de Excel:

Respuesta:
El monto acumulado después de 20 trimestres es UM
3,985.78
Solución: Con interés
comercial
VA = 1,500; i = 0.05; n = ?; VF = ?; I = = ?
1º Calculamos n aplicando la función
DIAS.LAB:(Un año = 360 días y 4
trimestres)

DIAS.LAB / *4 = 20.31 n = 20.31

Respuesta:
El monto acumulado después de 20.31 trimestres es
UM 4,040.60
Nuevamente, constatamos que el interés comercial
es mayor que el interés exacto.
EJERCICIO 40 (Calculando el VF)
Cuál será el monto después de 12
años si ahorramos:
UM 800 hoy, UM 1,700 en tres años y UM 500 en 5
años, con el 11% anual.
Solución
VA1,3 y 5 = 800, 1,700 y 500; n = 12; i = 0.11; VF12 =
?
Aplicando sucesivamente la fórmula [11] y la
función VF:

Respuesta:
El monto ahorrado después de 12 años es UM
8,185.50
EJERCICIO 41 (Calculando el VF)
Un líder
sindical que negocia un pliego de reclamos, está
interesado en saber cuánto valdrá dentro de 3
años el pasaje, considerando que el aumento en el transporte es
1.4% mensual y el pasaje cuesta hoy UM 1.
Solución:
VA = 1; i = 0.014; n = (12*3) = 36; VF = ?
VF = 1(1 + 0.014)36 = UM 1.65

Respuesta:
Dentro de tres años el pasaje costará UM
1.65
EJERCICIO 42 (Calculando el monto acumulado)
Jorge ahorra mensualmente UM 160 al 1.8% mensual durante
180 meses. Calcular el monto acumulado al final de este
período.
Solución
C = 160; i = 0.018; n = 180; VF = ?
![]()

Respuesta:
El monto acumulado es UM 211,630.87
EJERCICIO 43 (Calculando el plazo)
Durante cuánto tiempo estuvo invertido un capital
de UM 4,800 para que al 12% anual de interés produjera un
monto de UM 8,700.
Solución:
VA = 4,800; i = 0.12; VF = 8,700; n = ?

0.2476*12 = 2.9712 meses 0.9712*30 = 29.1360
días
Comprobando tenemos: (11) VF = 4,800*1.125.2476 =
UM 8,700
Respuesta:
El tiempo en que ha estado
invertido el capital fue de 5 años y 2 meses con 29
días.
EJERCICIO 44 (Calculando el monto final de un
capital)
Qué monto podríamos acumular en 12
años invirtiendo ahora UM 600 en un fondo de
capitalización que paga el 11% los 6 primeros años
y el 13% los últimos 6 años.
Solución:
VA = 600; i6 = 0.11 e i6 = 0.13; n = 12; VF =
?
[11] VF = 600*(1 + 0.11)6*[1 + 0.13)6 = UM
2,336.47

Como apreciamos en la aplicación de la
fórmula los factores de capitalización de cada
tramo no los sumamos sino los multiplicamos. Esto es así
cuando la tasa es variable durante el período de la
inversión y/o obligación.
Respuesta:
El monto acumulado en 12 años es UM
2,236.47
EJERCICIO 45 (Calcular el monto a pagar por una deuda
con atraso)
Un empresario toma un préstamo de UM 18,000 a 12
meses, con una tasa mensual de 3.8% pagadero al vencimiento. El
contrato estipula que en caso de mora, el deudor debe pagar el 4%
mensual sobre el saldo vencido. ¿Calcular el monto a pagar
si cancela la deuda a los doce meses y 25 días?
Solución:
VA = 18,000; n1 = 12; n2 = (25/12) = 0.83; i = 0.038;
imora = 0.04; VF = ?
1º Con la fórmula (11) o la función
VF calculamos el monto a pagar a los doce meses más la
mora por 25 días de atraso:
(11) VF = 18,000(1 + 0.038)12 = UM 28,160.53
(11) VF = 28,160.53(1 + 0.038)0.83 = UM 29,049.46 o
también en un sólo paso:
(11) VF = 18,000*1.03812*1.0380.83 = UM
29,045.88

Respuesta:
La mora es aplicada al saldo no pagado a su vencimiento,
en nuestro caso es UM 28,160.53. El monto que paga al final
incluido la mora es UM 29,096.09.
EJERCICIO 46 (Calculando el tiempo)
Si depositamos hoy UM 6,000, UM 15,000 dentro de cuatro
años y UM 23,000 dentro de seis años a partir del
4to. Año. En qué tiempo tendremos una suma de UM
98,000 si la tasa de interés anual es de 14.5%.
Solución:

1º Capitalizamos los montos abonados hoy (6,000) y
a 4 años (15,000) para sumarlos al abono de UM 23,000
dentro de 10 años, aplicando la fórmula (11)
VF = VA(1 + i)n o la función VF:

2º Calculamos el tiempo necesario para que los
abonos sean UM 98,000:


0.4952*12 = 5.9424 meses 0.9424*30 = 28.2720
días
Tiempo total: 11 años, 6 meses y 28
días
Respuesta:
El tiempo en el que los tres abonos efectuados en
diferentes momentos, se convertirán en UM 98,000 es 11
años, 6 meses y 28 días.
EJERCICIO 47 (Ahorro o inversión)
Hace un año y medio una PYME
invirtió UM 20,000 en un nuevo proceso de
producción y ha obtenido hasta la fecha beneficios por UM
3,200. Determinar a que tasa de interés mensual
debería haber colocado este dinero en una
entidad financiera para obtener los mismos beneficios.
Solución:
VA = 20,000; n = (12*6) = 18; I = 3,200; VF = ?; i =
?
[16] 3,200 = VF – 20,000
VF = 20,000 + 3,200 = UM 23,200

Respuesta:
La tasa necesaria es 0.83% mensual.
EJERCICIO 48 (Sumas equivalentes)
Si UM 5,000 son equivalentes a UM 8,800 con una tasa de
interés
simple anual en tres años; haciendo la misma
inversión con una tasa de interés compuesto del 32%
anual ¿en cuánto tiempo dará la equivalencia
económica?
Solución:
VA = 5,000; VF = 8,800; n = 5; i = ?

Respuesta:
La equivalencia económica se dará en 2
años con 13 días.
EJERCICIO 49 (Calculando el valor de venta de una
máquina)
Una máquina que cuesta hoy UM 60,000 puede
producir ingresos por UM 3,500 anuales. Determinar su valor de
venta dentro de 5 años al 21% anual de interés, que
justifique la inversión.
Solución:
VA = 60,000; C = 3,500; n = 5; i = 0.21; VF1 y 2 =
?
Calculamos el VF del VA de la máquina y de los
ingresos uniformes:
[11] VF = 60,000(1+0.21)5 = UM
155,624.5476

Al VF (155,624.5476) del VA de la máquina le
restamos el VF (26,562.3743) de los ingresos y obtenemos el valor
al que debe venderse la máquina dentro de cinco
años: 155,624.5476 – 26,562.3743 = 129,062.17
También solucionamos este caso en forma
rápida aplicando en un solo paso la función VF,
conforme ilustramos a continuación:

Respuesta:
El valor de venta dentro de cinco años es UM
129,062.17.
EJERCICIO 50 (Evaluación
de alternativas)
Los directivos de una empresa
distribuidora de productos de
primera necesidad desean comprar una camioneta que cuesta UM
22,000, están en condiciones de pagar UM 5,000 al contado
y el saldo en 18 cuotas mensuales. Una financiera acepta 18
cuotas de UM 1,321 y otra ofrece financiar al 4.5%
mensual.
a) ¿Qué interés mensual cobra la
primera financiera?
b) ¿Cuáles serían las cuotas en la
segunda financiera?
c) ¿Cuál financiación debemos
aceptar?
Solución: (a) Primera
financiera
VA = (22,000-5,000) = 17,000; n = 18; C = 1,321; i =
?

Solución: (b) Segunda
Financiera
VA = 17,000; n = 18; i = 0.045; C = ?

Respuestas:
a) El costo efectivo
anual es 56.45%
b) El costo efectivo anual es 69.59%
c) Luego conviene la primera financiera por menor cuota
y menor costo del dinero.
EJERCICIO 51 (Cuota de ahorro mensual para compra de un
carro)
Un empresario desea comprar un automóvil para su
uso personal que
cuesta hoy UM 20,000. Para tal fin abre una cuenta de ahorros que
reconoce una tasa de interés del 1.25% mensual y empieza a
hacer depósitos desde hoy. El carro se incrementa en 15%
anual ¿cuánto deberá depositar mensualmente
para adquirirlo en 5 años?.
Solución:
1º Calculamos el valor del automóvil dentro
de 5 años:
VA = 20,000; i = (0.0125*12) = 0.15; n = 5; VF =
?
[11] VF = 20,000(1 + 0.15]5 = UM
40,227.1437

2º Finalmente, calculamos la cuota
mensual:
VF = 40,227.14; i = 0.0125; n = (5*12) = 60; C =
?

Respuesta:
Para comprar el automóvil dentro de 5 años
al precio de UM 40,227.14; el empresario debe ahorrar
mensualmente UM 461.65.
EJERCICIO 52 (Compra de un computador)
Jorge desea comprar un nuevo computador, para lo cual
cuenta con UM 500, los cuales entregará como cuota
inicial, tomando un préstamo para el resto. El modelo que ha
elegido tiene un valor de UM 2,900, pero el esquema de
financiación exige que tome un seguro que es
1.70% del valor inicial del equipo, el cual puede pagarse en
cuotas mensuales y debe tomarse en el momento de comprarlo.
¿A cuanto ascendería el valor de las cuotas
mensuales para pagar el préstamo en 24 meses con una tasa
de interés del 3.8% mensual?
Costo del equipo UM 2,900.00
(-) Cuota inicial 500.00
Saldo por financiar UM 2,400.00
(+) Seguro por financiar (2,900*1.70%)
49.30
Total por financiar UM 2,449.30
VA = 2,449.30; n = 24; i = 0.038; C= ?
Con estos datos calculamos el valor de cada una de las
cuotas del total por financiar, aplicando indistintamente la
fórmula o la función PAGO de Excel:

Respuesta:
El valor de cada una de las cuotas mensuales es UM
157.37
EJERCICIO 53 (Calculando la cuota mensual por la compra
de un auto)
César compra a plazos un automóvil por UM
15,000 para su pago en 18 cuotas iguales, a una tasa de
interés de 3.5% mensual. Calcular el valor de la
mensualidad.
Solución:
VA = 15,000; n = 24; i = 0.035; C = ?
![]()
Respuesta:
El valor a pagar cada mes es UM 1,137.25. Aplique usted
la función PAGO.
EJERCICIO 54 (Ganaron la Tinka)
Un diario local informa que: «50 personas
comparten el premio mayor de la tinka». Cuenta la historia de 50 trabajadores
que compraron corporativamente un boleto de lotería y
ganaron el premio mayor de UM 5’000,000, al cual era
necesario descontar el 12% de impuesto a las
ganancias ocasionales. Uno de los afortunados trabajadores
coloca sus ganancias a plazo fijo por seis meses al 25% anual con
capitalización semestral. Al cabo de este tiempo tiene
planeado iniciar su propia empresa y
requiere adicionalmente UM 30,000, que los debe cubrir vía
un crédito
al 3.5% mensual y a 36 meses. Determinar el monto para cada uno,
el valor del ahorro a plazo fijo y el monto de las cuotas
mensuales.
Solución: (1)
Premio global UM 5’000,000
(-) 12% Impuesto a las apuestas
600,000
Saldo para distribución entre 50
ganadores UM 4,400,000
Premio para cada uno (4’400,000/50) UM
88,000.00
Solución: (2)
VA = 88,000; n = 1; i = (0.25/2) = 0.125; VF =
?
[11] VF = 88,000[1 + (1*0.125)] = UM
99,000

Solución: (3)
VA = 30,000; n = 36; i = 0.035; C = ?

Respuesta:
1) Monto para cada uno de los ganadores
UM 88,000.00
2) Valor del ahorro a plazo
fijo UM 99,000.00
3) Cuotas mensuales del crédito UM
1,479.52
EJERCICIO 55 (Compra a crédito de un
minicomponente)
Sonia compra un minicomponente al precio de UM 800, a
pagar en 5 cuotas al 5% mensual. Calcular la composición
de cada cuota y elaborar la tabla de
amortización.
Solución:
VA = 800; n = 5; i = 0.05; C = ?
1º Calculamos la cuota mensual:

2º Finalmente elaboramos la TABLA DE AMORTIZACION
SISTEMA FRANCES:

Respuesta:
La cuota mensual es UM 184.78.
EJERCICIO 56 (Compra de máquinas
textiles)
Un pequeño empresario textil adquiere dos
máquinas remalladoras y una cortadora por UM 15,000 para
su pago en 12 cuotas mensuales uniformes. El primer pago se
hará un mes después de efectuada la compra. El
empresario considera que a los 5 meses puede pagar, además
de la mensualidad, una cantidad de UM 3,290 y para saldar su
deuda, le gustaría seguir pagando la misma mensualidad
hasta el final. Este pago adicional, hará que disminuya el
número de mensualidades. Calcular en qué fecha
calendario terminará de liquidarse la deuda, la compra se
llevó a cabo el pasado 1 de Enero del 2003 y la tasa de
interés es 4.5% mensual.
Solución:
VA = 15,000; n = 12; i = 0.045; C = ?
1º Calculamos el valor de cada una de las doce
cuotas:

2º Elaboramos la TABLA DE AMORTIZACION DE SISTEMA
FRANCES:
Al pagar los UM 3,290 adicionales a la cuota del quinto
mes, nos queda un saldo de UM 6,403, como las cuotas mensuales
deben ser de UM 1,644.99, calculamos los meses que faltan hasta
que la deuda quede saldada:
VA = 6,403; i = 0.045; C = 1,645; n = ?


0.37*30 = 11 días
Respuesta:
El pago de la deuda disminuye en casi tres meses, por el
abono adicional en el quinto mes, la obligación es
liquidada el 12/10/2003, siendo la última cuota de UM 609.
La última cuota contiene el saldo final (599) y los
intereses de 11 días.
EJERCICIO 57 (Doble préstamo)
Un préstamo de UM 3,000 a ser pagado en 36 cuotas
mensuales iguales con una tasa de interés de 3.8% mensual,
transcurrido 8 meses existe otro préstamo de UM 2,000 con
la misma tasa de interés, el banco acreedor unifica y
refinancia el primer y segundo préstamo para ser liquidado
en 26 pagos mensuales iguales, realizando el primero 3 meses
después de recibir el segundo préstamo. ¿A
cuánto ascenderán estas cuotas?
Solución:
VA0 = 3,000; VA8 = 2,000; n = 36; n = 26; i = 0.038; C =
?
1º Calculamos cada una de las 36 cuotas con la
fórmula (19) o la función PAGO:

2º En el octavo mes recibimos un préstamo
adicional de UM 2,000 que unificado con el saldo pendiente es
amortizado mensualmente tres meses después de recibido.
Elaboramos la TABLA DE AMORTIZACION DE LA DEUDA.
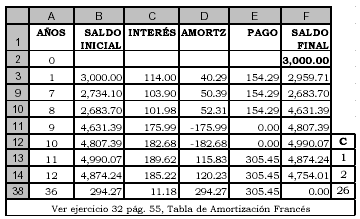
Al momento 8, después de amortizar el principal,
el saldo del préstamo es 2,683.70 – 52.31 = UM 2,631.39
sin embargo, con el nuevo préstamo más los
intereses de los períodos de carencia o gracia el saldo es
de 2,631.39 + 2,000 + 175.99 + 182.68 = 4,990.07 con el que
calculamos el valor de la nueva cuota, aplicando indistintamente
la fórmula [19], la función PAGO o la herramienta
buscar objetivo de Excel:
VA = 4,990.07; i = 0.038; n = 26

Respuesta:
El valor de cada una de las 26 cuotas es UM
305.45
EJERCICIO 58 (Calculando las cuotas variables de
un préstamo)
Tenemos un préstamo de UM 2,500 con una Caja
Rural que cobra el 4.5% de interés mensual, para ser
pagado en 8 abonos iguales. Luego de amortizarse 3 cuotas
negocian con la Caja el pago del saldo restante en dos cuotas, la
primera un mes después y la segunda al final del plazo
pactado inicialmente. Calcular el valor de estas dos
cuotas.
Solución:
VA = 2,500; i = 0.045; n = 8; C = ?
1º Calculamos el valor de cada una de las 8 cuotas,
con la función PAGO:

2º Elaboramos la TABLA DE AMORTIZACION DEL
PRESTAMO, abonado la tercera cuota el saldo del préstamo
es UM 1,663.92. Para el cálculo de la cuota aplicamos
Buscar Objetivo de Excel:

Obtenemos el valor de la amortización 4
dividiendo el saldo pendiente entre 2:
![]()
A este valor adicionar los intereses correspondientes,
incluido los intereses de los períodos de carencia cuando
corresponda.

Respuesta:
El valor de la cuota 4, es UM 906.84
El valor de la cuota 8, es UM 992.13
EJERCICIO 59 (Préstamo sistema de
amortización francés y alemán)
Una persona toma un préstamo por UM 15,000 a
reintegrar en 12 cuotas con un interés del 3.5% mensual.
Aplicar los sistemas de
amortización francés y alemán.
Solución: Sistema
Francés
VA = 15,000; n = 12; i = 0.035; C = ?
1º Calculamos el valor de cada una de las
cuotas:

2º Elaboramos la TABLA DE AMORTIZACION DEL
PRESTAMO, Sistema Francés:

Solución: Sistema
Alemán
VA = 15,000; n = 12; i = 0.035; AMORT. = ?
2º Elaboramos el CUADRO DE AMORTIZACION DE LA
DEUDA, Sistema de Amortización Alemán:

Por falta de espacio hemos ocultado varias filas en cada
cuadro.
Comentario:
En el sistema de amortización francés los
pagos son constantes y la amortización creciente; en el
sistema de amortización alemán los pagos son
decrecientes y la amortización es constante.
EJERCICIO 60 (Préstamo con tasa de interés
flotante)
Un empresario adquiere un préstamo de la Banca Fondista
por UM 5’000,000 a reintegrar en 5 cuotas anuales, con una
tasa de interés flotante que al momento del otorgamiento
es de 5.50% anual. Pagadas las 3 primeras cuotas, la tasa de
interés crece a 7.5% anual, que se mantiene constante
hasta el final.
Solución:
VA = 5’000,000; n = 5; i1…3 = 0.055 y i4…5 =
0.075; i = 0.075; AMORT. = ?
1º Calculamos la amortización
mensual:
![]()
2º Elaboramos el CUADRO DE AMORTIZACION DE LA
DEUDA, Sistema de Amortización Alemán:

Comentario:
Como observamos, el incremento de la tasa de
interés produce un quiebre de la tendencia descendente de
las cuotas. El quiebre tiene su origen en la cuantía de
los intereses.
EJERCICIO 61 (Calculando la tasa efectiva)
Las EDPYMES y Cajas Rurales y Municipales de ahorro y
crédito cobran un promedio anual de 52% por
préstamos en moneda nacional. Calcular la tasa
efectiva.
Solución:
j = 0.52; m = 12; i = ?

Respuesta:
La tasa efectiva anual que cobran estas instituciones
es 66.37%.
EJERCICIO 62 (Calculando la tasa nominal)
Una ONG (como
muchas), canaliza recursos
financieros de fuentes
cooperantes extranjeras para ayuda social. Coloca los recursos
que le envían únicamente a mujeres con casa y
negocio propios al 3.8% mensual en promedio y hasta un
máximo de UM 5,000; además, obligatoriamente los
prestamistas deben ahorrar mensualmente el 15% del valor de la
cuota que no es devuelto a la liquidación del
préstamo, por cuanto los directivos de la ONG dicen que
estos ahorros son para cubrir solidariamente el no pago de los
morosos. Determinar el costo real de estos créditos,
asumiendo un monto de UM 2,000 a ser pagado en 12 cuotas iguales
al 3.8% mensual.
Solución:
VA = 2,000; i = 0.038; n = 12; j = ?; TEA = ?; VF =
?
1º Calculamos la tasa nominal y la TEA del
préstamo:
![]()

2º Calculamos el valor de cada una de las cuotas y
el «ahorro»:

AHORRO MENSUAL OBLIGATORIO= 210.64 * 15% = UM 31.59
mensual
2º Elaboramos la TABLA DE AMORTIZACION DEL
PRESTAMO:

3º Para determinar el costo efectivo del
crédito elaboramos el flujo de
efectivo y aplicamos la función TIR:

4º Calculamos la tasa nominal y la TEA, a partir de
la tasa de interés mensual de 6.28%:

Respuesta:
Considerando el «ahorro» y el valor del
dinero en el tiempo, el costo efectivo del crédito que da
la ONG es de 108.40% anual, que es lo que pagan sus clientes por su
«ayuda social».
EJERCICIO 63 (Evaluando el costo efectivo de un
préstamo)
Un pequeño empresario obtiene un crédito
de una EDPYME por UM 25,000, a una tasa de interés de 52%
anual con capitalización mensual, con una retención
mensual del 1.5% para un fondo de riesgo.
¿Cuál será la tasa efectiva anual y el monto
a pagar transcurrido un año?
Solución:
1º Como la retención es mensual, convertimos
esta tasa periódica a tasa nominal: 0.015*12 = 0.18, luego
sumamos este resultado a la tasa nominal:
j = 52% + 18% = 70% capitalizable
mensualmente:
VA = 25,000; j = 0.70; m = 12; i = ?
2º Calculamos la tasa periódica y efectiva
anual:

3º Finalmente encontramos el monto, transcurrido un
año:
i = (0.9746/12) = 0.0812
[11] VF = 25,000 (1 + 0.0812)12= UM
63,798.79

Respuesta:
La tasa efectiva anual (TEA) es 97.46% y el monto que
paga efectivamente transcurrido un año es UM 63,798.79 por
un préstamo de UM 25,000.
EJERCICIO 64 (Compra con TARJETA de
Crédito)
Una persona con una TARJETA DE CREDITO de una cadena de
SUPER MERCADOS,
adquiere una refrigeradora el 30/12/03 cuyo precio contado es UM
861.54, para ser pagada en 12 cuotas uniformes de UM 96 mensuales
cada una, debiendo agregar a esta cuota portes y seguros por UM
5.99 mensual. El abono de las cuotas es a partir del 5/03/04 (dos
meses libres). Gastos
adicionales UM 17.43 que hacen un total de UM 878.77. Determinar
el costo efectivo y elabore la tabla de amortización de la
deuda.
Solución:
VA = 878.77; n = 14; C = 96; i = ?; TEA = ?
1º Con la función TASA calculamos la tasa
del período ( i ):

2º Con la fórmula [25] calculamos la tasa
nominal:
![]()
3º Con la fórmula [28] o la función
INT.EFECTIVO calculamos la tasa efectiva anual (TEA) de la
deuda:

4º Elaboramos la TABLA DE AMORTIZACION DE LA
DEUDA:

5º Para la determinación del costo efectivo
de la deuda elaboramos el respectivo flujo de
caja:


La cuota mensual que efectivamente paga el cliente es UM
101.99
Respuesta:
El costo efectivo de la deuda incluido los UM 5.99 de
portes y seguro es de 90.22% al año y 5.50%
mensual.
EJERCICIO 65 (Valor actual de los ingresos
anuales)
Una compañía frutera plantó
naranjas cuya primera producción estima en 5 años.
Los ingresos anuales por la venta de la producción
están calculados en UM 500,000 durante 20 años.
Determinar el valor actual considerando una tasa de descuento de
10% anual.
Solución:
C = 500,000; i = 0.10; n = 20; VA = ?
1º Calculamos el valor actual de los 20
ingresos:

2º Finalmente calculamos el valor actual del total
5 años antes de iniciarse la cosecha:
VF = 4’256,781.86; i = 0.10; n = 5; VA =
?

Respuesta:
El valor actual de los 20 ingresos al día de hoy
es UM 2’643,126.62
EJERCICIO 66 (Cuando una inversión se
duplica)
Determinar la conveniencia o no de un negocio de compra
y venta de relojes, que garantiza duplicar el capital invertido
cada 12 meses, o depositar en una libreta de ahorros que paga el
5% anual.
Solución:
VA = 1; VF = 2; n = 12; i = ?
1º Calculamos la tasa de interés de la
operación financiera, cuando el capital se
duplica:

2º Calculamos el valor futuro de los ahorros a la
tasa del 5% anual:
VA = 1; i = 0.05; n = 12; VF = ?

Respuesta:
Es más conveniente la inversión en el
negocio de los relojes.
EJERCICIO 67 (Calculando el valor de contado de un
terreno)
Calcular el valor de contado de una propiedad
vendida en las siguientes condiciones: UM 20,000 de contado; UM
1,000 por mensualidades vencidas durante 2 años y 6 meses
y un último pago de UM 2,500 un mes después de
pagada la última mensualidad. Para el cálculo,
utilizar el 9% con capitalización mensual.
Solución: (i =0.09/12), (n =
2*12+6)
VA1 = 20,000; C1…30 = 1,000; VF31 = 2,500; i = 0.0075;
n = 30; VA = ?
1º Calculamos el VA de la serie de pagos de UM
1,000 durante 30 meses:

2º Calculamos el VA de los UM 2,500 pagados un mes
después de la última cuota:
![]()
Respuesta:
Luego el valor de contado del terreno es: 26,775 + 1,983
+ 20.000 = 48,758
EJERCICIO 68 (La mejor oferta)
Una persona recibe tres ofertas para la compra de su
propiedad:
(a) UM 400,000 de contado;
(b) UM 190,000 de contado y UM 50,000 semestrales,
durante 2 ½ años
(c) UM 20,000 por trimestre anticipado durante 3
años y un pago de UM 250,000, al finalizar el cuarto
año.
¿Qué oferta debe escoger si la tasa de
interés es del 8% anual?
Oferta : UM 400,000
Solución:(b)
i = (0.08/2 semestres) = 0.04; n = (2.5*2) = 5
semestres; VA = ?

Oferta b : 222,591 + 190,000 = UM
412,591
Solución (c):
n = (3*4 trimestres) = 12; i = (0.08/4 trimestres) =
0.02
1º Actualizamos los pagos trimestrales de UM
20,000:

2º Calculamos el VA del último pago anual de
UM 250,000:

Oferta c : 215,737 + 183,757 = UM
399,494
Respuesta:
La oferta (b) es la más conveniente, arroja un
mayor valor actual.
EJERCICIO 69 (Generando fondos para sustitución
de equipos)
¿Qué suma debe depositarse anualmente, en
un fondo que abona el 6% para proveer la sustitución de
los equipos de una compañía cuyo costo es de UM
200,000 y con una vida útil de 5 años, si el valor
de salvamento se estima en el 10% del costo?
Solución:
Valor de salvamento : 200,000 x 10% = 20,000
Fondo para sustitución de equipo: 200,000 –
20,000 = 180,000
Finalmente, calculamos el valor de cada depósito
anual:
VF = 180,000; i = 0.06; n = 5; c = ?
![]()
Respuesta:
El monto necesario a depositar anualmente durante 5
años es UM 31,931.35. Aplique la función PAGO para
obtener el mismo resultado.
EJERCICIO 70 (Sobregiros bancarios)
Por lo general casi todos los empresarios recurren al
banco para cubrir urgencias de caja vía los sobregiros
(ver glosario); los
plazos de éstos dependen de las políticas
de cada institución financiera, pero es común
encontrar en nuestro medio plazos de 48 horas, 3 días como
máximo. Estos plazos casi nunca los cumple el empresario,
normalmente los sobregiros son pagados a los 15 ó 30
días. La tasa promedio para este producto
financiero es 49% anual más una comisión flat de 4%
y gastos de portes de UM 5 por cada sobregiro. Determinar el
descuento, el valor líquido, el costo efectivo de un
sobregiro de 2 días por UM 10,000, los costos cuando
este es pagado con retraso a los 15 y 30 días y la tasa
efectiva anual.
Solución:
VN = 10,000; i = 0.49/360 = 0.0014; n = 2; D2 = ?; VA =
?
1º Aplicando la fórmula (10) calculamos el
descuento del sobregiro para 2 días:

2º Aplicando la fórmula [8] VA = VN –
D, calculamos el VA del sobregiro:
VN = 10,000; D2 = 27.30; iFlat = 0.04; PORTES = 5; VA =
?
(8) VA2 = 10,000 – (27.30 + 5) = 9,967.70 –
(10,000*0.04) = UM 9,567.70
3º Con la fórmula (4A) calculamos la tasa
real de esta operación:
![]()
Hasta esta parte estamos operando con el descuento
bancario a interés simple. El VA obtenido es el valor
líquido o el monto que realmente recibe el empresario.
Pero debe abonar los UM 10,000 a los 2 días, en caso
contrario pagará el interés convencional de 49%
anual, 18% anual de interés moratorio sobre el saldo
deudor (UM 10,000) y UM 5.00 de portes. A partir de este momento
operamos con el interés compuesto.
Sumamos a la tasa de interés los intereses
moratorios:
VA = 10,000; n = 15 y 30; i = (0.49/360 + 0.18/360) =
0.0019; VF =?
4º Calculamos el monto a pagar a los 15 y 30
días incluyendo los portes:
(11) VF = 10,000*(1 + 0.0019)15 + 5 =
10,293.82
(11) VF = 10,000*(1 + 0.0019)30 + 5 =
10,590.99
Luego aplicando la fórmula (13) y la
función TASA, calculamos el costo mensual del
sobregiro:
VA = 9,567.70; n = 15 y 30; VF = 10,293.82 y 10,590.99;
i = ?


5º Finalmente, calculamos la tasa nominal y la TEA
del sobregiro:
(25) j = 0.00339*30* = 1.2204
(28) TEA = (1 + 0.00339)360 – 1 =
2.3816
Respuesta:
1) El descuento para los 2 días es: UM
27.30
2) Los costos cuando el sobregiro es pagado con retraso
son:
Para 15 días = 7.34%
Para 30 días = 10.17%
3) La tasa nominal es : j = 122.04%
La tasa efectiva anual es : TEA = 238.16%
EJERCICIO 71 (Evaluando la compra a crédito en un
supermercado)
Un ama de casa compra a crédito el 8/10/2004 en
un SUPERMERCADO, los siguientes productos:
Una lustradora marcada al contado a UM
310.00
Una aspiradora marcada al contado a UM
276.00
Una aspiradora marcada al contado a UM 115.00 UM
701.00
La señora con la proforma en la mano pide a la
cajera que le fraccione el pago en 12 cuotas iguales con pago
diferido, la cajera ingresa los datos a la máquina y esta
arroja 12 cuotas mensuales de UM 82.90 cada una con vencimiento
la primera el día 5/2/2005. Determine la tasa de
interés periódica y la TEA que cobra el
SUPERMERCADO.
Solución:
VA = 701; C = 82.90; n = 12; i = ?; TEA = ?
1º Aplicando la función TASA calculamos la
tasa periódica de la anualidad:

Tasa mensual = 5.84%

Respuesta:
El SUPERMERCADO cobra mensualmente por sus ventas al
crédito 5.84%, que arroja una tasa nominal de 70.13% y una
Tasa Efectiva Anual de 97.69%. Esta tasa no considera portes,
seguros e Impuesto a las Transacciones Financieras
(ITF).
Por: César Aching
Guzmán
Página personal: http://cesaraching.blogspot.com/
http://es.geocities.com/cesaraching/
Bibliografía
Ayres Franh, Jr. (1971). Serie de Compendio Schaum,
Teoría
y Problemas de Matemáticas
Financieras. Libros
McGraw-Hill – México
2. Aching Guzmán César. (2004). Matemáticas Financieras para Toma de
Decisiones Empresariales. Prociencia y Cultura S.A. –
Perú
3. Biblioteca de
Consulta Microsoft,
Encarta 2003. © 1993-2002 Microsoft
Corporation.
4. Blank T. Leland y Tarquin J. Anthony. (1999).
Ingeniería Económica – IV Edición. Editora Emma Ariza H. –
Colombia
5. Dodge Mark, Stinson Craig. (1999). Running Microsoft
Excel 2000, Guía Completa. McGraw Hill –
México
6. Glosario. (2005). Disponible en http://www.worldbank.org – Glosario
7. Lyman C. Peck. (1970). Matemáticas para
Directivos de Empresa y Economistas. Ediciones Pirámide
S.A. – Madrid
8. Mizrahi Sullivan. (1985). Cálculo con
Aplicaciones a la
Administración, Economía y Biología. UTEHA –
México
9. Moore J.H. (1972). Manual de
Matemáticas Financieras. UTEHA – México
10. Pareja Velez, Ignacio. (2005). Decisiones de
Inversión. Disponible en
http://sigma.poligran.edu.co/politecnico/apoyo/Decisiones/libro_on_line/contenido.html
11. Parkin Michael. (1995). Macroeconomía. Addison – Wesley
Iberoamericana S.A. Wilmington, Delaware, E.U.A.
12. Parkin Michael. (1995). Microeconomía. Addison – Wesley
Iberoamericana S.A. Wilmington, Delaware, E.U.A.
13. Sabino Carlos, (2005). Diccionario de
Economía y Finanzas.
Disponible en http://www.eumed.net/cursecon/dic/
14. Springer, Herlihy y Beggs. (1972).
Matemáticas Básicas, Serie de Matemáticas
para la Dirección de Negocios.
UTEHA – México
15. Van Horne, James C. (1995). Administración Financiera. Décima
Edición. Editorial Prentice Hall, México
Esta obra –como todas mis producciones-
estará difundiéndose gratuitamente en Internet en archivos Word y en
impresión digital PDF, en portales tan importantes
como
gestiopolis.com,
monografías.com, y El
Prisma.com.
La revisión técnica de la obra estuvo a
cargo del Ing. Jorge L.
Aching Samatelo, conforman el equipo de
edición:
COORDINACION GENERAL MARLENE SAMATELO
VALDIVIA
DISEÑO CARATULA ANGELA BONINO
VELAOCHAGA
DISEÑO Y DIAGRAMACION MARIA VICTORIA ANGULO
JOHNSON
PROCESO DIGITAL CESAR ACHING
SAMATELO
PAULA ENITH ACHING DIAZ
 Página anterior Página anterior |   Volver al principio del trabajo Volver al principio del trabajo | Página siguiente  |
