MINITAB – Manual de Entrenamiento

1. Ejemplos y
   ejercicios
2. Prueba T y Pruebas de
   Proporción
4. Regresión
   simple
5. Regresión
   polinomial
6. Regresión
   múltiple
7. Regresiones de los
   mejores subconjuntos
8. El
   análisis de variación
9. Análisis
   de la media
10. Balance
    ANOVA

Ejemplos y
ejercicios

Objetivos

Prueba de Hipótesis

Objetivos

• Prueba de la hipótesis nula utilizando t-test e
  intervalos de confianza.
• Evaluación del Power de la prueba de
  hipótesis
  utilizando el análisis del Power.

Prueba de
Hipótesis

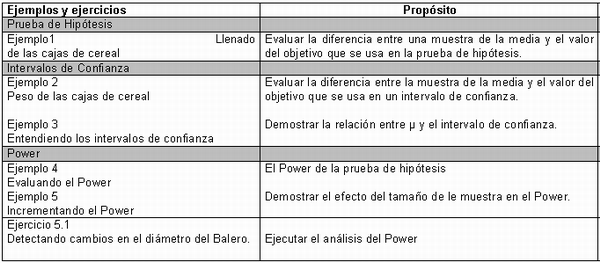
Ejemplo 1 Llenado Cajas de cereal

El propósito de este ejemplo es de introducir los
conceptos de la prueba de hipótesis. Tu usaras un
one-sample t-test para analizar datos procesados
para determinar sí el proceso esta
en el objetivo.

Problema

El objetivo. Tu quieres determinar sí el proceso
esta en el objetivo

Recolección de datos

Para evaluar el proceso de la media. Elegirás 6
cajas de cereal al azar, las pesaras, y usaras los datos de
ejemplo para estimar la media de la población.

Herramientas

Stat> Estadísticas
básicas>1-Sample t

Data set

CEREALBX.MPJ

Prueba de hipótesis

¿Qué es una prueba de
hipótesis?

Una prueba de hipótesis usa datos de ejemplo para
probar una hipótesis acerca de la población de cual
el ejemplo es tomado. El one-sample t-test es uno de los muchos
procedimientos
disponibles para la prueba de una hipótesis en
MINITAB.

Por ejemplo, suponga que quiere probar la medida de las
ruedas del pistón es igual a la longitud deseada del
objetivo. Usted medirá un numero de ruedas y usara la
medida de esas ruedas de ejemplo para estimar la medida de la
rueda de la población. Este es un ejemplo de
stastistical inference, usando información acerca de un ejemplo para hacer
una inferencia acerca de una población.

¿Cuándo usar una prueba de
hipótesis?

Usa una prueba de hipótesis cuando tengas datos
de ejemplo y quieras hacer inferencias acerca de una o más
poblaciones.

¿Por qué usar una prueba de
hipótesis?

La prueba de hipótesis puede ayudar a contestar
preguntas como:

• ¿Esta el proceso correctamente
  centrado?

• ¿Es el producto de
  un proveedor mejor que el producto de otro?

• ¿Hay diferencias entre el tratamiento de los
  grupos y los
  experimentos?

Por ejemplo,

• ¿ Es tu surtido de tu papel en media de 8.5
  pulgadas de ancho?

• ¿La gasolina del proveedor es de mejor
  octanaje que la del proveedor B?

• ¿El cliente
  prefiere una formulación de una bebida sobre
  otra?

Probando la hipótesis nula

Necesitas determinar si la media de un proceso de
empaque
difiere significativamente del peso correcto que es 365 gramos.
En Términos estadísticos, el proceso de la media es
también llamado la población de la
media.

Hipótesis de estadística

Hay 2 posibilidades, µ es igual a 365 o no lo es.
Estas alternativas pueden ser usadas como 2
hipótesis:

• La hipótesis nula (H0): µ es igual a
  .365 gramos

• La hipótesis alternativa(H1): µ no es
  igual a 35 gramos

Por que no puedes medir cada caja en la
población, nunca podrás saber con exactitud cual
hipótesis es correcta. Sin embargo una prueba de
hipótesis apropiada pueda ayudarte a hacer un cálculo
formal. Para estos datos la prueba apropiada es la one-sample
t-test

1- Sample t

1.- Abre el proyecto
CEREALBX.MPJ.

2.- Escoge STAT > Basic
Statistics > 1-Sample t.

3.- Complete el recuadro como se indica a
continuación:

4.- Click OK.

Interpretando tus resultados

La lógica
de la prueba de hipótesis

Todas las pruebas de
hipótesis siguen los mismos pasos:

• Asumir que H0 es verdadera.

• Determinar que tan diferente es tu muestra de lo
  que esperas dado que H0 es verdad.

• Si tu muestra es diferente dado que H0 es verdad,
  entonces descarta H0.

Por ejemplo, los resultados de t-test indican que la
muestra es 366.704. De esta manera el examen contestara la
pregunta, "Si µ es igual a 365, como obtendrás una
muestra de 366.704(o mayor). La respuesta es dada como una
probabilidad
que vale (P), que para esta prueba es igual a 0.143.

Tomando una decisión

Para tomar una decisión, necesitas Escoger el
nivel de importancia, α (alpha), antes de la
prueba:

• Si P es menor o igual a α, rechazas H0
  .
• Si P es mayor que α, si fallas al rechazar H0
  (Tιcnicamente, nunca aceptas H0 ,
  simplemente fallas al rechazarlo).

Un valor
típico para α es 0.05, pero valores
mayores o menores puedes ser escogidos dependiendo de la
exactitud requerida para la prueba. Asumiendo que escojas un
α-Nivel de 0.05 para los datos del peso de la caja no
tendrαs suficiente evidencia para rechazar H0.
P(0.143) es mayor que α.

One-Sample T: Boxweigh

Test of mu = 365 vs not = 365

Variable N Mean StDev SE Mean 95% CI T P

BoxWeigh 6 366.704 2.403 0.981 (364.183, 369.226) 1.74
0.143

Consideraciones finales

Conclusiones prácticas

Basado en tus datos de muestra, no puedes rechazar la
hipótesis nula al 0.05 nivel α. No hay suficiente
evidencia para sugerir que los pesos completos son diferentes a
.365 gramos.

Consideraciones de estadística

Cuando es conducida una prueba de hipótesis,
siempre empiezas con dos hipótesis contrarias:

La hipótesis nula(H0):

• Normalmente dice que si una propiedad de
  una población (tal como la media) no es diferente de un
  valor especifico o de otra población.
• Es asumido que es verdad hasta que tengas suficiente
  evidencia de lo contrario.
• Nunca es aceptado— simplemente fallas al
  rechazarlo.

La hipótesis alternativa(H1):

• Dice que la hipótesis nula esta
  equivocada.
• También especifica la dirección de la diferencia.

Cada prueba de hipótesis esta basada en una o
más suposiciones acerca de los datos que están
analizando. Si esas suposiciones no son conocidas, los resultados
puede que no sean precisos. Las suposiciones de cada prueba
serán exploradas cuando cada prueba sea
discutida.

El Power de una prueba de estadística es la probabilidad de rechazar
correctamente la hipótesis nula. La tabla de abajo muestra
los 4 posibles resultados de la prueba de
hipótesis.

Hipótesis nula

Decisión Verdadero Falso

Falla al rechazar

Rechazar

El nivel α debe ser escogido antes de conducir la
prueba:

• Incrementando α incrementas tus posibilidades
  de detectar una diferencia (y tu Power) pero
  también incrementas la posibilidad de rechazar H0 cuando
  es verdad (error tipo I).
• Disminuyendo α disminuyes tus posibilidades de
  cometer el error tipo I, pero tambiιn
  disminuyes el poder de la
  prueba.

Intervalos de confianza

Ejemplo 2 peso de la caja de cereal

Problema

Recuerde que esta tratando de confirmar que el embalaje
del cereal esté en un objetivo. El objetivo del peso es de
365 gramos y necesitas asegurarte que el proceso de la media
esté dentro de 2.5 gramos que es el objetivo.

Recolección de datos

Seis cajas de cereal fueron elegidas al azar y
pesadas.

Herramientas

Stat > Basic statistics > 1-sample
t

Set de Datos

CEREALBX.MPJ

Intervalos de confianza

¿Que es un intervalo de
confianza?

Un intervalo de confianza es un rango de posibles
valores para un perímetro de una población (tal
como µ) que esta basada en un dato de muestra. Por ejemplo,
muy seguido usaras una muestra para calcular µ. Un
intervalo confidencial te dirá que tan lejos esperes ese
cálculo.

¿Cuándo usar el intervalo de
confianza?

Usa un intervalo de confianza para hacer inferencias de
una o más poblaciones de muestra de datos.

¿Por que usar intervalos de
confianza?

Los intervalos de confianza te pueden ayudar a contestar
muchas de las mismas preguntas de la prueba de
hipótesis:

• ¿Que tan grande podría ser
  µ?
• ¿Qué tan grande podría ser la
  desviación estándar de la
  población?
• ¿Podría µ ser un valor
  cierto?

Por ejemplo,

• Es posible que la longitud de la media de los
  lápices sea mayor a 5.75 pulgadas?
• Podría σ para la longitud de los
  lápices ser tan alto como 0.25 pulgadas?

Usando el intervalo de confianza

En el ejemplo anterior, usamos una prueba de
hipótesis para determinar si la media de tu proceso fuera
diferente al valor del objetivo. También puedes usar un
intervalo de confianza para evaluar ésta
diferencia.

Esta Sesión window resulta para 1-sample t
incluye valores para los fines mayor y menores del 95% del
intervalo de confianza. Obtiene una grafica representativa del
intervalo al seleccionar Boxplot en Graphs subdialog
box.

1-Sample t

1.- Escoge Stat > Basic Statistics >
1-Sample t, or press Ctrl + E.

2.- Click Graphs

3.- Completa el recuadro como se indica a
continuación:

4.- Clik OK en cada recuadro.

Interpretando tus resultados

Intervalo de confianza

El intervalo de confianza es un rango de posibles
valores para µ. Esta mostrado gráficamente como una
línea roja y dos escuadras cuadradas debajo del
boxplot.

Es un intervalo de confianza de 95% por que tomamos 100
muestras de la misma población, los intervalos de 95 de
las muestras incluirá a µ. Por lo tanto para
cualquier ejemplo que pueda ser 95% seguro que la
µ está dentro del intervalo de confianza.

Prueba de hipótesis

El punto rojo de la X representa la media de la muestra
y el punto azul de H0 representa la prueba de la media (365).
Puedes usar el intervalo de confianza para probar la
hipótesis nula:

• Si H0 está fuera del intervalo, la p-value
  para la prueba de hipótesis también será
  menor que 0.05. Puedes rechazar la hipótesis nula en
  α–level 0.05.
• Si H0 esta adentro del intervalo, la p-value
  será mayor que 0.05. No podrás rechazar la
  hipótesis nula en α-level
  0.05.

Por que H0 cae adentro del intervalo de confianza no
puedes rechazar la hipótesis nula. No hay suficiente
evidencia para concluir que µ no es 365 gramos, en el 0.05
nivel significante.

Consideraciones finales

Conclusiones prácticas

El intervalo de confianza de 95% (como el t-test) no
provee suficiente evidencia para rechazar la hipótesis
nula que la población de la media para el peso de las
cajas de cereal sea de 365 gramos.

Consideraciones de Estadística

El intervalo de confianza provee un posible rango
para

valores de µ(u otros parámetros de
población).

En muchos casos, no puedes conducir un prueba de
hipótesis usando un intervalo de confianza. Por ejemplo,
si el valor de la prueba no es entre un 95% de un intervalo de
confianza, puedes rechazar H0 en el nivel α
0.05. Sin embargo si tu estructuras un
99% de intervalo de confianza y no tiene una prueba de la media,
puedes rechazar H0 en el nivel α 0.01.

Intervalos de confianza

Ejemplo 3 Entendiendo los intervalos de
confianza

Problema

Este ejemplo Explora el concepto de las
intervalos de confianza. Simularas la recolección de
muestras al azar para una población normal usando
MINITAB’s generador de números al azar.

Recolección de Datos

Tu debes generar 10 columnas de datos al azar

Herramientas

Calc > Random data > Normal.

Stat > basic Statistics > Display Descriptive
Statistics.

Data set

Ninguno

Generando datos normales al azar

Usando un generado de datos al azar, puedes simular la
recolección
de datos al azar de una población con una media dada.
(Esto es una situación en la cual de hecho puedes saber el
valor de µ.)

Usando el generador de datos al azar para simular la
colección de 10 muestras de una población con una
media(µ) de 10 y de una desviación estándar
de 1. Se generan 20 observaciones para cada muestra.

Normal

1. – Escoge File > New

2. – Selecciona MINITAB Project.

3. – Click OK.

4. – Escoge Calc > Random Data >
Normal.

5.- Completa el recuadro como se indica a
continuación:

6.- Click OK en cada recuadro.

Calculando intervalos de Confianza del
90%

Usa Display Descriptive Statistics para calcular
intervalos de confianza del 90% para cada muestra. Por
definición, 9 de cada 10 intervalos deben contiener la
µ. Desde que sabes que la µ representa muestras que
son iguales a 10, puedes verificar esto directamente.

En contraste a los intervalos de confianza del 95%, los
de 90% son más angostos( esto es que incluyen menos
valores). Porque estos contiene menos valores, es menos probable
que contengan la µ.

Para probar la hipótesis nula que la
µ no es igual a un valor dado, un intervalo de confianza de
90% corresponde a un .10. nivel de α.

Display Descriptive Statistics

1.- Escoge Stat > Basic
Statistics > Graphical Summary.

2.- En Variables, enter
C1-C10.

3.- Completa el Confidence level como se
muestra:

4.- Clik Ok.

Interpretando tus resultados

90% de Intervalo de confianza para Mu
(µ)

Toma un momento para repasar los intervalos de confianza
para cada uno de tus muestras, Las opciones seria que uno de tus
intervalos no va a contener µ(10).

Es posible que todos tus intervalos contengan µ.
También es posible que ninguno lo tenga (aunque es
extremadamente inusual). Sin embargo, si repites el ejercicio de
la generación de muestras al azar y calculando el
intervalo de confianza del 90%, encontraras ese aproximado 90% de
los intervalos que contiene µ.

Resultados hipotéticos

Un ejemplo de un intervalo de confianza de 90% que no
contenga µ es proveído por derecho. El intervalo se
extiende de 10.0275 a 10.7894.

Date cuenta que este ejemplo en particular te
llevará a un rechazo incorrecto de la hipótesis
nula que µ es igual a 10 (asumiendo que
escojas el nivel α de 0.10).

Intervalo de confianza de 90% para
sigma

Date cuanta que la suma gráfica también
incluye a un intervalo de confianza de 90% para σ (la
desviación estándar de la población). El
intervalo tiene en rango de 0.7882 a 1.3501. Si repites este
procedimiento
para un numero largo de muestras, cerca de 9 de 10 intervalos
incluirá el valor para σ.

Estadísticas
Descriptivas

Consideraciones finales

Conclusiones prácticas

Es probable que 1 de 10 intervalos de confianza de 90%
que calcules no contengan µ. Si este procedimiento fuera
repetido para un número largo de muestras, cada 10% de
todos los intervalos confidenciales de 90% no tendrán
µ.

Consideraciones de estadística

Este intervalo de confianza provee un rango de valores
para µ(ó los parámetros de la
población).

En promedio, el 90% de los intervalos de confianza de
90% calculados para muestras al azar tomado de una distribución normal de poblaciones
incluirá a µ.

Power

Ejemplo 4 Evaluando el Power

Ejercicio

No estas seguro que confías en el resultado del
análisis del llenado del peso (página 1-6). Vas a
conducir el análisis del Power para determinar si
recolectaste suficientes datos

Quieres asegurarte que el llenado de las cajas no
difiera del objetivo del peso de 365 gramos no más de 2.5
gramos.

Recolección de datos

Vas a basar el análisis del Power en los
resultados del t-test del ejemplo 1.

Herramientas

Stat> Power and Sample Size> 1-Sample
t

Data set

Ninguno

Análisis del Power

¿Que es un análisis del
Power?

Power es la habilidad de una prueba para detectar un
efecto cuando existe. Cuando conduces una prueba de
hipótesis, hay 4 posibles resultados:

Hipótesis nula

Decisión Verdadero Falso

Falla al rechazar

Rechazar

El Power de la prueba es la probabilidad que rechazara
la hipótesis nula correctamente, dado que la
hipótesis nula es falsa. Puedes usar un análisis
Power para determinar cuanto poder tiene esta prueba, o ayudar a
designar una nueva prueba para que tenga el poder
adecuado.

Cuando usar un análisis del
Power

Usa un análisis del Power cuando estas
diseñando un experimento o después de conducir una
hipótesis nula. No se requieren datos. Necesitaras
estimar σ (excepto por las pruebas de
proporciσn).

¿Por qué usar un análisis del
Power?

El análisis del Power te puede ayudar a responder
preguntas como:

• ¿Es tu muestra lo suficiente
  grande?
• ¿Qué diferencia puedes detectar con tu
  prueba?
• ¿Deberías confiar en los resultados
  insignificantes de la prueba ?

Por ejemplo,

• ¿Cuántas muestras necesitas recolectar
  para determinar si el papel de proveedor es más delgado
  que el de otro por 0.0015 pulgadas?
• ¿Qué tan grande es la diferencia que
  puedes detectar entre la resistencia de
  una viga de acero y un
  historial de la media si reúnes 8 muestras?
• ¿Puedes confiar en los resultados de una
  prueba t-test que indica la resistencia de 2 fórmulas de
  pegamento que no tienen diferencia?

Determinando el Power

Tu meta es determinar que tan ciertos son los resultados
del análisis del llenado de las cajas de cereal
(pagina1-6)

Valores

Si especificas valores para cualquiera de los 2
parámetros de la prueba, MINITAB calculará el
parámetro restante:

• Sample size—– el número de observaciones en
  la muestra
• Differences—– un significado cambio en el
  alejamiento del objetivo que estas interesado en detectar con
  alta probabilidad.
• Power values—– el poder (probabilidad de rechazar
  H0 cuando es falso) que te gustaría que tuviera la
  prueba.

Sigma

Porque el poder de una prueba es parcialmente
determinada por la variabilidad en los datos, debes proveer un
estimado para σ . Usa un estimado del historial o la
desviaciσn estándar de la
muestra.

1. Sample t

1.- Escoge Stat > Power and Sample Size
> 1-Sample t.

2.- Completa el recuadro como se indica a
continuación:

3.- Click OK.

Interpretando tus resultados

Con 6 observaciones, una desviación
estándar de 2.043 y un α de 0.05, el Power solo es
de .5376. Esto significa que µ esta fuera del objetivo por
2.5 gramos, solo tienes un 53.76% de oportunidad para
detectarlo.

De otra manera, hay un 46.24% de probabilidad que falles
al rechazar H0 e incorrectamente concluye que el proceso
está en el objetivo.

¿Qué sigue?

De manera que incrementes tu probabilidad de detectar un
cambio si existe, es incrementar el tamaño de la muestra.
Determinar él numero de observaciones requeridas para
lograr el Power adecuado.

Power and Sample Size

1-Sample t Test

Testing mean = null (versus not = null)

Calculating power for mean = null +
difference

Alpha = 0.05 Assumed standard deviation =
2.403

Determinando el Power

Con 6 observaciones el Power de tu prueba fue solo de
0.5376. Para tener mejores posibilidades de detectar un efecto si
es que existe, deberás incrementar el poder de tu prueba,
que por lo menos sea de 0.80 (como regla general).

Calcular el tamaño de la muestra requerida para
llegar los niveles de Power de 0.80, 0.85, 0.95, y
0.95.

1-Sample t

1.- Escoge Stat > Power and Sample Size
> 1-Sample t.

2.- Completa el recuadro como se indica a
continuación:

3.- Clic OK.

Interpretando tus resultados

Para tener un Power de al menos 0.80 (objetivo del
Power) para detectar una diferencia de 2.5 gramos al nivel
α de 0.05, necesitaras una muestra de
tamaρo 10.

Porque el tamaño de las muestras debe ser siempre
un numero entero. El Power actual de la prueba con 10
observaciones (0.8327) es escasamente mayor que el objetivo
Power.

Observaciones adicionales que dan mas Power:

• Con 11 observaciones, el Power es de
  0.8739.
• Con 12 observaciones, el Power es de
  0.9058.
• Con 15 observaciones, el Power es de
  0.9625.

Al duplicar el tamaño de la muestra de 6 a 12
cajas, incrementas tus posibilidades de detectar una diferencia
de 2.5 gramos (sí es que existe) de 53.76% a
90.58%.

Tal ves no quieran incrementar tu Power demasiado. Si tu
Power es demasiado alto, podrías empezar a detectar
cambios que son demasiado pequeños para ser parcialmente
importantes.

Power and Sample Size

1-Sample t Test

Testing mean = null (versus not = null)

Calculating power for mean = null +
difference

Alpha = 0.05 Assumed standard deviation =
2.403

Power

Ejemplo 5 incrementando Power

Ejercicio

El resultado del análisis de tu Power sugiere que
necesitas una muestra más grande para evaluar tu proceso.
Con solo 6 observaciones, había muy poco Power para
detectar un diferencia de 2.5 gramos

Recolección de datos

12 cajas de cereal son recolectadas al azar y
pesadas

Herramientas

Stat> Basic statistic> 1-sample
t

Data set

CEREALBX.MPJ

Nombre Tipo de dato Tipo de variable

BoxWeigh Numérico Respuesta

Probando la hipótesis nula

Analiza la nueva muestra para determinar si el proceso
de la media es diferente a 365 gramos.

1-Sample t

1.- Abre el proyecto CEREALBX.MPJ.

2.- Escoge Stat> Basic Statistics>
1-Sample t

3.- Completa el recuadro como se indica a
continuación:

4.- Haz clic en Graphs.

5.- Checa Boxplot of data.

6.- Click OK en cada recuadro.

Interpretando tus resultados

El t-test indica que la diferencia entre el
proceso de la media y el objetivo de 365 gramos es significante
en el nivel α 0.05

• El p-value (0.019) es menos que α
  (0.05).
• El intervalo de confianza de 95% no incluye el valor
  del objetivo.

Aparece que las cajas de cereal están siendo
sobre llenadas. Se deben tomar acciones
correctivas para ajustar el proceso.

One-Sample T: MoreObs

Test of mu = 365 vs not = 365

Variable N Mean StDev SE Mean 95% CI T P

MoreObs 12 366.636 2.060 0.595 (365.327, 367.945) 2.75
0.019

Interpretando tus resultados

El boxplot ilustra lo que encontró la
prueba:

• El valor del objetivo(H0) esta afuera del intervalo
  de confianza.
• La muestra de la media (X) es mayor que el valor del
  objetivo.

Conclusión

La diferencia entre el proceso de la media
y el valor del objetivo de 365 gramos es significante en el nivel
α es de 0.05.

Consideraciones finales

Conclusiones prácticas

Es probable que tu primera prueba del llenado de las
cajas de cereal no sea significante porque tu Power era demasiado
bajo. Basado en el numero de observaciones (6), la diferencia que
quieres detectar (2.5), y la variabilidad en los datos, la prueba
tuvo un Power de solo 0.5376.

Usando una muestra grande te da mas Power,
habilitándote para detectar la diferencia.

Consideraciones estadísticas

Para asegurar que tu prueba tenga suficiente Power, es
una buena idea el conducir un análisis power para
recolectar datos.

Las maneras de incrementar el Power de una prueba
incluye:

• Incrementar el tamaño de la
  muestra.
• Disminuir la variabilidad que no esta atribuida al
  efecto de interés.
• Incrementar α (aunque esto
  tambiιn te llevara a incrementar un error del
  tipo I).

Mayor Power significa una mayor probabilidad de detectar
los errores. Sin embargo también incrementa la
probabilidad de detectar errores pequeños que puede que no
sean de interés. El proceso del conocimiento
ayuda a determinar el nivel optimo del Power en una
prueba.

Ejercicio 5.1 Detectando posibilidades en el
diámetro de un balero

Ejercicio

Una parte del Balero manufacturado está fuera de
especificaciones 0.05 cm de lo correcto. Un cambio de 0.01cm es
considerado lo suficientemente importante para permitir el ajuste
al equipo.

La desviación estándar de los
diámetros es casi siempre de 0.004 cm.

Recolección de datos

Ninguno

Instrucciones

2. Use Stat > Power and sample size > 1-sample
   t para calcular el tamaño de la muestra necesitaras
   detectar una diferencia de 0.01cm con el Power de 0.85 en un
   nivel α de 0.05
3. Calcular las diferencias puedes detectarlas con un
   power de 0.90 cuando recolectes 5 y 10
   observaciones.

Data set

Ninguno

Power and Sample Size

1-Sample t Test

Testing mean = null (versus not = null)

Calculating power for mean = null +
difference

Alpha = 0.05 Assumed standard deviation =
0.05

Power and Sample Size

1-Sample t Test

Testing mean = null (versus not = null)

Calculating power for mean = null +
difference

Alpha = 0.05 Assumed standard deviation =
0.05

Sample

Size Power Difference

5 0.9 0.0982944

Power and Sample Size

1-Sample t Test

Testing mean = null (versus not = null)

Calculating power for mean = null +
difference

Alpha = 0.05 Assumed standard deviation =
0.05

Sample

Size Power Difference

10 0.9 0.0577282

PRUEBA T Y PRUEBAS DE
PROPORCIÓN

Objetivos

• Evaluar la diferencia entre la media del proceso y
  un valor de un objetivo usando un One-Sample
  t-test.
• Evaluar la diferencia entre 2 muestras de la media
  usando en Two-Sample t-test.
• Evaluar las diferencias entre 2 observaciones
  usando un Paired t-test.
• Evaluar la diferencia entre una proporción
  y un valor de un objetivo usando una prueba de una
  proporción.

Contenidos

One-Sample t-Test

Ejemplo 1 Problema del Gran Queso

Ejercicio

Tu compañía, El Gran Queso, Inc., sospecha
que uno de tus proveedores de
leche le esta
añadiendo agua a su
leche para incrementar sus beneficios. Añadir agua a la
leche incrementa su punto de congelación, que normalmente
es de –0.545º C.

Recolección de datos

El punto de congelación es medido para 10
muestras al azar de la leche del proveedor.

Herramientas

Stat> Basic Statistics> Normality
Test.

Stat> Basic Statistics> 1-Sample
t.

Data set

CHEESE.MPJ

One-Sample T: FrzTemp

Variable N Mean StDev SE Mean 95% CI

FrzTemp 10 -0.539368 0.007799 0.002466 (-0.544947,
-0.533790)

One-sample t-test

¿Qué es un One-Sample
t-test?

Un One-Sample t-test te ayuda a determinar si µ
(la población de la media) es igual a un valor d una
hipótesis (la prueba de la media).

La prueba utiliza desviaciones estándar de una
muestra para estimar σ (la
desviaciσn estándar de la
población). Si la diferencia entre la muestra de la media
y la prueba de la media es grande relativamente a la variabilidad
en la muestra, entonces µ es improbable que sea igual a la
prueba de la media.

¿Cuándo usar un one-sample
t-test?

Usa un one-sample t-test cuando tienes datos continuos
de una sola muestra al azar.

La prueba asume que la población esta distribuida
normalmente. Sin embargo es muy justo a las violaciones de esta
suposición, proveídas las observaciones son
recolectadas al azar y los datos son continuos y racionalmente
simétricos. (ver Box, Hunter & Hunter (1978).
Statistics for Experimenters, John Wiley & Sons,
Inc.).

¿Por qué usar un one-sample
t-test?

Un one-sample t-test te puede ayudar a responder
preguntas tales como:

• ¿Esta el proceso en el objetivo?
• ¿El producto de tu proveedor cumple con tu
  criterio?

Por ejemplo,

• Es el ancho de la media de las navajas mayor o menor
  que el objetivo?
• Es la resistencia de la media de los tornillos de tu
  proveedor menor de lo requerido?

Guías al Escoger las Herramientas
de Estadística

Tipo de Variable de
Respuesta

Probando la suposición de una
normalidad

La prueba de Estadística apropiada para los datos
de la temperatura
congelante es un one-sample t-test. Esta prueba asume que la
población esta normalmente distribuida.

Usa una prueba de normalidad para determinar si la
suposición de la normalidad es valida para esos
datos.

Prueba de normalidad

1. Abre el proyecto CHEESE.MPJ
2. Elige Stat> Basic statistics> Normality
   Test

   

3. Completa el recuadro como se indica a
   continuación:
4. Haz clic en OK

Interpretando tus resultados

Usa el normal probability plot para verificar que tus
datos no se desvíen significativamente de una
distribución normal.

• Si los datos vienen de una distribución
  normal, los puntos muy apenas seguirán la línea
  de referencia.
• Si los datos no vienen de una distribución
  normal, los puntos no seguirán la
  línea.

Anderson-Darling normality test

Un p-value de Anderson-Darlin Test (0.0352) accesa a la
probabilidad que los datos son de una población con
distribución normal. Usando en α de 0.05, no hay
suficiente evidencia para sugerir que los datos no son de una
población normal.

Conclusión

Basado en el argumento y en la prueba es razonable
asumir que tus datos no se desvían substancialmente de una
distribución normal. Puedes proceder con el
t-test.

Conduciendo el 1-sample t-test

Conducir un 1-sample t-test para determinar si la
temperatura congelante de la leche del proveedor es mayor a
–0.545º C.

No hay razón para sospechar que el proveedor
quitara el agua de la
leche. Así, no necesitas probar si la temperatura
congelante es menor que –0.545º C. En esta
situación, puedes usar una prueba 1-tailed (en la cual H1
es direccional):

• H0 :µ = -0.545
• H1 :µ > -0.545 (En una prueba 2-tailed, H1
  No es direccional: µ es diferente a
  –0.545)

La ventaja de la prueba 1-tailed es que te da mas Power
para detectar la diferencia especificada. Sin embargo, una prueba
1-tailed no puede detectar una diferencia en la dirección
contraria que especifica en H1. De esta manera si hay diferencias
en ambas direcciones son de interés, deberás usar
una 2 tailed test.

1-Sample t

2. Escoge Stat> Basic Statistics> Sample
   t.
3. Completa el recuadro como se indica a
   continuación:

2. Haz click Options.
3. De Alternative, Escoge greater
   than.
4. Click OK en cada recuadro.

Interpretando tus resultados

Usa un nivel α de 0.05 para la prueba.

T

El t-statistic (2.28) es calculado de esta
manera:

T = (muestra de la media – prueba de la media) /
SE media

Donde SE media es el error estándar de la media
(una medida de variabilidad). Como el valor de t se incremente,
el p-value se hace mas pequeño.

P

El p-value es 0.024. Porque este valor es menor que
α(0.05), puedes rechazar la hipσtesis
nula. El resultado sugiere que el agua o cualquier otro liquido
halla sido añadido a la leche.

Power

Cuando sea apropiado, una prueba 1-tailed es mas
poderosa que una prueba 2-tailed. Por ejemplo, una prueba
2-tailed (H1 : µ es diferente a –0.545) regresa a
p-value de 0.048, que es mayor que 0.024.

One-Sample T: FrzTemp

Test of mu = -0.545 vs > -0.545

Consideraciones finales

Conclusiones prácticas

El 1-tailed, 1-sample t-test sugiere que la temperatura
congelante de la leche del proveedor es mayor a la que debe ser,
indicando que se le pudo haber añadido agua. Esta es una
acusación muy seria para el proveedor. Podría ser
mejor evaluar que tan cierto es antes de tomar una
decisión.

Con un nivel α de 0.05, las probabilidades de
haber concluido que se le ha aρadido agua cuando
no es así son de 5%. Para estar seguro que no rechaces H0
incorrectamente, deberás Escoger valores menores para
α, tales como 0.01 o hasta 0.001. Con un
α de 0.01, no concluirαs que se le
allá añadido agua a la leche (p =
0.024).

Consideraciones estadísticas

Cuando uses una 1-sample t-test:

• Tu muestra debe de ser al azar.
• Los datos de muestra deben de ser continuos
  .
• Los datos de muestra deben de distribución
  normal.

Debe de ser notado que los procedimientos del t-test son
muy justas a las violaciones de las suposiciones de normalidad,
dadas esas observaciones son recolectadas al azar y los datos son
continuos y racionalmente simétricos. (ver Box, Hunter
& Hunter (1978). Statistics for Experimenters, John Wiley
& Sons, Inc.).

Una prueba 1-tailed es mas poderosa que una prueba
2-tailed. A menos que la diferencia no este en la
dirección esperada, Por ejemplo una prueba 1-tailed con
una hipótesis alternativa, H1 : µ > -0.545 nunca
será capaz de detectar la diferencia si alguien disminuye
la temperatura congelante de la leche.

Ejercicio 1.1 Diámetro de los Valeros de
Bola

Ejercicio

Tu compañía produce Valeros de bola y
necesitas verificar que el tamaño del Balero que
esté en las especificaciones. La especificación del
diámetro para los Valeros es de 0.5cm.

Usa un nivel α de 0.05 para todas las
pruebas.

Recolección de datos

10 Valeros son escogidos al azar y medidos.

Instrucciones

2. Prueba la muestra de normalidad usando Stat>
   Basic Statics> Normality Test.
3. Usa Stat> Basic Statistics> 1-sample t
   para determinar si el proceso esta en el objetivo. Conduce
   una prueba 2-tailed (H1 : µ es diferente a 0.5) y crea
   un boxplot de los datos.
4. Usando la desviación estándar de la
   muestra como un estimado de σ, ¿cuál es
   el Power de la prueba para detectar una diferencia de
   0.005cm.?
5. ¿Cuál es el tamaño
   mínimo para la muestra requerida para detectar la
   misma diferencia con un Power de 0.80?

Data set

BEARINGS.MPJ

Two-Sample t-Test

Ejemplo 2 Resistencia plástica

Ejercicio

Tu compañía hace estuches de plástico
para calculadoras. Necesitas comparar muestras de plásticos
de 2 proveedores en cuanto a su resistencia. El proveedor A dice
tenar el plástico mas fuerte, pero cuesta mas que del
proveedor B.

Recolección de datos

Pellets seleccionadas al azar de un grupo de
plástico son prensadas en agua hasta ser barquillas del
mismo grueso. La resistencia para romperlos( en psi, libra por
pulgada cuadrada) es tomada para cada barquilla.

Herramientas

Stat> Basic Statistics> Normality
Test

Stat> Basic Statistics> 2
variances

Stat> Basic Statistics> 2-sample
t

Set de Datos

PLASTIC.MPJ

Two-sample t-test

¿Qué es un two-sample
t-test?

Una two-sample t-test te ayuda a determinar si 2
poblaciones de la media son iguales.

La prueba usa las desviaciones estándar de la
muestra para estimar σ para cada
población. Si la diferencia entre la muestra de la media
es grande relativamente para la variabilidad estimada entre las
poblaciones, entonces la media de la población son
improbables a ser iguales.

Un two-sample t-test también te puede ayudar a
evaluar si la media de 2 poblaciones es diferente por una
cantidad especifica.

¿Cuándo usar una prueba two-sample
t-test?

Usa una prueba two-sample t-test cuando tengas datos
continuos de 2 muestras al azar independiente. Las muestras son
independientes si las observaciones de un one.sample no
están relacionadas a las observaciones de la otra muestra.
Por ejemplo, 2 medidas son tomadas por un mismo operador no son
independientes.

La prueba también asume que tus datos vienen de
una población normalmente distribuida. Sin embargo es muy
justo hacia las violaciones de esta suposición
proveídas las observaciones son recolectadas al azar y los
datos son continuos y razonablemente simétricos. (ver
Box, Hunter & Hunter (1978). Statistics for Experimenters,
John Wiley & Sons, Inc.).

¿Por que usar una prueba two-sample
t-test?

Un two-sample t-test te puede ayudar a contestar
preguntas tales como:

• ¿Son los productos de
  dos proveedores comparables?
• ¿Es la formula de un producto mejor que el
  otro?

Por ejemplo,

• ¿Es similar la viscosidad del
  aceite de
  dos proveedores?
• ¿Es la formula de una tinta más
  brillante que otra?

Probando las suposiciones de la
normalidad

La prueba de estadística mas apropiada para los
datos del proveedor es la two-sample t-test. Esta prueba asume
que los datos son de poblaciones distribuidas
normalmente.

Usa la prueba de normalidad para determinar si la
suposición de la normalidad es valida para estos
datos.

Prueba de normalidad

1. Abre el proyecto PLASTIC.MPJ.
2. Escoge Stat> Basic statistics> Normality
   Test.
3. En Variable, enter ´SupplrA´.
4. Click OK.
5. Escoge Stat > Basic Statistics > Normality
   Test, or press ctrl. + E.
6. En Variable, enter ´SupplrB.
7. Click OK

Interpretando tus resultados

Usa la normal probability plot para verificar que tus
datos no se desvíen significativamente de una
distribución normal.

• Si los datos vienen de una distribución
  normal, los puntos muy apenas seguirán la línea
  de referencia.
• Si los datos no vienen de una distribución
  normal, los puntos no seguirán la
  línea.

El plot para el SupllrA indica que la
distribución de la muestra es razonablemente normal; todos
los puntos están cerca de la línea.

El plot para el SupplrB sin embargo aparentemente
muestra desviación de la normalidad.

Anderson-Darling Normality test

La desviación de la normalidad observada de
SupplrB no es significante en un nivel α de
0.05. Ambas p-values(0.664 para SupplrA, y 0.083 para SupplrB)
son mayor que 0.05.

Conclusión

Basado en el plot y las pruebas, es racional asumir que
tus datos no se desvían substancialmente de una
distribución normal. La suposición de una
normalidad es relativamente satisfecha, así que puedes
proceder con el t-test.

Comparando las variaciones

Antes de conducir el t-test, debes evaluar las
variaciones de las 2 distribuciones para ver si difieren. Hay dos
razones para esto:

• Es importante saber sí el producto de un
  proveedor varia mas que el del otro
• Los cálculos para el two-sample t-test depende
  si las variaciones de las muestras son iguales o
  diferentes.

Para asegurar que encontraste una diferencia entre 2
variaciones si es que existe una. Debes usar un nivel
α de 0.10 para esta prueba en lugar de la normal de
0.05. Esto incrementara el power de la prueba.

2. 2. Escoge Stat> Basic statistics> 2
      Variances.
   3. Completa el recuadro como se indica a
      continuación:
3. Variances

4. Click Options.
5. En Confidence level, enter 90.
6. Click OK en cada recuadro.

Interpretando tus resultados

Intervalos de confianza

Los intervalos de confianza son útiles para
comparar σ de las 2 poblaciones.
Sin embargo, tu decisión acerca de sí las 2
variaciones son iguales será basadas en una apropiada
prueba de variación.

Pruebas de variación

Los resultados incluyen 2 pruebas de variación
separadas. El uso de la prueba depende de tus datos.

• Si tus datos son continuos y de distribución
  normal, usa el F-test.
• Si tus datos son continuos pero no necesariamente de
  distribución normal, usa el Levene`s test.

Los datos dados son racionalmente normales, así
que puedes usar el F-test. Sin embargo, porque el p-value de la
prueba de normalidad del proveedor B fue muy baja (0.083), hay
que revisar los resultados de la prueba de Levene`s
también.

Conclusión

Los p-values para ambos F-test (0.067) y la Levene`s
(0.052) son menos que α (0.10), asν
que puedes rechazar la hipótesis nula que las
variaciones son iguales. Los resultados sugieren que las
variaciones del plástico del proveedor A son más
pequeños que las del proveedor B.

F-Test (normal distribution)

Test statistic = 0.28, p-value = 0.067

Levene's Test(any continuous distribution)

Test statistic = 4.27, p-value = 0.052

Test for Equal Variances for SupplrA,
SupplrB

Interpretando tus resultados

Los mismos intervalos de confianza y las pruebas
estadísticas incluidas en la ventana de resultados de la
grafica también son proveídas en la ventana de
sesión.

Test for Equal Variances: SupplrA,
SupplrB

95% Bonferroni confidence intervals for standard
deviations

F-Test (normal distribution)

Test statistic = 0.28, p-value = 0.067

Levene's Test(any continuous distribution)

Test statistic = 4.27, p-value = 0.052

Conduciendo el Two-Sample t-test

Por que los datos son razonablemente normales, tu puedes
usar 2 Sample t -to test ya sea la resistencia del
plástico de los dos diferentes proveedores.

La prueba de Hipótesis es:

• H0 : µ A – µ B = 0
• H1 : µ A – µ B ≠ 0

Elabora dotplots y boxplots para ayudar a visualizar los
datos.

Asumir discrepancias desiguales

Si asumes que las varianzas de las dos poblaciones son
iguales, tu t-test será más confiable. Sin embargo,
si asumes que la varianza es igual cuando no lo son, los
resultados de tu t-test serán falsos. Así, si hay
alguna duda, es mejor no asumir que son iguales.

Porque la variance test indica que la población
de la varianza es diferente, no asuma que las varianzas son
iguales.

2-Sample t

2. Escoge Stat > Basic Statistics > 2-Sample
   t.
3. Complementa el recuadro como se indica a
   continuación:

4. Click Graphs.
5. Revisa Dotplots of data y Boxplots of
   data.
6. Click OK en cada recuadro.

Interpretando los Resultados

Las gráficas ilustran dos puntos :

• El plástico del proveedor A se muestra
  más resistente que el del proveedor B.
• Hay mas variabilidad en la resistencia del
  Plástico del Proveedor B que del Proveedor
  A.

Interpretando tus Resultados

Two-Sample T-Test and CI: SupplrA,
SupplrB

Two-Sample T-Test and CISupplrA,
SupplrB

Individual Value Plot of SupplrA,
SupplrB

Boxplot of SupplrA, SupplrB

El promedio del punto de quiebre del plástico
(media) y dos medidas de la variabilidad—la
desviación estándar (StDev) y el error
estándar de la media (SE Mean)—se presentan en cada
Proveedor.

Intervalos de Confianza

La diferencia entre la muestra de la media (7.484) se
utiliza para estimar la diferencia entre la población de
la media (mu SupplrA—mu SupplrB). El intervalo de confianza
por la diferencia se basa en esta estimación y la
variabilidad de las muestras.

Puede ser 95% confiable que la diferencia entre la
población de la media es entre 6.687 y 8.281
psi.

T-value y p-value

El T-value para la prueba es 19.82, lo cual se asocia
con un p-value menor que 0.0005 (lo cual se redondea a
0.000)

Así, puedes rechazar la Hipótesis nula en
0.05 α-level, donde concluye que las resistencias
son diferentes.

Consideraciones finales

Conclusiones prácticas

El proveedor de plástico A es significativamente
resistente y menos variable que el proveedor B. Sin embargo,
observamos que el Proveedor A también nos cobra mas por el
producto. Ahora tienes que decidir si la diferencia entre los
Proveedores es significativa.

Se cuenta con el 95% de confianza de la verdadera
diferencia entre el proveedor 6.687 y 8.281 psi. Tu decides pagar
o no un precio alto
por una pequeña diferencia en la resistencia.

Consideraciones estadísticas

Cuando utilizas two-sample t-test :

• Las muestras deben ser al azar.
• Las muestras deben ser independientes.
• Las muestra deben ser continuas.
• Las muestras deber ser de distribución
  normal.

Debe acentuarse que el procedimiento para la t-test es
lo suficientemente veraz a las violaciones de la Asunción
de la normalidad, proveídas estas observaciones los datos
son recolectados al azar, son continuos, unimodal y
razonablemente sistemáticos. (ver Box, Hunter &
Hunter (1978). Statistics for Experimenters, John Wiley &
Sons, Inc.).