R. P. Feynman, premio Nóbel de física, dijo una vez
, "Ud. No sabe nada hasta que lo ha practicado". De acuerdo con
esta afirmación, reitero el consejo de que desarrolle las
habilidades necesarias para resolver una amplia gama de problemas. Su
capacidad para solucionarlos será una de las principales
pruebas de su
conocimiento
de física y, en consecuencia, debe tratar de resolver el
mayor número posible de problemas.
Es esencial que comprenda los conceptos y principios
básicos antes de intentar resolverlos. Una buena
práctica consiste en tratar de encontrar soluciones
alternas al mismo problema. Por ejemplo, los de mecánica pueden resolverse con las leyes de
Newton, aunque con frecuencia es mucho más directo un
método
alternativo que usa consideraciones de energía. No deben
detenerse en pensar entender el problema después de ver su
solución en clase. Debe
ser capaz de resolver el problema y problemas similares por si
solo.
El científico no estudia la naturaleza
porque sea útil; la estudia porque se deleita en ella, y
se deleita en ella porque es hermosa. Si la naturaleza no fuera
bella, no valdría la pena conocerla, y si no ameritara
saber de ella, no valdría la pena vivir la
vida.
Henri Poincare
LAS LEYES DEL
MOVIMIENTO
5.1 El concepto de
fuerza
5.2 Primera ley de newton y
marcos de referencia inerciales
5.3 Masa inercial
5.4 Segunda ley de Newton
5.5 Peso
5.6 La tercera ley de Newton
5.7 Algunas aplicaciones de las leyes de
Newton
Fuerzas de fricción
PROBLEMA DE REPASO DE LA FÍSICA DE SERWAY .
Pág. 132 de la cuarta edición.
Considere los tres bloques conectados que se muestran en
el diagrama.
Si el plano inclinado es sin fricción y el
sistema esta en
equilibrio,
determine (en función de
m, g y θ).
a) La masa M
b) Las tensiones T1 y
T2.
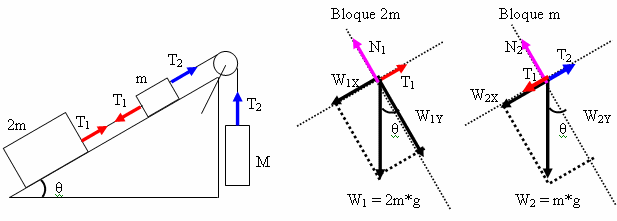
Bloque 2m
∑Fx = 0
T1 – W1X = 0
Pero: W1X = W1 sen
θ W1 = 2m*g
W1X = (2m*g) sen
θ
Reemplazando
T1 – W1X = 0
T1 – (2m*g) sen
θ = 0 (Ecuaciσn 1)
Bloque m
∑Fx = 0
T2 – T1 – W2X =
0
Pero: W2X = W2 sen
θ W2 = m*g
W2X = (m*g) sen
θ
Reemplazando
T2 – T1 – W2X =
0
T2 – T1 – (m*g)
sen θ = 0 (Ecuación
2)
Resolviendo las ecuaciones
tenemos:
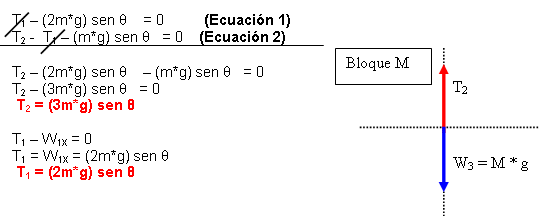
Bloque M
∑FY = 0
T2 – W3 = 0
T2 = W3
W3 = M * g
T2 = M * g
Pero: T2 = (3m*g) sen
θ
T2 = M * g
M * g = (3m*g) sen θ
a) La masa M
M = 3 m sen θ
Si se duplica el valor
encontrado para la masa suspendida en el inciso a),
determine:
c) La aceleración de cada
bloque.
d) Las tensiones T1 y
T2.
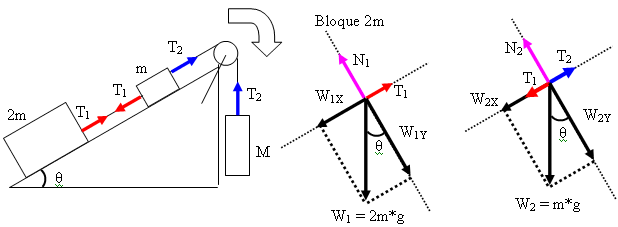
La masa es M = 3 m sen
θ
El problema dice que se duplique la masa
→ M = 2*(3 m sen
θ)
M = 6 m sen θ
Al duplicar la masa, el cuerpo se desplaza hacia la
derecha.
Bloque 2m
∑Fx = 2m * a
T1 – W1X = 2m * a
Pero: W1X = W1 sen
θ W1 = 2m*g
W1X = (2m*g) sen
θ
Reemplazando
T1 – W1X = 0
T1 – (2m*g) sen θ =
2m * a (Ecuaciσn 1)
Bloque m
∑Fx = m * a
T2 – T1 – W2X = m
* a
Pero: W2X = W2 sen
θ W2 = m*g
W2X = (m*g) sen
θ
Reemplazando
T2 – T1 – W2X = m
* a
T2 – T1 – (m*g) sen
θ = m * a (Ecuación 2)
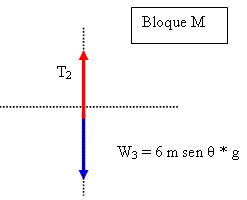
Bloque M
∑FY = 6 m sen θ
* a
W3 – T2 = 6 m sen
θ * a
W3 = 6 m sen θ
* g
6 m sen θ * g –
T2 = 6 m sen θ * a
(Ecuación 3)
Resolviendo las ecuaciones tenemos:
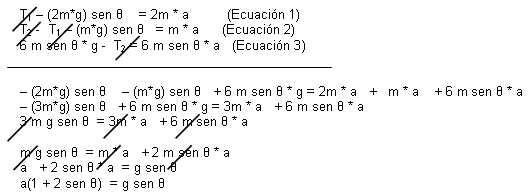
![]()
Despejando la ecuación 3 para hallar
T2
6 m sen θ * g –
T2 = 6 m sen θ * a
(Ecuación 3)
6 m sen θ * g – 6 m
sen θ * a =
T2
6 m sen θ ( g – a ) =
T2
Pero: ![]()
![]()
Factorizando g
![]()
![]()
![]()
![]()
Despejando la ecuación 1 para hallar
T1
T1 – (2m*g) sen θ =
2m * a (Ecuaciσn 1)
T1 = 2m * a + 2m*g sen
θ
Pero: ![]()
![]()
![]()
![]()
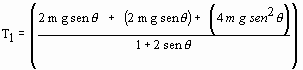
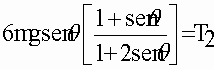
Factorizando
![]()
CAPITULO 5 LAS LEYES DEL
MOVIMIENTO
Problema 5.1 Edición quinta; Problema 5.1
Edición cuarta SERWAY
Una fuerza F
aplicada a un objeto de masa m1 produce una
aceleración de 3 m/seg2. La misma fuerza
aplicada a un objeto de masa m2 produce una
aceleración de 1 m/seg2 .
- Cual es el valor de la proporción
m1 / m2 - Si se combinan m1 y m2
encuentre su aceleración bajo la acción de F.
- Por la acción de la segunda ley de newton,
tenemos: a1 = 3 m/seg2
a2 =1 m/seg2
F = m1 * a1 (Ecuación
1)F = m2 * a2 (Ecuación
2)Como la fuerza F es igual para los dos objetos,
igualamos las ecuaciones.m1 * a1 = m2 *
a2

- Si se combinan m1 y m2
encuentre su aceleración bajo la acción de
F.
MT = m1 +
m2
F = (m1 + m2) * a
![]()
(Ecuación 3)
Pero: F = m1 * a1 =
m1 * 3
![]()
F = m2 * a2 = m2 *
1
![]()
Reemplazando m1 y m2 en la
ecuación 3, tenemos:
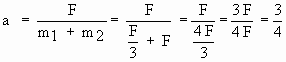
a = ¾ m/seg2
a = 0,75 m/seg2
Página siguiente  |
