Ampliación del contenido de integrales en cálculo (página 2)

Enviado por Miguel angel c Miguel angel c

Partes: 1, 2

Integral Indefinida

Dada una función
f(x), una primitiva arbitraria de f se denomina generalmente
integral indefinida de f(x) y se escribe en la forma.

La primitiva de una función también recibe
el nombre de antiderivada.

Si es
una función tal que para x en un intervalo , entonces la integral indefinida de
está dada
por:

C es cualquier número real y recibe el nombre de
constante de integración.

Puede decirse que si se conoce cualquier función
primitiva de de
la función , entonces cualquier otra primitiva de tiene la forma , donde C es una
constante.

PROPIEDADES DE LAS INTEGRALES
INDEFINIDAS

Si f(x) y g (x) son dos funciones que
tienen integral indefinida, y k es una constante,
entonces

La integral de la función nula f(x)=0,
es:

La integral de una función constante f(x)=k,
es:

Ejemplos:

La integral de una función f(x)=x, es

La integral de una función potencia f(x)=
, con , es:

Ejemplos:

MÉTODOS DE
INTEGRACIÓN

Los métodos de
integración son los medios por los
cuales se puede conocer una función indefinida que ya
está dada, pero que no conocemos, existen tres
métodos de integración, son uno es por el manejo de
la propiedades, otro es por sustitución y el ultimo es por
partes a su vez todos los métodos de integración
tienen por objetivo
transformar una integral dada, no inmediata, en otra, o suma de
varias, cuyo cálculo
resulte más sencillo.

.INTEGRACIÓN POR PARTES

La integración por partes consiste en descomponer
una integral en una suma de un producto de
funciones más una integral que, pretendidamente, es
más sencilla que la de partida.

El método de
integración por partes es el que resulta de aplicar el
siguiente teorema:

Eligiendo adecuadamente los valores de
u y dv, puede simplificarse mucho la
resolución de la integral.

Para elegir la función u se puede usar las
siguientes reglas:

Logarítmicas, Inversas, Algebraicas,
Trigonométricas, Exponenciales. LIATE.

Como norma general elegiremos como u la parte del
integrando fácil de derivar y como dv la parte
fácil de integrar. Sea la diferencial de la función
producto u·v:

DESARROLLO DEMOSTRACIÓN

Al integrar en ambos lados de la
ecuación:

Al cancelar derivada con la integral y separar la
integral de la suma en una suma de integrales se
obtiene:

Finalmente al despejar

Ejemplos:

u= x; dv=senx.dx. Entonces, du=dx
y v= -cosx.

INTEGRACIÓN POR
SUSTITUCIÓN

El método de integración por
sustitución se basa en realizar un reemplazo de
variables
adecuado que permita convertir el integrando en algo sencillo con
una integral
o antiderivada simple. En muchos casos, donde las
integrales no son triviales, se puede llevar a una

integral de tabla para encontrar
fácilmente su primitiva. Este método realiza lo
opuesto a la
regla de la cadena en la
derivación.

Esta integración esta definida por la
formula:

Ejemplos:

INTEGRAL DEFINIDA

Integral Definida: función del incremento del
área bajo la curva:

Imaginemos la representación gráfica de la
función y= f(x), donde se han trazado los segmentos
AoA1 y MM1 que definen la
superficie S de área A. Desplacemos el segmento en M una
distancia infinitesimal; supongamos que se mueve hasta el punto
N, desde donde levantamos el segmento NN1, como se
muestra en la
figura.

De esta manera la superficie S se incrementa en la
superficie definida por MM1N1N, que
denominaremos D S, cuya área la denotaremos con D A (se ha
exagerado el desplazamiento para lograr mayor
comprensión)
Si identificamos la abscisa del punto M con x y el incremento de
M a N con D x, al ser éste un infinitésimo podemos
considerar que el segmento M1N1 está
sobre una recta y puede aplicar la fórmula A=½ S
(rarb) d (rarb). Por
lo que:

D A =½(f(x) + f(x+D x)) D x, y dividiendo por D x
se tiende A =½(f(x) + f(x+D x)) Dx y al evaluar el
límite cuando D x tiende a cero:
Lim D A =Lim ½(f(x) + f(x+D x)) =½(2f(x)) =f(x) (D
x tiende a 0). D x
Luego, f(x) es la derivada del área; lo que nos indica que
el área es una función primitiva de f(x); la que
denotaremos con F(x).

Para determinar D A, bastará calcular f(x+D x) dx
– f(x) dx lo que se escribe: f(x) dx y que es igual a F(x+D x)-
F(x).

Integral Definida: sumatoria de incrementos de
áreas bajo la curva.

Supongamos ahora, la representación
gráfica de la función y=f(x), como se muestra en la
figura. Situemos dos puntos fijos a y b sobre los que
levantaremos rectas perpendiculares al eje x, de tal forma que
todo f(x) sea del mismo signo siempre que a<x<b.

De esta forma, hemos definido una figura cuya superficie
af(a)f(b)b se encuentra situada bajo la curva y=f(x) y limitada
por la recta x.
Tracemos un haz de rectas paralelas que contengan a las
levantadas, previamente, en los puntos a y b. Las distancias
entre rectas consecutivas pueden variar o pueden ser iguales;
pero, su cantidad será tal que las distancias entre dos de
ellas sea un infinitésimo. Con esto, la figura queda
dividida en superficies infinitamente pequeñas cuyas
áreas, en conjunto, suman el área de la figura que
las contiene.
Esta forma de dividir la figura es válida, tomando en
cuenta el criterio anteriormente utilizado para el cálculo
de incrementos de área bajo la curva, que nos
permitió establecer que f(x) y f(x+D x) se encuentran
situados en una misma recta (ver III). Cada recta del haz, junto
a la gráfica de la función y el eje x
contendrá un delimitador de las superficies infinitamente
pequeñas antes mencionadas.
Con estas premisas, podemos calcular el área bajo la curva
y= f(x) definida por los puntos a y b. Utilizando nuestra
fórmula para el área del polígono y
suponiendo k rectas paralelas del haz, identificadas desde a
hasta b como ri (i=0,…., k-1) tendremos:

A= å ½ S (riri+1) d
(riri+1), con I =0, k-2. Si identificamos
los puntos x donde se levanta cada recta, con el mismo
subíndice, tomando en cuenta que a=x0 y b=
xk-1, podemos calcular los incrementos de as
áreas a partir de ri así:

½ S (r0r1) d
(r0r1) = F(x1)-F(a)

½ S (r1r2) d
(r1r2) =
F(x2)-F(x1)

½ S (r2r3) d
(r2r3) =
F(x3)-F(x2)

½ S (r3r4) d
(r3r4) =
F(x4)-F(x3)

PROPIEDADES DE LAS INTEGRALES DEFINIDAS:

Propiedad 1: . Es decir, si la base del área de la
región najo la curva es cero, el área es
cero.

Propiedad 2: . Es decir, el área de la región bajo
la curva siempre será positiva si f(x) es
positiva.

Propiedad 3: . Es decir, que el área de la región
bajo la curva siempre será negativa si f(x) es
negativa.

Propiedad 4: si f es una función integrable en un
intervalo que contiene los puntos a, b y c, tal que
a<b<c,

Entonces:

Propiedad 5: Si f y g son funciones integrables en [a,
b], entonces también son f + g y f – g.
así:

Propiedad 6: , para toda k constante

Propiedad 7: , es decir, al intercambiar los limites de
integración cambia el signo de la integral.

Propiedad 8: si f y g son funciones integrables en [a,
b] y si ,
entonces .

Propiedad 9: , Es decir, si la función es constante, su
integral es el producto de las constante por la diferencia de los
limites de integración.

Ejemplo: Halle

Como f(x) = x3 es continua en el intervalo
[-2, 1] sabemos que es integrable.

Dividimos el intervalo en n subintervalos de igual
longitud y para el cálculo de la integral
consideramos el extremo   derecho   de
  cada   subintervalo
  ti =.

= =

Para el desarrollo de
la sumatoria tenemos en cuenta las propiedades
siguientes:

Observación: Esta integral definida es negativa,
no representa el área graficada. Las integrales definidas
pueden ser positivas, negativas o nulas.

APLICACIÓN DE LA INTEGRAL EN LOS
SÓLIDOS DE REVOLUCIÓN

Sea f una función definida en el intervalo
[a,b].

Recibe el nombre de sólido de
revolución, el sólido generado al girar
alrededor del eje x, la región limitada por la
gráfica de y= f(x), el eje x y las gráficas de x=a y x=b. El eje x es un eje
de simetría de dicho sólido y una sección
recta perpendicular al eje x es un círculo.

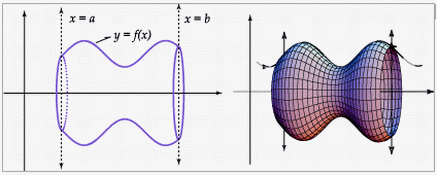
Para determinar el volumen de este
tipo de sólidos, seguiremos un procedimiento
similar al utilizado para el área de una región,
aproximando el "volumen" de un sólido de revolución
por medio de una suma de volúmenes de sólidos
más elementales, en los que el volumen ya ha sido
definido.

Vamos a considerar discos o cilindros circulares como
los sólidos elementales, suponiendo que el volumen de un
disco circular es, por definición, el producto del
área de la base por el espesor (o altura).

Consideremos una partición Pn del
intervalo [a,b.] determinada por el conjunto de
números

donde, con. , con

Sea un aumento de Pn.

Consideremos ahora los discos circulares, cuyos sensores
son , y cuyas bases tienen radios

El volumen del ésimo disco es:

La suma

de los volúmenes de los discos nos da una aproximación al
volumen del sólido de revolución.

Podemos suponer que mientras más delgados sean
los discos, mayor será la aproximación de la suma
anterior al volumen del sólido. Se tiene entonces la
siguiente definición:

Si existe un número tal que dada
exista para la cual

para toda partición Pn de [a,b] y todo
aumento Tn de Pn, y con , este número
es el volumen del sólido obtenido
por revolución del área limitada por las
gráficas de alrededor del eje x.

Si es la función dada por
para , entonces la suma de
aproximación:

utilizada en la definición del volumen del
sólido de revolución, puede escribirse
como:

donde .

Luego, de la definición de integral y de la
definición de dada, se tiene que

Consideremos ahora dos funciones f y g continuas
en el intervalo cerrado [a,b], tales que para . Sea la región del plano limitada por las
curvas con ecuaciones
y=f(x), y=g(x) y las rectas con ecuaciones x=a, x=b.

Deseamos determinar el volumen del sólido de revolución
generado al girar la región alrededor del eje x (note que en este caso
no giramos la región alrededor de una de sus
fronteras).

El sólido generado se muestra en la siguiente
figura:

Sea Pn una partición del intervalo
[a,b] determinada por el conjunto de números
con para , y
sea un aumento de Pn.

En este caso, los sólidos elementales usados para
obtener una suma de aproximación del volumen del
sólido de revolución, serán anillos
circulares.

Se muestra a continuación el ésimo rectángulo y el
ésimo anillo circular generado al
rotar aquel alrededor del eje .

Luego, el área del anillo circular es:

por lo que el volumen del ésimo elemento sólido
será:

Entonces, la suma de aproximación para el volumen del
sólido de revolución es:

Puede suponerse que mientras más delgados sean los anillos
circulares, mayor será la aproximación de la suma
anterior al volumen del sólido.

Si existe un número V tal que
dada exista para la cual

Para toda partición Pn de [a,b] y todo
aumento Tn de Pn, y con , este número de
es el volumen del sólido obtenido
por revolución del área limitada por las
gráficas de y=f(x), y=g(x), x=a, x=b, alrededor del eje
x.

Si h es la función dada por:
para , entonces la suma de
aproximación

Utilizada en la definición 8, puede
escribirse como:

donde .

Luego se tiene que:

CONCLUSIONES

La integral es una operación contraria a la
derivada, es decir, integral significa volver a la
función que se tenía antes de
derivar.
Para poder
integrar con éxito no solo es necesario aplicar bien
las propiedades de la derivación, sino también
saber usar los tres métodos de integración, el
de sustitución, integración por partes y
fracciones parciales.