Programa de electrotecnia II (página 2)

1.1.4.1 EL SPIN MAGNETICO

Una corriente
eléctrica genera un campo
magnético, y los electrones no apareados en los
átomos actúan como pequeños electroimanes
que apuntan en diversas direcciones, es decir, presentan polos
"norte" y "sur". Este comportamiento
está asociado al momento magnético
intrínseco o "spin" del electrón. Cuando los
spines de los electrones apuntan todos en la misma dirección en todos los átomos, el
material mismo actúa como un imán; el material se
llama ferromagnético, dado que el ejemplo
más simple es el hierro (figura
A). En realidad un trozo de hierro no es normalmente un
imán, sino que tiene que ser "magnetizado" mediante otro
imán. Esto se debe a que el material común consiste
de muchos pequeños cristalitos magnéticos cuyos
momentos magnéticos se cancelan entre sí porque
apuntan en direcciones al azar.

Si los spines o momentos magnéticos de los
átomos están en direcciones opuestas a escala
atómica, también se cancelan, y el material se
denomina antiferromagnético. El fluoruro de
manganeso (MnF, figura B) es un ejemplo simple. Los momentos de
los átomos de Mn en las esquinas del cubo apuntan en una
dirección, y los que se hallan en el centro del cubo
apuntan en la dirección opuesta. Dado que hay igual
número de cada uno, cuando muchas de estas celdas
unitarias se agrupan juntas, los momentos magnéticos se
cancelan exactamente.

1.2 LABORATORIO

El experimento siguiente es fundamental para mostrar que
solamente existen dos tipos de cargas.

1. Tomemos dos pequeñas esferas de un mismo
   cuerpo A (por ejemplo, vidrio frotado
   con un paño de seda), suspendámoslas como lo
   muestra la
   figura 1 y acerquémoslas. Notemos que se
   repelen.
2. El mismo experimento con otro cuerpo B (por ejemplo,
   ebonita frotada con piel), y
   suspendámoslas como lo muestra la figura 2. Notemos que
   se repelen.
3. El mismo experimento, pero una de las esferas es el
   cuerpo A(vidrio frotado) y la otra es el cuerpo B(ebonita
   frotada), suspendámoslas como muestra la figura .3.
   Notemos que se atraen.

En síntesis,
las cargas de un mismo nombre se repelen y las de nombres
distintos se atraen.

El concepto de carga
presenta algunas analogías con el concepto de masa. De
igual manera que todos los cuerpos o partículas tienen
asignados el atributo abstracto de masas, tiene también
una carga inherente que puede ser positiva, negativa o
nula.

1.3 LEYES
FUNDAMENTALES DEL MAGNETISMO.

Carga eléctrica

Como sabemos, la materia
está formada por átomos y éstos a su vez por
protones, neutrones y electrones.

Existe una fuerza llamada
electrostática que hace que un
electrón y un protón se atraigan entre sí
(fuerza de atracción) y dos electrones o dos protones se
repelan entre sí; (fuerza de repulsión).

Por lo tanto podemos decir que una carga
eléctrica es cualquier partícula capaz de crear
acciones
electromagnéticas (atracción o repulsión).
La unidad de carga eléctrica es el Culombio:

Ley de Coulomb

La fuerza entre cargas eléctricas es directamente
proporcional al producto de
dichas cargas e inversamente proporcional al cuadrado de la
distancia que las separa.

Si las cargas son de distinto signo, la fuerza
será; atractiva y si son del mismo signo la fuerza
será; repulsiva.

Donde: F = Fuerza de atracción o
repulsión en newtons

m1 = Masa magnética 1

m2 = Masa magnética 2

=
Permeabilidad del medio en que se encuentra.

d = Distancia de separación de las masas en
metros.

1.3.1 FUERZA MAGNETICA

Las fuerzas magnéticas son fuerzas de acción
a distancia, es decir, se producen sin que exista contacto
físico entre los dos imanes. Esta circunstancia, que
excitó la imaginación de los filósofos antiguos por su difícil
explicación, contribuyó más adelante al
desarrollo del
concepto de campo de fuerzas.

Cuando una carga q con una velocidad v
está en una región donde hay un campo
magnético, aparece una fuerza que depende de q y de v. A
esta fuerza se le llama fuerza magnética y viene definida
por la siguiente expresión:

Fm = q · v × B

donde B es el campo magnético.

Algunas características de la fuerza
magnética son:

– La fuerza magnética es proporcional a la carga
q.

– La fuerza magnética es proporcional al
módulo de la velocidad v.

– La fuerza magnética es perpendicular al plano
definido por los vectores de
campo magnético y velocidad.

– La fuerza magnética es proporcional al seno del
ángulo formado por los vectores de velocidad v y campo
magnético B. En el caso de que este ángulo fuera
cero, o sea que los dos vectores fueran paralelos, la fuerza
magnética sería nula.

En resumen, cuando una carga q se mueve con una
velocidad v en el interior de un campo magnético B,
actúa sobre ella la fuerza magnética Fm
.

La dirección y el sentido de la fuerza
magnética Fm vienen dados por la regla de la mano derecha,
girando de v hacia B.

1.3.2 UNIDADES MAGNETICAS MÁS
USUALES.

Dentro de las unidades magnéticas más
usuales tenemos que: La unidad en el Sistema
Internacional (S.I.) del campo magnético es la Tesla (T).
La fuerza hecha sobre una carga de 1 C que se mueve con una
velocidad de 1 m/s perpendicularmente a un campo magnético
de 1 T es de un Newton.

Como la Tesla es bastante grande se usa otra unidad que
es el Gauss (G) relacionada con el Tesla por:

1T = 104G

¡Ojo! Normalmente se utiliza el Gauss como unidad
del campo magnético, que no es una unidad SI, no debe
olvidarse la conversión de esta magnitud en Teslas cuando
se realizan los cálculos.

La unidad de carga eléctrica es el
Culombio:

1 C = 6 x 1018 e-

La carga del protón es: 1 p+ = 1.6019 x 10-19
C

La carga del electrón es: 1 e = -1.6019 x 10-19
C

La unidad SI del flujo magnético es el weber (Wb). Un
Weber es igual a 1 x 108 líneas de campo magnético.
Como el weber es grande para los campos comunes, se usa el
microweber (wb; 1 wb = 1 x
10-6).

1.3.3 CAMPO MAGNETICO

Campo magnético es la región del espacio
en la que se manifiestan los fenómenos magnéticos.
Estos actúan según unas imaginarias "líneas
de fuerza": éstas son el camino que sigue la fuerza
magnética. Se suele visualizar colocando un imán
bajo una cartulina espolvoreada con limaduras de hierro;
éstas se colocan siguiendo las líneas de
fuerza.

Se observa que hay una diferencia fundamental entre el
campo magnético y el eléctrico: en éste, el
campo nace en las cargas positivas y muere en las negativas. En
aquél, por el contrario no existen ni fuentes ni
sumideros: se cierra sobre sí mismo.

Decimos que existe un campo magnético en un punto
si sobre una carga q móvil que pasa por ese punto se
ejerce una fuerza perpendicular a la velocidad de la carga
(además de las fuerzas gravitacionales y
eléctricas).

Si la dirección de la velocidad de la carga
cambia, se observa que la fuerza es siempre perpendicular a la
velocidad y que su magnitud varía. Para una determinada
dirección de la velocidad, la fuerza se anula: se define
esta dirección como la dirección del campo
magnético, sin precisar aun su sentido.

Cuando la velocidad de la carga q es perpendicular a la
dirección anterior, la fuerza es máxima y
proporcional a v y a q.

Como se dijo anteriormente la unidad en el SI del campo
magnético es la Tesla (T).

LAS FUENTES DEL CAMPO
MAGNÉTICO.

Las primeras fuentes de campo magnético conocidas
fueron los imanes permanentes. Los campos magnéticos
formados por los imanes permanentes están entre 0.1 y 0.5
T.

En 1600, William Gilbert descubrió que la Tierra era
un imán natural con polos magnéticos cerca de los
polos geográficos. El campo magnético de la
Tierra es de
unos 10-4 T.

Otra fuente de campo magnético es el
electroimán. Los electroimanes más potentes pueden
llegar a producir campos magnéticos de hasta 2
T.

EL TRABAJO
REALIZADO:

La fuerza ejercida por un campo magnético sobre
una partícula cargada en movimiento es
siempre perpendicular a su velocidad, por lo tanto el trabajo
realizado por esta fuerza es siempre cero.

1.3.4 FLUJO MAGNETICO

La representación de la influencia
magnética de un imán o de una corriente
eléctrica en el espacio que les rodea mediante
líneas de fuerza fue ideada por Faraday, La noción
de flujo magnético recoge esa tradición iniciada
por el de representar los campos mediante líneas de
fuerza, pero añade, además, un significado
matemático.

Cuando se observa, con la ayuda de limaduras de hierro,
el campo magnético creado por un imán recto, se
aprecia que, en los polos, las líneas de fuerza
están más próximas y que se separan al
alejarse de ellos. Dado que la intensidad del campo
magnético B disminuye con la distancia a los polos, parece
razonable relacionar ambos hechos y establecer por convenio una
proporcionalidad directa entre la intensidad del campo B y la
cantidad de líneas de fuerza que atraviesan una superficie
de referencia unidad. Cuanto más apretadas están
las líneas en una región, tanto más intenso
es el campo en dicha región.

Se define el flujo del campo magnético B a
través de una superficie, y se representa por la letra
griega , como el número total de líneas de
fuerza que atraviesan tal superficie.

La idea de flujo se corresponde entonces con la de
«cantidad» de campo magnético que atraviesa
una superficie determinada. En el Sistema Internacional se
expresa en wéber (Wb).

Ejemplo: Si un flujo magnético  tiene
3000 líneas, encuéntrese el número de
microwebers.

Conviértase el número de líneas en
microwebers.

DENSIDAD DEL FLUJO MAGNETICO

La
densidad del
flujo magnético es el flujo magnético por unidad de
área de una sección perpendicular a la
dirección del flujo. La ecuación de la densidad de
flujo magnético es:

En la cual: B = densidad de flujo magnético en
teslas (T)

 = flujo magnético en Wb

A = área en metros cuadrados (m2)

Vemos que la unidad SI de B es el weber por metro
cuadrado (Wb x m2). Un weber por metro cuadrado se llama una
tesla.

Ejemplo:
¿Cual es la densidad de flujo en teslas cuando existe un
flujo de 600  Wb por un área de 0.0003
m2?

Sustitúyanse
los valores de
 y de A en la ecuación de flujo
magnético.

2.
ELECTROMAGNETISMO

En 1819 el científico danés Oersted
descubrió una relación entre el magnetismo y la
corriente eléctrica. Encontró que una corriente
eléctrica que circula por un conductor produce un campo
magnético alrededor de éste.

2.1 CAMPO ALREDEDOR DE UN CONDUCTOR RECORRIDO POR UNA
CORRIENTE.

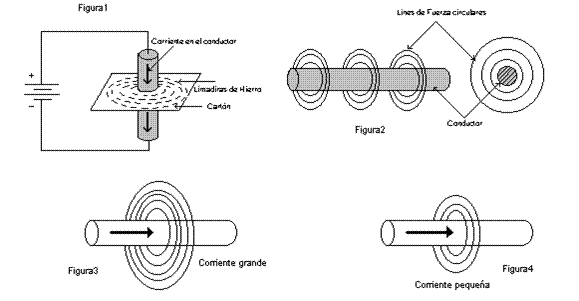
Teniendo en cuenta la figura1 donde tenemos un conductor
atravesado por una corriente, las líneas de fuerza
representadas por las limaduras forman anillos
concéntricos alrededor del conductor, revelan la presencia
del campo magnético de la corriente en el alambre. Cada
sección del alambre tiene en su alrededor este campo de
fuerza en un plano perpendicular al alambre figura2. La
intensidad del campo magnético en el alambre alrededor de
un conductor depende de la corriente que pasa por éste.
Una corriente grande producirá muchas líneas de
fuerza que se extenderán hasta cierta distancia del
alambre figura3, mientras que una corriente pequeña
producirá solo unas cuantas líneas cerca del
alambre figura4.

2.2 CAMPO SOLENOIDE RECORRIDO POR UNA
CORRIENTE.

Si a un conductor recto se le dobla dándole la
forma de espira, se producen dos efectos. Primero, las
líneas del campo magnético son más densas
dentro de la espira, aunque el número total de
líneas es el mismo que para el conductor recto. Segundo,
todas las líneas en el interior de la bobina se suman por
tener la misma dirección.

Un solenoide es, en esencia, un conjunto de espiras
iguales y paralelas dispuestas a lo largo de una determinada
longitud que son recorridas por la misma intensidad de corriente.
Su forma es semejante a la del alambre espiral de un bloc. El
espectro magnético del campo creado por un solenoide se
parece más aún al de un imán recto que el
debido a una sola espira. La regla que permite relacionar la
polaridad magnética del solenoide como imán con el
sentido convencional de la corriente que circula por él es
la misma que la aplicada en el caso de una sola
espira.

El
estudio experimental de la intensidad del campo magnético
B debido a un solenoide en un punto cualquiera de su interior
pone de manifiesto que una mayor proximidad entre las espiras
produce un campo magnético más intenso, lo cual se
refleja en la expresión de B a través del cociente
N/L, siendo N el número de espiras y L la longitud del
solenoide. Dicha expresión viene dada por la
ecuación:

N/L representa el número de espiras por unidad de
longitud.

Siendo su valor tanto
mayor cuanto más apretadas están las espiras en el
solenoide. El hecho de que B dependa del valor de , y por
tanto de las características del medio, sugiere la
posibilidad de introducir en el interior del solenoide una barra
de material de elevado y conseguir así un campo
magnético más intenso con la misma intensidad de
corriente I. Este es precisamente el fundamento del
electroimán, en el cual una barra de hierro introducida en
el hueco del solenoide aumenta la intensidad del campo
magnético varios miles de veces con respecto al valor que
tendría en ausencia de tal material. Los timbres, los
teléfonos, las dinamos y muchos otros dispositivos
eléctricos y electromecánicos utilizan
electroimanes como componentes. Sus características de
imanes temporales, que actúan sólo en presencia de
corriente, amplía el número de sus posibles
aplicaciones.

2.3 POLARIDAD DE UN ELECTROIMAN

Como sabemos una bobina de alambre conductor se forma si
hay de una espira o vuelta. Para determinar la polaridad
magnética de una bobina, se usa la regla de la mano
derecha. Si la bobina se toma con la mano derecha y los dedos se
doblan en la dirección en la que circula la corriente en
la bobina, el pulgar apunta al polo norte de
esta.

La inserción de un núcleo de hierro en el
interior de la bobina aumenta la densidad de flujo. La polaridad
del núcleo es la misma que la de la bobina. La polaridad
depende de la dirección del flujo de la corriente y de la
dirección del devanado o arrollado. El flujo de la
corriente va del lado positivo de la fuente de voltaje, pasando
por la bobina, hasta la terminal negativa de la fuente. El polo
norte se identifica también con la regla de la mano
derecha.

2.4 FUERZA DE UN ELECTROIMAN

Se dice que un electroimán es un imán
temporal constituido por una bobina cilíndrica de alambre
arrollada en forma de espiral(solenoide), en cuyo interior se
coloca un núcleo de hierro. Cuando una corriente
eléctrica recorre la bobina, se crea un fuerte campo
magnético, paralelo a su eje. En el núcleo, las
partículas de hierro, que pueden considerarse
pequeños imanes permanentes, se alinean en la
dirección del campo, aumentando notablemente la fuerza del
campo magnético generado por el solenoide. El
núcleo se satura cuando todas las moléculas
están alineadas, por lo que a partir de entonces el
aumento de la corriente no incremente la fuerza del campo
magnético. Si se interrumpe la corriente, las
moléculas se redistribuyen y sólo se mantiene un
débil magnetismo residual.

Los electroimanes son componentes fundamentales de los
circuitos
automáticos y manuales de
mando, y como frenos y embragues electromagnéticos. En los
aceleradores de partículas se utilizan enormes
electroimanes con núcleos de varios metros de
diámetro, también se utilizan potentes
electroimanes como grúas, para levantar hierro y chatarra
en las plantas de
recuperación y fundiciones.

2.5 FUERZA ELECTROMAGNETICA

Cuando las cargas eléctricas están en
movimiento, como por ejemplo los electrones a través de un
alambre de cobre, generan
una fuerza llamada magnetismo. Magnetismo y electricidad son
complementarios, por eso se habla de fuerza
electromagnética. Existiendo cargas en movimiento
(corriente eléctrica), se producirá magnetismo. Y,
si tenemos una fuerza magnética variable, se
producirá corriente eléctrica.

La fuerza electromagnética ve a las fuerzas
eléctricas, descritas por Coulomb, y magnéticas,
descritas por Ampère y Faraday, como dos aspectos del
mismo fenómeno en una teoría
desarrollada en los años 1860 por James C. Maxwell.
Solamente partículas con carga eléctrica y el
fotón están sujetas a esta interacción. Como sabemos la fuerza puede
ser de atracción (entre cargas de signos
opuestos) o de repulsión (cargas iguales). Esta fuerza es
responsable de la cohesión del átomo y
las moléculas. Además mantiene los objetos
cotidianos como entidades con forma propia. Un vaso, una piedra,
un auto, el cuerpo humano.
Es mucho más fuerte que la gravitación y aunque es
de alcance infinito, las cargas de distinto signo se compensan y
sus efectos no operan a grandes distancias. Dependiendo de las
circunstancias en que actúen, estas interacciones pueden
manifestarse como fuerzas eléctricas o magnéticas
solamente, o como una mezcla de ambos tipos. Por ejemplo, la
partícula portadora de la fuerza electromagnética
es el fotón, de masa nula y, por lo tanto, alcance
infinito.

Estrictamente hablando, no hay campos
"electromagnéticos", sino, en cambio, existe
un efecto de fuerza electromagnética que es la suma de
fuerzas de los campos eléctricos y magnéticos. Los
efectos físicos de esas fuerzas electromagnéticas
son principalmente la ionización de la atmósfera y la
atracción de radón en su área de
influencia.

2.6 LEYES FUNDAMENTALES DEL
ELECTROMAGNETISMO

2.6.1 TEOREMA DE AMPERE

Un experimento simple realizado por Oesterd en 1820
demostró claramente el hecho de que un conductor que lleva
una corriente produce un campo magnético. En este
experimento varias brújulas se colocan en un plano
horizontal cercanas a un alambre largo vertical como lo muestra
la figura 1. Cuando no existe corriente en el alambre, todas las
brújulas apuntan en la misma dirección (que el
campo terrestre) como se esperaría. Sin embargo, cuando el
alambre lleva una gran corriente estable, las brújulas
necesariamente se desviarán en la dirección
tangente a un círculo como lo muestra la figura 2.
Deduciendo que si se toma el alambre con la mano derecha, de tal
forma que el dedo pulgar apunte en la dirección de la
corriente, los dedos curvados definirán la
dirección de B.

Cuando la corriente se invierte, necesariamente las
brújulas de la figura 2 se invertirán
también. Puesto que las brújulas apuntan en la
dirección de B, se concluye que las líneas de B
forman círculos alrededor del alambre. Si se varía
la corriente y la distancia al alambre, se encuentra que B es
proporcional a la corriente e inversamente proporcional a la
distancia al alambre.

2.6.2 LEY DE BIOT
SAVART

Poco tiempo
después del descubrimiento de Oersted en 1819, donde la
aguja de la brújula se
desviaba a causa de la presencia de un conductor portador de
corriente, Jean Baptiste Biot y Felix Savart informaron que un
conductor de corriente estable produce fuerzas sobre un
imán. De sus resultados experimentales, Biot y Savart
fueron capaces de llegar a una expresión de la que se
obtiene el campo magnético en un punto dado del espacio en
términos de la corriente que produce el campo. La ley de
Biot Savart establece que si un alambre conduce una corriente
constante I, el campo magnético dB en un punto P debido a
un elemento ds(figura) tiene las siguientes
propiedades:

1. El vector dB es perpendicular tanto a ds(el cual
   tiene la dirección de la corriente)como el vector
   unitario r’ dirigido desde el elemento hasta el punto
   P.
2. La magnitud dB es inversamente proporcional a r2,
   donde r es la distancia desde el elemento hasta el punto
   P.
3. La magnitud de dB es proporcional a la corriente y la
   longitud ds del elemento.
4. La magnitud de dB es proporcional a sen q , donde q es el
   ángulo entre el vector ds y r’.

La
Ley de Biot Savart puede ser resumida en la siguiente
forma:

2.7 PERMEABILIDAD MAGNETICA

La permeabilidad se refiere a la capacidad que tiene un
material magnético de concentrar el flujo
magnético. Cualquier material que se magnetice
fácilmente tiene una permeabilidad elevada. La medida de
la permeabilidad de los materiales con
referencia a la del aire o a la del
vació se llama permeabilidad relativa. El
símbolo de la permeabilidad relativa es el r (mu),
en el que el subíndice r indica relativa. r, no
tiene unidades porque es el cociente de dos densidades de flujo,
así las unidades se cancelan.

La clasificación de los materiales como
magnéticos o no-magnéticos se basa en las intensas
propiedades magnéticas del hierro. Sin embargo, como los
materiales débilmente magnéticos pueden tener
importancia en algunas aplicaciones, la clasificación
incluye tres grupos:

1. Materiales ferromagnéticos. Estos
   incluyen al hierro, acero,
   níquel, cobalto y aleaciones
   comerciales como el alnico y permalloy. Las ferritas son
   materiales no magnéticos que tienen las mismas
   propiedades ferromagnéticas que el hierro. Una ferrita
   es un material cerámico. La permeabilidad de las
   ferritas se encuentra en la región de 50 a 3000. Una
   aplicación de común de las ferritas es su
   empleo como
   núcleos en el centro de los devanados de los transformadores
   de radiofrecuencia (RF).
2. Materiales paramagnéticos. En estos se
   incluyen el aluminio,
   platino, manganeso, y cromo. Su permeabilidad relativa es
   ligeramente mayor que 1.
3. Materiales diamagnéticos. En estos se
   encuentran el bismuto, antimonio, cobre, zinc, mercurio,
   oro y plata.
   

En 1948, Taggart estableció una
clasificación de los minerales
basándose en su permeabilidad magnética relativa al
hierro, el cual se considera como la sustancia más
magnética, como se muestra en la siguiente
tabla:

2.8 UNIDADES

Ampere-vueltas NI

La intensidad del campo magnético en una bobina
de alambre arrollado depende de la cantidad de corriente que
fluya por las vueltas de la bobina. Mientras mayor sea la
corriente, mas intenso será el campo magnético. De
igual manera, cuantas mas vueltas haya, mas concentradas
serán las líneas de fuerza. El producto de la
corriente por el número de vueltas de la bobina, que se
expresa en ampere-vueltas (At), se conoce como fuerza
magnetomotriz (fmm). En fórmula,

F = ampere-vueltas= NI

En la cual F = fuerza magnetomotriz en
At

N = número de vueltas

I = corriente en A

Ejemplo:
Calcúlese la el número de ampere-vueltas para una
bobina con 1500 vueltas y una corriente de 4mA.

2.9 INTENSIDAD DEL CAMPO MAGNETICO
H

Si una
bobina con un número fijo de ampere-vueltas se estira al
doble de su longitud original, la intensidad del campo
magnético (es decir, la concentración de las
líneas de fuerza) se reducía a la mitad del valor
original. Por lo tanto, la intensidad del campo depende de la
longitud de la bobina. Expresado en forma de
ecuación,

En la que H = intensidad del campo magnético
en ampere-vueltas por metro (At/m)

NI = ampere-vueltas (At)

l = longitud o distancia entre los polos de la bobina
en m

Esta ecuación se aplica a un solenoide. H es la
intensidad en el centro de un núcleo de aire. Con un
núcleo de hierro, H es la intensidad en todo el
núcleo y l es la longitud o distancia entre los polos del
núcleo de hierro.

2.10
FOTORRESISTENCIAS.(HISTERESIS)

Cuando un material ferromagnético, sobre el cual
ha estado
actuando un campo magnético, cesa la aplicación de
éste, el material no anula completamente su magnetismo,
sino que permanece un cierto magnetismo residual.

Para desimantarlo será precisa la
aplicación de un campo contrario al inicial. Este
fenómeno se llama HISTERESIS magnética, que
quiere decir, inercia o retardo. Los materiales tiene una cierta
inercia a cambiar su campo magnético.

La figura representa el llamado CICLO DE
HISTERESIS (también lazo o bucle de
histéresis) de un determinado material magnético.
Se supone que una bobina crea sobre dicho material
magnético una intensidad de campo H, el cual induce en ese
material magnético una inducción (valga la redundancia) de valor
B. Así a una intensidad de campo H0 le
corresponderá una inducción de valor B0. Si ahora
aumenta H (aumentando la corriente que circula por la bobina)
hasta un valor H1, B también aumentará hasta B1.
(Ver figura) Pero si ahora restituimos H a su valor inicial H0 ,
B no vuelve a B0 , sino que toma un valor diferente B2.
(Obsérvese que el camino "a la ida" es distinto que "a la
vuelta" lo que implica que para restituir la inducción en
el núcleo a su primitivo valor, es preciso aplicar una
corriente suplementaria de signo opuesto). El punto S representa
la saturación del núcleo magnético. Una vez
saturado el núcleo, B no puede aumentar por mucho que lo
haga H. Cada material tiene su propio lazo de histéresis
característico. Hay veces en que interesa acentuar la
histéresis, como ocurre en los núcleos de las
memorias
magnéticas, por lo que se fabrican ferritas con doble
ciclo como el de la figura siguiente:

Otras veces por el contrario, como ocurre en la
mayoría de las máquinas
eléctricas (transformadores, motores,
generadores), interesa un núcleo cuyo ciclo de
histéresis sea lo más estrecho posible ( el camino
"a la ida" coincida con el camino "a la vuelta") y lo más
alargado posible (difícilmente saturable), como el de la
figura siguiente:

2.11 RELUCTANCIA

El símbolo de la reluctancia es R .La reluctancia
es inversamente proporcional a la permeabilidad. El hierro tiene
una permeabilidad alta y por lo tanto una reluctancia baja. El
aire tiene poca permeabilidad y por ende alta
reluctancia.

Las distintas formas de los electroimanes tienen
diferentes valores de
reluctancia como lo muestra la siguiente figura. El entrehierro
es el espacio de aire entre los polos de un electroimán.
Como el aire tiene una reluctancia grande, el tamaño del
entrehierro afecta al valor de la reluctancia. El circuito de la
figura A tiene los polos muy separados en el aire, por lo cual
tiene una elevada reluctancia. En la figura B la reluctancia ha
disminuido acercando los polos. El campo entre N y S es
más intenso, suponiendo el mismo número de
ampere-vueltas en las bobinas. En la figura C el entrehierro es
menor que en la figura B, así que la reluctancia es menor.
En la figura D no hay entrehierro en el núcleo toroidal,
así que su reluctancia es extremadamente
pequeña.

Cuanto más pequeño sea el entrehierro,
más intenso será el campo en esa región.
Como el aire no es magnético y por consiguiente, es
incapaz de concentrar las líneas magnéticas, un
entrehierro más amplio solo proporcionará mas
espacio para que las líneas magnéticas se
dispersen.

2.12 CIRCUITOS MAGNETICOS

Un circuito magnético puede compararse con una
corriente eléctrica en la que una f.e.m produce un flujo
de electrones. Considérese un circuito magnético
sencillo figura 1. El número de ampere-vueltas NI de la
fuerza magnetomotriz produce el flujo magnético
 Por consiguiente, la fmm se compara con
la fem o el voltaje y el flujo  se compara con la
corriente. La oposición a la producción de flujo en un material se llama
reluctancia, que corresponde a la resistencia
eléctrica.

Ley de Ohm de los circuitos
magnéticos.

La ley de Ohm de los
circuitos magnéticos, correspondiente a I = V/R,
es:

en la que 
flujo magnético en Wb

fmm = fuerza magnetomotriz en At

R = reluctancia en At/Wb

La reluctancia puede expresarse con una ecuación
como se indica:

en la cual R = reluctancia en
At/Wb

l = longitud de la bobina en m

= permeabilidad del
material magnético en (T x m)/At

A = área de la sección transversal
de la bobina en m2

Ejemplo.

Una bobina tiene una fmm de 500 At y una reluctacia de 2
x 108 At/Wb. Calcúlese el flujo total 
Escríbase la ley de Ohm de los circuitos magnéticos
y sustitúyanse los valores conocidos.

3.
FUERZA ELECTROMOTRIZ INDUCIDA

3.1 INDUCCION ELECTROMAGNÉTICA DEBIDO AL CORTE
DE UN CAMPO MAGNETICO

En 1831 Michael Faraday descubrió el principio de
la inducción electromagnética, el cual afirma que
si un conductor "corta" líneas de fuerza o que si las
líneas de fuerza cortan un conductor, se induce una Fem. o
un voltaje entre los extremos del conductor. Considérese
un imán con sus líneas de fuerza que se extienden
del polo norte al polo sur, como lo muestra la figura. Un
conductor C que puede moverse entre los polos del imán,
esta conectado a un galvanómetro G utilizado para indicar
la existencia de una fem. Cuando el conductor no se mueve, el
galvanómetro indica cero fem. Si el alambre conductor se
mueve fuera del campo magnético en la posición 1,
el galvanómetro seguirá con indicación cero.
Cuando el conductor se mueve hacia la izquierda a la
posición 2, corte las líneas de fuerza
magnéticas y la aguja del galvanómetro se
deflectarà hacia A. Esto indica que en el conductor se
indujo una fem al cortarse las líneas de fuerza. En la
posición 3, la aguja del galvanómetro regresa a
cero porque no se cortan las líneas de fuerza.
Inviértase ahora la dirección de movimiento del
conductor moviéndolo por las líneas de fuerza de
regreso a la posición 1. Durante este movimiento, la aguja
se desviará hacia B, lo cual indica que se indujo una fem
en el alambre pero en la dirección opuesta. Si el alambre
se mantiene estacionario en el centro del campo de fuerza en la
posición 2, el galvanómetro indica cero. Si el
conductor se mueve hacia arriba o hacia abajo, paralelo a las
líneas de fuerza de manera que no corte ninguna, no se
inducirá ninguna fem.

En resumen:

1. Cuando un conductor corta líneas de fuerza o
las líneas de fuerza cortan un conductor, se induce en el
conductor una F.e.m o voltaje.

2. Para que se induzca una F.e.m, debe haber movimiento
relativo entre el conductor y las líneas de
fuerza.

3. Al cambiar la dirección en la que se cortan
las líneas o el conductor, también cambia la
dirección de la F.e.m Inducida.

3.1.1 EXPERIMENTO DE FARADAY

LEY DE FARADAY DEL VOLTAJE INDUCIDO

El valor del voltaje inducido depende del número
de vueltas de una bobina y la rapidez con la que el conductor
corta las líneas de fuerza o el flujo magnético;
puede moverse el conductor o el flujo.

La ecuación con la que podemos calcular el valor
del voltaje inducido es:

en la cual:

Vind = voltaje inducido en V

N = número de vueltas en la
bobina


= rapidez con la que el flujo corta el conductor en
Wb/s

3.2 FACTORES QUE DETERMINAN LA FUERZA ELECTROMOTRIZ
INDUCIDA.

A partir de la anterior ecuación deducimos que el
Voltaje inducido está determinado por tres
factores:

1. La cantidad de flujo: Cuanto mas líneas
   de flujo corten al conductor, mayor será el valor del
   voltaje inducido.
2. Número de vueltas: Mientras más
   vueltas tenga la bobina, mayor será el voltaje
   inducido.
3. Rapidez con la que se corten las
   líneas: Cuanto mas rápido corte el flujo a un
   conductor o el conductor corte al flujo, mayor será el
   voltaje inducido porque habrá mas líneas de
   fuerza que corten al conductor en cierto intervalo.

3.2.1 PRINCIPIO BASICO DEL ALTERNADOR.

Un voltaje de ca cambia continuamente en magnitud y
periódicamente invierte su polaridad. El eje del cero es
una línea horizontal que pasa por el centro. Las
variaciones verticales de la onda de voltaje muestran los cambios
en su magnitud. Los voltajes por arriba del eje horizontal tienen
polaridad positiva (+), mientras que los voltajes por abajo del
eje tienen polaridad negativa (-).

Un voltaje de corriente alterna
puede ser producido por un generador llamado alternador como lo
muestra la figura anterior. En el generador simplificado que se
muestra, la espira conductora gira en el campo magnético y
corta las líneas de fuerza para generar un voltaje
inducido de ac entre sus terminales. Una revolución
completa de la espira es un ciclo. Considérese la
posición de la espira e cada cuarto de vuelta durante un
ciclo como lo muestra la siguiente figura. En la posición
A, la espira se mueve paralela al flujo magnético y por
consiguiente no corta las líneas de fuerza; el voltaje
inducido es cero. En la posición B de la parte superior
del círculo, la espira corta el campo a 90º para
producir un voltaje máximo. Cuando llega a C, el conductor
se mueve otra vez paralelo al campo y no corta al flujo. La onda
de ac desde A hasta C es medio ciclo de la revolución y se
llama alternación. En D la espira corta otra vez al
flujo para producir voltaje máximo, pero ahora el flujo se
corta en dirección opuesta (de izquierda a derecha) que en
B (de derecha a izquierda); por consiguiente, la polaridad en D
es negativa. La espira completa la última cuarta parte de
la vuelta en el ciclo al regresar a la posición A, el
punto de partida. El ciclo de los valores del voltaje se repite
en las posiciones A,B,C,D,A al continuar girando la
espira.

3.2.2 PRINCIPIO BASICO DE UN MOTOR DE
CC.

Aunque la construcción mecánica de los motores y los generadores
de cc es muy similar, sus funciones son muy
diferente. La función de
un generador es generar voltaje cuando se mueven conductores en
un campo, mientras que la de un motor es producir fuerza
giratoria, llamada par motor que produce rotación mecánica.

Dirección de rotación de la
armadura

Para determinar la dirección de rotación
de los conductores de la armadura se usa la regla de la mano
izquierda. La regla de la mano izquierda para los motores es la
siguiente: colóquese los dedos índice, medio y
pulgar mutuamente perpendiculares, apúntense con el
índice en la dirección del campo y con el dedo
medio en la dirección de la corriente en el conductor; el
pulgar apuntara en la dirección en la que el conductor
trata de moverse figura A. En una bobina rectangular de una sola
espira colocada paralela a un campo magnético figura B, la
dirección de la corriente en el conductor de la izquierda
es hacia fuera del papel, mientras que en el conductor de la
derecha es hacia adentro del papel; por consiguiente el conductor
de la izquierda tiende a moverse hacia arriba con una fuerza F1 y
el conductor de la derecha tiende a moverse hacia abajo con una
fuerza igual F2. Ambas fuerzas actúan ejerciendo un par
que hace girar a la bobina en el sentido de las manecillas del
reloj. Un motor con una sola bobina es impractico por tener
puntos muertos y porque el par ejercido es pulsante. Se obtienen
buenos resultados al usar un número grande de bobinas,
como en un motor de cuatro polos. Al girar la armadura y alejarse
los conductores de un polo hacia el plano neutro. La corriente se
invierte por la acción del conmutador. De esta manera, los
conductores bajo un polo dado llevan corriente en la misma
dirección todo el tiempo.

3.2.3 PRINCIPIO BASICO DEL GENERADOR DE
CC.

Un generador es una máquina que convierte la
energía mecánica giratoria en energía
eléctrica. La energía mecánica puede ser
proporcionada por una caída de agua, vapor,
viento o por un motor de gasolina, diesel o
eléctrico.

El generador simplificado de cc consiste de una bobina
de armadura con una espira de alambre. La bobina corta al campo
magnético para producir voltaje. Si se tiene una
trayectoria completa (circuito cerrado), la corriente circulara
por el circuito en la dirección indicada por la flechas
figura A. En esta posición de la bobina, el segmento 1 del
conmutador hace contacto con la escobilla 1, mientras que el
segmento 2 del conmutador está en contacto con la
escobilla 2. Cuando la armadura gira media vuelta en sentido de
las manecillas del reloj, se invierten los contactos entre los
segmentos del conmutador y las escobillas figura B. En ese
momento el segmento 1 hace contacto con la escobilla 2 y el
segmento 2 hace contacto con la escobilla 1. Debido a la
acción del conmutador, el lado de la bobina de la armadura
que esta en contacto con cualquiera de las dos escobillas siempre
corta al campo magnético en la misma dirección. Por
consiguiente, las escobillas 1 y 2 siempre tienen la misma
polaridad y al circuito externo de carga se le entrega una
corriente continua pulsante.

4.
TENSIONES E INTENSIDAD VARIABLES EN
FUNCION DEL TIEMPO

4.1 ONDAS
SENOIDALES

La forma de onda del voltaje (Fig 11-3)se llama onda
senoidal. El valor instantáneo del voltaje en cualquier
punto de la onda senoidal se expresa por la
ecuación

v = VM sen 

4.1.1 FRECUENCIA

El número de ciclos por segundo se llama
frecuencia, se indica con la letra f y se expresa en hertz
(Hz). Un ciclo por segundo es igual a un hertz. Por lo tanto, 60
ciclos por segundo (abreviado a veces cps) es igual a 60 Hz. Una
frecuencia de 2 Hz (Fig. 11-7b) es el doble de la frecuencia de 1
Hz (Fig 11-a).

4.1.2 PERIODO

El tiempo que se requiere para completar un ciclo se
llama periodo. Se indica por el símbolo T (por tiempo) y
se expresa en segundos (s). La frecuencia y el periodo son
recíprocos.

Cuanto mayor sea la frecuencia, menor será el
periodo.

El ángulo de 360º representa el tiempo de 1
ciclo, o sea, el periodo T. Por lo tanto, podemos indicar en el
eje horizontal de la onda senoidal unidades de grados
eléctricos o de segundos.

4.2 AMPLITUD MÁXIMA DE LA CA.

Se le llama amplitud máxima o valor pico al valor
máximo VM o IM. Se aplica tanto al pico positivo como al
negativo. Se puede especificar el valor pico a pico (p-p), que es
el doble del valor pico cuando los picos positivos y los
negativos son simétricos.

4.3 AMPLITUD MEDIA DE LA CA.

El valor promedio es el promedio aritmético de
todos los valores de una onda senoidal durante medio ciclo. El
medio ciclo se utiliza para obtener el promedio porque el valor
promedio durante un ciclo completo es cero.

4.3 VALOR CUADRÁTICO.

La raíz cuadrática media (rms) o valor
efectivo es 0.707 veces el valor pico. El valor rms de una onda
senoidal alterna corresponde a la misma cantidad de corriente o
voltaje continuos en potencia de
calentamiento. Por ejemplo, un voltaje alterno con un valor rms
de 115V es igualmente efectivo para calentar el filamento de un
foco de 115V de una fuente estacionaria o estable de voltaje de
cc. Por esta razón, el valor rms se llama también
el valor efectivo.

A menos que se indique lo contrario, todas las
mediciones de ondas de ac senoidales están dadas en valor
rms. Las letras V e I se usan para indicar el voltaje y la
corriente rms. Por ejemplo, V=220V (un voltaje de línea de
alimentación de ca) se entiende que
significa 220V rms.

4.4 VALOR INSTANTANEO Y ECUACION
MATEMATICA

La forma de onda del voltaje (Fig. 11-3) se llama onda
senoidal. El valor instantáneo del voltaje en cualquier
punto de la onda senoidal se expresa por la
ecuación:

v =VM sen 

en donde v = valor instantáneo del voltaje
en V

VM = valor máximo

 = Angulo de rotación en
grados.

4.5 TALLER DE EJERCICIOS

Autor:

WULKAN