En ocasiones de manera directa no se pueden realizar las
integrales, en
otras ocasiones parece ser que pudiéramos integrar de
manera inmediata debido a que a primera inspección
encontramos similitud con las formulas que tenemos en las tablas
de formulas. Inclusive existen algunas de las mismas formulas que
podemos deducir mediante algunas técnicas,
como la que en esta ocasión nos ocupa, veamos el siguiente
ejemplo: Deduce la siguiente formula:
Pensemos en una sustitución que podamos realizar en la
integral de tal forma que nos permita una integración inmediata. Recordemos que:
observemos que sucede si hacemos un cambio de
variable que nos conduzca a el uso de esta sustitución,
concretamente, sustituyamos
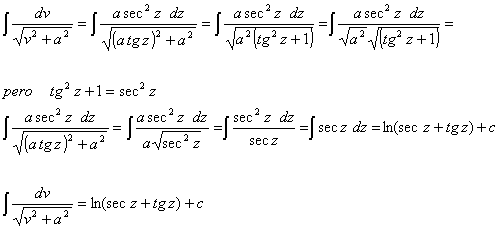
Recordemos que a 
lo también queda expresado
como:
de donde
donde la nueva c se ha juntado con la constante generada con
el logaritmo:
al igual que esta integral se pueden encontrar de la misma
forma algunas otras, vale la pena seguir la siguiente
recomendación:
hemos de aclarar que esas sustituciones surgen al igual que la
sustitución del ejercicio anterior, de observación y comparación de las
propiedades trigonométricas:
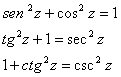
Calcular la siguiente integral y comprobar
como podemos comprobar la integración no se puede
realizar de manera inmediata. Antes de realizar alguna
sustitución valdría la pena hacer alguna
factorización en el radical
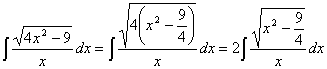
realizando la sustitución
por lo tanto:
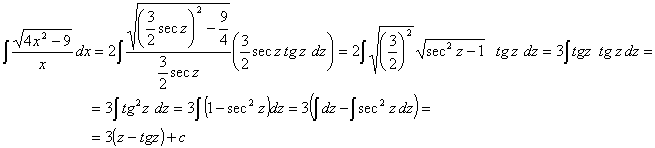
como 
entonces:
del triangulo rectángulo
siguiente identificamos:
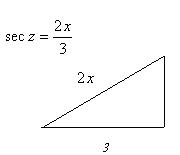
la hipotenusa es 2x y el cateto adyacente es 3 por lo
tanto el cateto opuesto es igual a:
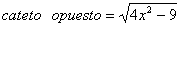
por lo que
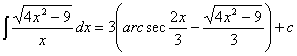
Comprobación del resultado.
simplificando tenemos:
Se sugieren los siguientes ejercicios: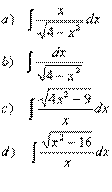 
Sustitución
trigonométrica
A menudo es posible
hallar la antiderivada de una función
cuando el integrando presenta expresiones de la forma:
Se elimina el radical haciendo la sustitución
trigonométrica pertinente; el resultado es un integrando
que contiene funciones
trigonométricas cuya integración nos es
familiar. En la siguiente tabla se muestra
cuál debe ser la sustitución:
Expresión en el | Sustitución |
|
|
|
|
|
|
Página siguiente  |