- Distribución
normal (campana de gauss) - Factores de
seguridad - Criterios del
reglamento del ACI 318 - Referencia
bibliografica
1.
INTRODUCCIÓN
Un concepto muy
importante que hay que tener en cuenta actualmente es que los
métodos de
diseño
estructural en concreto son
probabilísticas.
Al ser el concreto un material heterogéneo, está
sujeto a la variabilidad de sus componentes así como a las
dispersiones adicionales por las técnicas
de elaboración, transporte,
colocación y curado en obra.
La resistencia del
concreto bajo condiciones controladas sigue con gran
aproximación la distribución probabilística
Normal.
En la tabla 1 se muestran las principales fuentes de
variación de la resistencia en compresión del
concreto
Tabla1: Principales fuentes de
variación de la resistencia del concreto

2.
DISTRIBUCIÓN NORMAL (CAMPANA DE GAUSS)
Hoy en día está demostrado que el comportamiento
de la resistencia del concreto a compresión se ajusta a la
Distribución Normal (Campana de Gauss), cuya
expresión matemática
es:

Donde :
DS = Desviación Estándar
XPROM= Resistencia Promedio
X = Resistencia de ensayo
e = 2.71828
ï = 3.14159
Al graficar la ecuación anterior obtenemos una grafica
especial el cual tiene algunas características:
– Es simétrica con respecto a m
– Es asintótica respecto al eje de las abscisas
– La forma y tamaño va a depender de Ds
El siguiente gráfico muestra la curva
normal para diferentes valores de Ds,
teniendo un mismo u entonces podemos concluir que a medida que
aumenta el Ds el grado de dispersión que existente las
resistencia de las probetas es mayor el cual tiende a alejarse
del promedio

La Desviación estándar está
definida como:

Donde:
Ds = Desviación Estándar
Xprom = Resistencia Promedio
X = Resistencia individual
n = Número de ensayos
Este parámetro nos indica el grado de dispersión
existente entre la resistencia a compresión para un
determinado f"c.
Coeficiente de variación, tiene como
expresión:

Donde:
DS = Desviación Estándar
XPROM= Resistencia Promedio
Este parámetro no permite predecir la variabilidad
existente entre los ensayos de
resistencia La distribución normal permite estimar
matemáticamente la probabilidad
de la ocurrencia de un determinado fenómeno en función de
los parámetros indicados anteriormente, y en el caso del
concreto se aplica a los resultados de resistencias.
Ejemplo 1
Calcular la Desviación estándar, el promedio y
coeficiente de variación conociendo los resultados de las
resistencias en compresión del promedio de las probetas de
concreto.
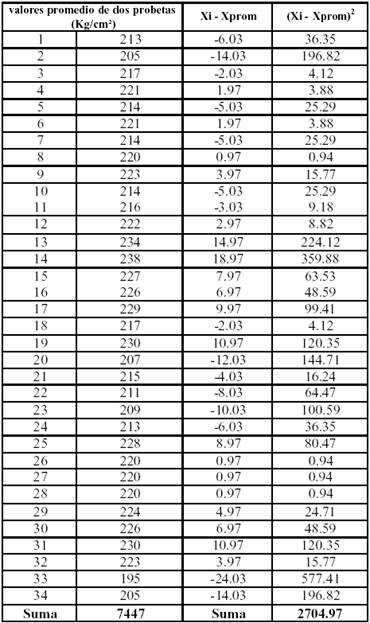
Para hallar el Xprom, utilizaremos la expresión:

La desviación estándar será:

Por último la variación será:

Ejemplo 2
Conociendo los resultados de las resistencias en
compresión de 434 probetas de concreto, se puede asociar
con el comportamiento Normal?
Lo primero que se tiene que hacer en estos casos es determinar
la frecuencia de cada resistencia a la compresión desde la
resistencia más baja hasta las más alta

Agrupando las 434 probetas por el número de frecuencias
obtuvimos un depurado de 72 probetas, calculamos sus
parámetros básicos:
Xprom = 364 Kg/cm²
Ds = 27.1 Kg/cm²
Luego procedemos a graficar las resistencias versus la
frecuencia de estos, obteniendo la siguiente gráfica:

Página siguiente  |
