Tolerance Stack (página 2)

Using general tolerances that apply to
locating dimensions have four inherent problems. These problems
are:

• Undesirable tolerance accumulation

• Lack of clear measurement origins

• Tolerancing points in space that cannot be
  measured

• Wedge shaped tolerance zones

The next drawing illustrates these four
problems. Imagine trying to draw a shadowgraph to inspect the R30
on an optical comparator. The general tolerances do not relate to
the datums shown on the part so you would be guessing at where to
start. Also, since the 50 and the 75 dimensions would use the
+0.2 general tolerance, it is not clear where the center of the
R30 is. Anyone who has ever tried to inspect a part such as this
will tell you that once the part is produced, it is virtually
impossible to reproducibly measure the R30 value and its
location. Again, once you have the part in your hand, try to
determine what origin to use when measuring the 45° angled
surface.

These problems may be overcome by using
general geometric tolerances to locate features. By using a
general profile tolerance, the tolerances apply to the surface of
the part, something you can touch. General + tolerances are often
to imaginary points in space.

ISO 2768 invokes a set of general
tolerances based on a study of common machine shop practices. If
the part does not meet these general tolerances, the part might
still be accepted if it seems to work in its' function. This
approach may work in Europe, but with our present requirements
for Cp and Cpk, it would never fly. Avoid referencing this
standard. Coplanarity:ISO uses flatness and the term
"common zone" to control
coplanarity.

Locating plane
surfaces

Y14.5 uses profile of a surface to locate
planes. Although ISO does not
disallow using profile of a surface to locate planes,
traditionally position is used. In Y14.5, position may only be
used to locate features of size and bounded features such as hex,
square and 'D' shaped holes. As mentioned earlier, the ISO
definition of a profile of a surface tolerance zone creates a
rounded corner condition while Y14.5 creates a sharp corner
condition. Concentricity and
symmetry

Y14.5 requires that all derived median
points must be within the specified tolerance for concentricity
and symmetry. This makes inspection very time consuming and
should be avoided. ISO's definitions of concentricity and
symmetry are identical to the Y14.5 definition of position for
features shown coaxial or symmetric. Also, ISO permits the use of
maximum material and least material for concentricity and
symmetry whereas Y14.5 does not.  Additional differences
in ISO

ISO as yet does not have symbols for all
around, between, controlled radius, counterbore, countersink,
depth, statistical tolerance and tangent plane. ISO does not
include axis or center plane straightness, composite profile and
a mathematically defined datum feature. Datum referencing with
position is optional. Ambiguous order of datums is permitted in
datum referencing if no vertical lines are present in the feature
control frame where datums are referenced. Target lines use
different symbology. Angular tolerances do not include form
control. A leader when specifying a datum feature or geometric
tolerance may indicate a centerline. Numbers are separated from
decimal fractions by a comma. The application of geometric
tolerances to threads is not defined in ISO. First angle
projection is the default in ISO whereas the ASME standards
default to third angle projection. The definition of composite
does not agree in the two standards.

(Day, 1997 – 2008)

Tolerance
Stack

It is of interest to examine how the ASME Y14.5M-1994
standard and its companion ASME Y14.5.1M-1994 treat this subject.
The former contains a very short Section 2.16, pp 38-39, which
briefly mentions the basic forms of arithmetic and statistical
tolerancing in connection with a new drawing symbol indicating a
statistical tolerance, namely · ST . This symbol is
intro-

duced there for the first time and it is to be expected
that future editions of this standard will move toward taking
advantage of statistical tolerance stacking. At this point the
above symbol indicates that tolerances set with this symbol are
to be monitored by statistical process control methods. How that
is done is still left up to the user. Other symbols with similar
intent are already in use in various
companies.

Typically any exposition on tolerancing will include the
two cornerstones, arithmetic and statistical tolerancing. We will
make no exception, since these two methods provide conservative
and optimistic benchmarks, respectively.

Under arithmetic tolerancing it is assumed that the
detail part dimensions can have any value within the tolerance
range and the arithmetically stacked tolerances describe the
range of all possible variations for the assembly criterion of
interest.

In the basic statistical tolerancing scheme it is
assumed that detail part dimensions vary randomly according to a
normal distribution, centered at the midpoint of the tolerance
range and with its ±3s spread covering the tolerance
interval. For given part dimension tolerances this kind of
statistical analysis typically leads to much tighter assembly
tolerances, or for given assembly tolerance it requires
considerably less stringent tolerances for detail part
dimensions, resulting in significant savings in cost or even
making the difference between feasibility or infeasibility of a
proposed design.

Practice has shown that the results are usually not
quite as good as advertised. Assemblies often show more variation
in the toleranced dimension than predicted by the statistical
tolerancing method. The causes for this lie mainly in the
violation of various distributional assumptions, but sometimes
also in the misapplication of the method by not understanding the
assumptions. Not wanting to give up on the intrinsic gains of the
statistical tolerancing method one has tried to relax these
distributional assumptions in a variety of ways. As a consequence
such assumptions are more likely to be met in
practice.

One such relaxation is to allow other than normal
distributions. Such distributions essentially cover the tolerance
interval with a wider spread, but are still centered on the
tolerance interval midpoint. This results in somewhat less
optimistic gains than those obtained under the normality
assumption, but it usually still yields better results than those
given by arithmetic tolerancing, especially for tolerance chains
involving many detail parts.

Another relaxation of assumptions concerns the centering
of the distribution on the tolerance interval midpoint. The
realization that it is difficult to center any process exactly
where one wants it to be has led to several mean shift models. In
these the distribution may be centered anywhere within a certain
small neighborhood around the nominal tolerance interval
midpoint, but usually it is still assumed that the distribution
is normal and its ±3s spread is within the tolerance
limits. This means that while we allow some shift in the detail
process mean we either require a simultaneous reduction in part
variability or we have to widen the tolerance interval. The mean
shifts are then stacked in worst case fashion. The variation of
the shifted distributions

is stacked statistically. The overall assembly tolerance
then becomes (in worst case fashion) a sum of two parts,
consisting of an arithmetically stacked mean shift contribution
and a term reflecting the statistically stacked part variation
distributions. It turns out that our cornerstones of arithmetic
and statistical tolerancing are special cases of this more
general model, which has been claimed (Greenwood and Chase, 1987)
to unify matters.

However, there is another way of dealing with mean
shifts which appears to be new, at least in the form presented
here. It takes advantage of statistical stacking of mean shifts
and stacking that aggregate in worst case fashion with the
statistical stacking of the part variation distributions. A
precursor to this can be found in Desmond"s discussion of
Mansoor"s (1963) paper. However, there it was pointed out that it
leads to optimistic results. We discuss the issues involved and
present several variations on that theme.

Other fixes augment the statistical tolerancing method
with blanket tolerance inflation factors with more or less
compelling reasons. It turns out that one of the above mentioned
mean shift treatments results in just such an inflation factor,
with the size of the factor linked explicitly to the amount of
tolerated mean shift.

When dealing with tolerance stacking under mean shifts
one has to take special care in assessing the risk of
nonassembly. Typically only one tail of the assembly stack
distribution is significant when operating at one of the two
worst possible assembly mean shifts. One can take advantage of
this by reducing the assembly tolerance by some small amount. We
indicate briefly how this is done but refer to Scholz (1995) for
more details.

(Scholz, 1995)

Chain
Dimensioning

Chain Dimensioning is the method of dimensioning the
beginning of the next feature from the end of the last. It seems
pretty straight forward but some may not realize that this gives
the greatest amount of variation. The illustration below shows a
simple revolved part dimensioned using this method. The part
shown was modeled to have a mean distance of 3.500?
between surfaces A and B. Adding together the
tolerances of the three intermediate dimensions, you will see
that the actual variance is +/- .015?. This would make the
maximum distance between A and B to be
3.515?. This may not seem like a lot but it may be enough
to affect the overall performance of the
design.

Base Line
Dimensioning

Base Line Dimensioning gives you a better result
then Chain Dimensioning. With Base Line
Dimensioning each feature is dimensioned independently from
each other, all off the same origin. By using this method you are
creating less variance between features since the actual variance
is the tolerance of the two features added together. Using the
same part as before, this time using base line dimensioning, the
actual variance is +/- .010? because you are only going to
add the tolerance of the dimension that affects A to the
tolerance of B. This will make the maximum distance
between A and B to be 3.510". This is better
then before, but we can sill do better.

Direct
Dimensioning

Direct Dimensioning will give you better control
over the finished dimensions of the part since you will be
tolerancing the specific features you wish to control. In this
part we have been concerned about the true distance between
A and B, so why don"t we just control that
dimension. By adding adding a dimension between A and
B we cut the variance down to +/-.005?, this would
give us a maximum distance of 3.505?.  I am not
saying that you should not use any of the two previous methods.
Each method has it"s place and you should consider what variance
you can accept when dimensioning your parts.

Dimensional
Limits Related to an Origin

As you saw in the previous sections how you dimension a
part can seriously effect the final results. Where a dimension
originates from can also have an effect on the final shape of the
part. The method shown below designates a feature as the
dimension origin using a Dimension Origin Symbol instead
of an arrow. This is not the same as designating a "datum" as you
would in GT&D (we will cover Datums at a later date) instead
this method is used to create a tolerance zone that the feature
must lie. Look at the 1.000+/-.100 dimension, the shorter
side of the part is being designated at the origin. This means
that the tolerance applies to the other side of the dimension,
the longer side.

The figure below better illustrates what the tolerance
zone created by designating the shorter side as the dimension
origin. The entire longer surface indicated must lie within the
tolerance zone created.

In case your wondering why it makes a differences as to
what side the dimension originates, the view below shows how the
part could be made of the other side was designated. Big
difference, right?

Designating a
Origin

Now that you know what is a dimension origin, you
probably want to know how to add the symbol to a dimension. I
must admit, this stumped me for a while and I must thank Josh
Mings at Solidsmack for
helping me figure it out. The key is to make sure that your the
intended dimension is not set as a Smart Dimension. If you
right-click on the dimension and you see Smart Dimension
selected, de-select it. Then on the dimension itself, when you
select it, you will see nodes on each arrowhead.

When you right click on the node, you will be presented
with the available arrowhead types. Click the Dimenension
Origin Symbol, the one that looks like an empty
circle.

(Geek, 2008)

Notation and
Problem Formulation

The tolerance stacking problem arises in the context of
assemblies from interchangeable parts because of the inability to
produce or join parts exactly according to nominal. Either the
relevant part dimension varies around some nominal value from
part to part or it is the act of assembly that leads to
variation.

For example, as two parts are joined via matching hole
pairs there is not only variation in the location of the holes
relative to nominal centers on the parts but also the slippage
variation of matching holes relative to each other when
fastened.

Thus there is the possibility that the assembly of such
interacting parts will not function or won"t come together as
planned. This can usually be judged by one or more assembly
criteria, say G1,G2, . . .. Here we will be concerned with just
one such assembly criterion, say G, which can be viewed as a
function of the part dimensions L1, . . ., Ln. A simple example
is illustrated in Figure 1, where n = 6 and

G = L1 – (L2 + L3 + L4 + L5 + L6)

= L1 – L2 – L3 – L4 – L5 – L6 (1)

is the clearance gap of interest. It determines whether
the stack of cogwheels will fit within the case or not. Thus it
is desired to have G > 0, but for functional performance
reasons one may also want to limit G from above.

A graphical representation of equation (1) is given in
Figure 2, where the various dimensions L1, L6, L5, L4, L3, and L2
are represented by vectors chained together, L1 butting into L6,
L6 butting into L5 (after changing direction), L5 butting into
L4, L4 butting into L3, and L3 butting into L2.

The remaining gap to make L2 butt up to L1 is the
assembly tolerance gap of interest, namely G. This type of
linkage is called a tolerance path or tolerance chain. Note that
the arrows point right for positive contributions and left for
negative ones.

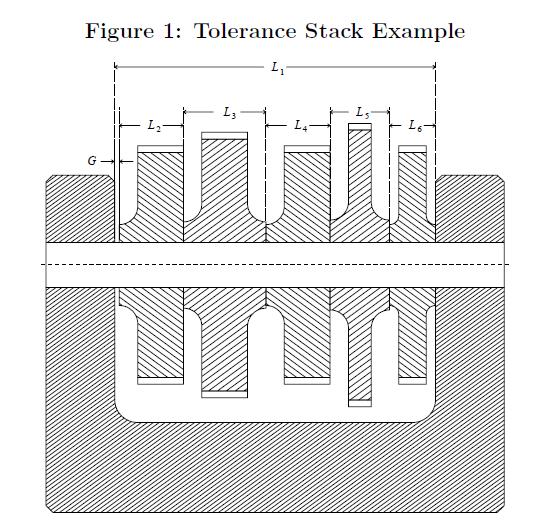
As was pointed out before, the actual lengths Li may
differ from the nominal lengths ?i by some amount. If there is
too much variation in the Li there may well be significant
problems in satisfying G > 0. Thus it is prudent to limit
these variations through tolerances. Such tolerances, Ti,
represent an "upper limit" on the absolute difference between
actual and nominal values of the ith detail part dimension, i.e.,
|Li – ?i| = Ti. It is mainly in the interpretation of this last
inequality that the various methods of tolerance stacking
differ.

The nominal value ? of G is usually found by replacing
in equation (1) the actual Li"s by the corresponding nominal
values ?i, i.e.,

? = ?1 – ?2 – ?3 – ?4 – ?5 – ?6.

If the objective is to achieve a gap G that is positive
and not too large (for other functional reasons) then one would
presumably design the assembly in such a way that the nominal gap
? satisfies this goal, with the hope that the actual gap G be not
too different from ?. Thus the quantity G – ? is of considerable
interest. It can be expressed as follows in terms of _i = Li –
?i, the detail deviations from nominal,

G – ? = (L1 – ?1) – (L2 – ?2) – (L3 – ?3)

– (L4 – ?4) – (L5 – ?5) – (L6 – ?6)

= _1 – _2 – _3 – _4 – _5 – _6 .

The main question of tolerance stacking is the bounding
of the assembly error or assembly misfit G – ? when given
tolerance bounds Ti on the detail part errors, i.e. |_i| = |Li –
?i| = Ti. In the following we will present several such bounds
and state under what assumptions they are valid. Before doing so
we generalize the above example to a generic tolerance chain and
in the process widen the scope to smooth sensitivity analysis
problems.

Above we had an assembly with a stack of six parts that
involved one positive and five negative contributions. This can
obviously be generalized to n detail parts with various
configurations of positive and negative contributory directions
in the tolerance chain. Hence in general we have:

G = a1L1 + a2L2 + a3L3 + . . . + anLn,

F (X1,X2, . . . ,X7) = Y Y

where the coefficients a1, . . . , an are either +1 or
-1, independently of each other. Our introductory example had n =
6 and a1 = 1, a2 = . . . = a6 = -1.

This then leads to

as the primary object of tolerance stack
analysis.

From here it is only a small step to extending these
methods to sensitivity analysis in general. Those not interested
in this generalization can skip to the beginning of the next
section.

Rather than butting parts end to end and forming an
arithmetic sum of ± terms with some resultant output G, we
can view this relation as a more general input/output relation.
To get away from the restrictive notion of lengths we will use
X1, . . .,Xn as our inputs (in place of L1, . . ., Ln) and Y (in
place of the gap G) as our output. However, here we allow more
general rules of composition, namely

Y = f(X1, . . .,Xn) ,

where f is some known, smooth function which converts
the inputs X1, . . .,Xn into the output Y . This is graphically
depicted in Figure 3. As an example 7 of such a more general
relationship consider some electronic device with components
(capacitors, resistances, etc.) of various types. There may be
several performance measures for such a device and Y may be any
one of them. Given the performance ratings X1, . . .,Xn of the
various components, physical laws describe the output Y in some
functional form, which typically is not linear.

The design of such an electronic device is based on
nominal values, ?1, . . . , ?n, for the component ratings.
However, the actual characteristics X1, . . .,Xn will typically
be slightly different from nominal, resulting in slight
deviations for the actual Y = f(X1, . . .,Xn) from the nominal ?
= f(?1, . . . , ?n). Since these component deviations are usually
small we can reduce this problem to the previous one of
mechanically stacked parts by linearizing f, namely
use

Note: for this linearization to work we have to assume
that f has continuous first partial derivatives at (?1, . . . ,
?n).

Aside from the term a0 we have again the same type of
arithmetic sum for our "assembly" criterion Y as we had in the
mechanical tolerance stack.

However, here the ai are not restricted to the values
±1. The additional term a0 1 does not present a problem as
far as variation analysis is concerned, since it is constant and
known.

Again we like to understand how far Y may vary from the
nominal ? =

f(?1, . . . , ?n). From the above we have

i.e., just as before, the only difference being that the
ai are not restricted to ±1. Since all the tolerance
stacking formulas to be presented below will be 1it is based on
the nominal and known quantities ?1, . . . , ?n given in terms of
these ai and since nowhere use was made of ai = ±1, it
follows that they are valid for general ai and thus for the
sensitivity problem.

There are situations in which a functional relation Y =
f(X1, . . .,Xn), although smooth, is not very well approximated
by a linear function, at least not over the range of variation
envisioned for the Xi. In that case one could use a quadratic
approximation to capture any relevant curvature in f. Tolerance
stacking methods using this approach are covered in Cox (1986).
These methods are fairly complex and still quite restrictive in
the assumptions under which they are valid. Of course, it may be
possible to extend these methods along the same lines as
presented here for linear tolerance stacks.

As noted above, the linearization will work only for
smooth functions f.

To illustrate this with a counterexample, where
linearization fails completely, consider the function

which can be viewed as the distance of a hole center
from the nominal origin (0, 0). This function does not have
derivatives at (0, 0), its graph in 3-space looks like an upside
cone with its tip at (0, 0, 0). There can be no tangent plane at
the tip of that cone and thus no linearization. Another example
where such linearization fails is discussed in Altschul and
Scholz (1994). It involves hinge mating and the problem arises
due to simultaneous and thus minimum gap requirements.

In presenting the tolerance stacking formulas we will
return to using Li and ?i for the part dimensions and nominals.
Those that wish to apply these concepts to sensitivity analysis
should have no problem replacing

Tolerance
Stacking Formulas

In this section we will present various formulas for
tolerance stacking. By Tolerance stacking we mean a rule that
combines the detail tolerances Ti Into an assembly tolerance
Tassy. Typically Tassy is a monotone increasing Function of the
Ti. Thus, if the resulting Tassy is too large, one can counteract
That by reducing all or some of the Ti, which usually makes for
costlier Part production. On the other hand, if Tassy is smaller
than required for Successful assembly fit, and then one can
loosen the detail tolerances Ti, with Some possibility of cost
reduction.

Why do we have more than one formula for tolerance
stacking and why So many? One reason for this is that these
methods have evolved and are Still evolving, partly responding to
economic pressures and partly because of The nature of the
problem. Namely, it all depends on what assumptions one Is
willing to make.

Fewer assumptions entail broader applicability but one
also will get less Out of a tolerance stack analysis, i.e., one
will wind up with fairly wide Assembly tolerance limits or, when
trying to counteract that through the Ti, With very tight and
thus costly detail tolerance requirements.

With more knowledge about the manufacturing processes
one may feel Comfortable with more assumptions, resulting in
tighter assembly tolerance Limits or, if those can be relaxed,
with looser detail tolerance requirements.

Thus it is very important to be aware of the assumptions
behind the various Methods. We will begin the presentation of
stacking methods with the Worst case or arithmetic method, which
tends to be most conservative. This Is followed by the
conventional RSS or statistical tolerance stacking method, Which
tends to be on the optimistic side. This results from imposing
some

Rather stringent assumptions. If the arithmetic stacking
method gives satisfactory Assembly tolerance results, then there
is little motivation to try any Of the other methods, except
possibly to relax detail tolerances to achieve Cost reduction. If
the RSS method does not give satisfactory assembly tolerance
Results, then any of the other methods will not make matters any
Better. Then the only recourse is to tighten detail tolerances
or, if that is Not feasible, change the design.

After discussing these two basic and well known methods
we will discuss Several hybrid tolerance stacking methods which
impose assumptions which Are more likely to be met in practice.
As a result the assembly tolerances lie Somewhere between those
corresponding to the two classical methods.

Arithmetic or
Worst Case Tolerance Stacking

The validity hinges solely on the above assumption.
Thus, no matter how the detail dimensions Li deviate from their
nominal values ?i within the Constraint |Li – ?i| = Ti, the
difference |G – ?| is guaranteed to be bounded

By T This guarantee is the main strength of this method.
However, one Should not neglect to make sure that the assumptions
are met, i.e., detail Parts need to be inspected to see whether
|Li – ?i| = Ti or not.

The main weakness of the method is that
Tarith

assy grows more or less linearly

With n. This is most easily seen when the detail part
tolerance contributions

By inverting this we get

Tdetail = Tarithassy/n

,

Which tells us how to specify detail tolerances from
assembly tolerances. As assemblies grow, i.e., as n gets large,
these requirements on the detail

Tolerances can get quite severe.

The linear growth of Tarith assy results from assuming a
devil"s advocate position

In deriving the formula for Tarith assy , namely by
always taking the detail Part variation in such a way as to make
the assembly criterion G differ as Much as possible from ?. This
is the reason for the method"s alternate name: Worst case
tolerancing.

If the detail tolerances are not all the same, it is
more complicated to Arrive at appropriate detail tolerances
satisfying a given assembly tolerance Requirement. For example,
suppose

So that

For i = 2, . . . , n. Thus relaxing or tightening Tarith
assy by some factor affects all Detail tolerances Ti by the same
factor.

One may also want to treat the detail tolerances Ti in a
more differentiated Manner, i.e., leave some as they are and
reduce other significantly in order to Achieve the desired
assembly tolerance. This easily done in iterative fashion Using
the forward formula (2).

The above considerations on how to set detail tolerances
based on assembly Tolerance requirements can be carried out for
the other types of tolerance Stacking as well and we leave it up
to the reader to similarly use the various Tolerance stacking
formulas in reverse.

RSS Method or
Statistical Tolerancing

Under this method of tolerance stacking a very important
new element is Added to the assumptions, namely that the detail
variations from nominal Are random and independent from part to
part. In some sense this is a Reaction to the worst case paradigm
of the previous section which many feel Is overly conservative.
It is costly in the sense that it often mandates very Tight
detail tolerances.

That all deviations from nominal should arrange
themselves in worst case Fashion to yield the most extreme
assembly tolerance is a rather unlikely Proposition.
However, it had the benefit of guaranteeing the resulting
assembly Tolerance. Statistical tolerancing in its classical form
operates under two Basic assumptions:

Centered Normal Distribution: Rather than
assuming that the Li can Fall anywhere within the tolerance
interval [?i – Ti, ?i + Ti], even to The point that someone
maliciously and deliberately selects parts for Worst case
assemblies, we assume here that the Li are normal random Variables,
i.e., vary randomly according to a normal distribution,
centered On that same interval and with a ±3s
spread equal to the span

Normal
Distribution over Tolerance Interval

Of that interval, so that 99.73% of all Li values fall
within this interval, See Figure 4. The nature of the normal
distribution is such that The Li occur with higher frequency in
the middle near ?i and with less Frequency near the interval
endpoints. The match of the ±3s spread With the span of
the detail tolerance span is supposed to express that Almost all
parts will satisfy the detail tolerance limits.

Deviations from nominal are not a deliberate act but
inadvertent and Due to forces not under our control. If these
forces are several and Influence the final deviation from the
nominal value in independent Fashion, then there are theoretical
reasons (the central limit theorem of Probability theory)
supporting a normal distribution for Li. However, It may not
always be reasonable to assume that this normal distribution Is
exactly centered on the nominal value. This objection is the
starting Point for some of the hybrids to be discussed
later.

Independent Detail Variation: The independence
assumption is probably The most essential cornerstone of
statistical tolerancing. It allows For some cancellation of
variation from nominal.

Treating the Li as random variables, we also demand that
these random Variables are (statistically) independent. This
roughly means that the deviation Li – ?i has nothing to do with
the deviation Lj – ?j for i _= j. In particular, the deviations
will not be mostly positive or mostly

Negative. Under independence we expect to get a mixed
bag of negative And positive deviations of various sizes which
essentially leads to some Variation cancellation in the adding
process. Randomness alone does Not guarantee such cancellation,
especially not when all part dimension Show random variation in
the same direction. This latter phenomenon Is exactly what the
independence assumption intends to exclude.

Typically the independence assumption is reasonable when
part dimensions Pertain to different manufacturing/machining
processes. However, Situations can arise where this assumption is
questionable. For Example, several similar/same parts (coming
from the same process) Could be used in the same assembly. If
this process is affected by a Mean shift, then this mean shift
will accumulate in worst case fashion For all parts coming from
that process. Thermal expansion also tends To affect different
parts similarly.

Under the above assumptions of centered normality and
independence we Can give the following statistical tolerance
stacking formula

Where the latter formulation holds when ai = ±1
for all i = 1, . . . , n. The Term RSS for this type of stacking
stems from its abbreviation for Root Sum Of Squares.

Typically Tstatassy is significantly smaller than
Tarithassy . For n = 3 the magnitude Of this difference is easily
visualized and appreciated by a rectangular Box with side lengths
T1, T2 and T3. To get from one corner of the box to The
diagonally opposite corner, one can traverse the distanceT21 +
T22 + T23 Along that diagonal or one can go the long way and
follow the three edges With lengths T1, T2, and T3 for a total
length Tarith assy = T1 + T2 + T3 as in Figure 5.

This reduction in assembly tolerance comes at a small
price. Whereas Tarithassy bounds the assembly deviation |G – ?|
with absolute certainty, the

Statistical tolerance stack Tstat assy bounds |G-?| only
with some high assurance, Namely with .9973 probability. The
crookedness of .9973 results from the fact That the variation of
G around ? is again normal2 and that ±Tstat assy
represents

a ±3s range for that variation. The 3 in 3s is a
nice round number, but The probability content (.9973) associated
with it is not. One cannot have it Both ways.

The small price, going from absolute certainty down to
99.73%, is not all. Recall that normal part variation, centered
on the tolerance interval with Ti = 3si, and independence of
variation from part to part are assumed as Well.

RSS Method with
Inflation Factors

Practice has shown that arithmetic tolerancing tends to
give overly conservative Results and that the RSS method is too
optimistic, i.e., is not living up To the proclaimed 99.73%
assembly fit rate. This means that actual assembly Stack
variations are wider than indicated by the ? ±Tstat assy
range. The reasons

For this have been examined from various angles. We list
here

Independence: An important aspect of statistical
tolerance stacking is the Independence of variations from nominal
for the detail parts participating In an assembly.

3si = T i: Does the ±Ti range
really represent most or all of the detail part
Variation?

Normality: Is the detail part variation
reasonably represented by the normal Distribution?

Centered process: Is the process of part
variation centered on the nominal, the midpoint of the tolerance
interval?

One reason for a reduction in the efficacy of
statistical tolerance stacking could be that the independence
assumption is violated. We will not dwell on that issue too much
except for some very specific modes of dependence such as random
mean shifts or tooling errors. Dependence can take so many forms
that it is difficult to cope with it in any systematic way.
However, we will return to this later when we discuss mean shifts
that are random.

One other possible reason for the optimism of the RSS
method is that one basic premise, namely Ti = 3si, is not
fulfilled. This can come about when manufacturing process owners,
asked for the kind of tolerances they can hold, sometimes will
respond with a ±Ti value which corresponds to a
±2si range.

Reasons for this could be limited exposure to actual
data. Values outside the ±2si range are hardly ever
experienced3 and if they do occur they may be rationalized away
as an abnormality and then disappear from the conscious record.
Thus, if Ti is specified with the misconception Ti = 2si, then Ti
is too small by a factor 1.5. To correct for this, Bender (1962)
suggests to multiply

the ±Tstat assy value by 1.5and calls this
process "benderizing," i.e.,

The assumptions behind this formula are the same as
those for (3) except that detail part tolerances correspond to
±2si rather than ±3si normal variation
ranges.

This inflation factor 1.5giv es up a fair amount of the
gain in Tstat assy. In fact, for n = 2 it is more conservative
than arithmetic tolerance stacking, since

Of course, some may say that we should have used a
1.5fac tor on the right side as well, because those tolerances
are also misinterpreted. The rationale for the inflation factor
is not altogether satisfactory, since it is based on ignorance
and suppositions about meanings of Ti. What we have here is
mainly a communications breakdown. If we do not have data about
the part process capabilities, any tolerance analysis will stand
on weak legs. If we have only limited data, then it should still
be possible to avoid the mixup of 2si with 3si variation ranges.
In fact, upper confidence bounds on 3si, based on limited data,
will be quite conservative and thus should lead to conservative
values Tstatassy when using such confidence bounds for
Ti.

Although the normality assumption is well supported by
the central limit theorem4, there are processes producing detail
part dimensions which are not normally distributed. Some such
processes come about through tool wear, where part dimensions may
start out at one end of the tolerance range and, as the tool
wears, eventually wind up at the other end. The collection of
such parts would then exhibit a more uniform distribution over
the tolerance range.

Some people have simply postulated a somewhat wider
distribution over the ±Ti tolerance range mainly for the
purpose of obtaining an inflation factor to the RSS formula, see
Gilson (1951), Mansoor (1963), Fortini (1967), Kirschling (1988),
Bjorke (1989), and Henzold (1995). Several such distributions are
illustrated in Figure 6 with the corresponding inflation factors
c. Of course, one may find that different detail part variations
warrant different inflation factors. Using such inflation factors
c = (c1, . . . , cn) for the n detail parts leads to the
following modified statistical tolerance stacking
formula:

The underlying assumptions are that the part variations
are independent and are characterized by possibly diverse
distributions centered on the part tolerance intervals. These
distributions, not necessarily normal, mostly cover the
respective part tolerance intervals, either completely or by
their ±3si ranges, see Figure 6.

The interpretation of this assembly tolerance stack is
as before. Namely, one can expect that 99.73% of all assembly G
gap values fall within ? ± Tstatassy(c). Although
the individual contributors to the stack may no longer be
normally distributed we can still appeal to the central limit
theorem to conclude that G is approximately normally distributed.
Since the word "limit"
in central limit theorem implies that the number of terms being
added should be at least moderately large, it is worth noting
that in many situations one can get fairly reasonable normal
approximations already for n = 2 or n = 3 stacking
terms.

One notable problem case among the distributions
featured in Figure 6 is the uniform distribution. In that case
the sum of two uniformly distributed random variables will in
general have a trapezoidal density, which on theface of it cannot
qualify as being approximately normal. If the two uniform
distributions have the same width then this trapezoidal density
becomes triangular. See the left side of Figure 7 where the top
panel gives the cumulative distribution and its normal
approximation and the bottom panel shows the corresponding
densities for the sum of two random variables, uniformly
distributed over the interval (0, 1). The right side of Figure 7
shows the analogous comparisons for the sum of three such uniform
random variables.

Although the density comparison shows strong
discrepancies for the sum of two uniform random terms, there
appears to be much less difference for the cumulative
distribution, since the undulating errors, visible for the
densities, cancel out in the probability accumulation process.
Thus the central limit theorem could be appealed to even in that
case, if one is content

with somewhat rougher probability
approximations

Note also that the normal approximation spreads out
further than the approximated distribution. This would result in
conservative assembly risk assessment. Rather than .27% of
assemblies falling out of tolerance (under the normal
approximation) it would be actually less under uniform detail
part variation.

Before using inflation factors based on specific
distributions one should make sure that such distributions are
really more appropriate than the customary normal distribution.
Such judgments should be based on data. If one has such validated
concerns they may affect just one or two such contributors in (5)
and leaving most other c factors equal to one. Note that c
factors larger than one increase the assembly tolerance
stack.

We view formula (5) mainly as a useful extension to
formula (3) for just such situations where normality does not
hold for all detail part dimensions.

This way the behavior of one part process alone will not
preclude us from performing a valid statistical tolerance
analysis.

If one uses such distributions solely for getting some
sort of inflation or protection factor without having any other
justification, one should drop that distribution pretense and
just admit to using an inflation factor for just such protection
purpose.

Some of the distributions portrayed in Figure 6 require
some comments or explanation. The uniform distribution can in
some sense be viewed as a most conservative description of
variation over a fixed interval. Among all symmetric, unimodal5
distributions over such an interval it has the most spread or the
largest standard deviation si.

The trapezoidal density is uniform on the interval [?i –
kTi, ?i + kTi], where k is some number in [0, 1], and the density
falls off linearly to zero over [?i + kTi, ?i + Ti] and [?i – Ti,
?i – kTi]. The uniform and triangular density are special cases
of the trapezoidal one.

The elliptical density6 consists of half an ellipse and
is characterized by the requirement that one axis of the ellipse
straddles the interval ?i ±Ti and its other half axis has
length 2/(pTi).

Aside from the normal distribution the Student t-density
is the only one among the illustrated distributions which has an
unbounded range. This raises the issue of how to match up the
range of such distributions with the finite range [?i-Ti, ?i+Ti].
In the normal case it has been traditional to take Ti = 3si with
the normal distribution centered on ?i. With that identification
99.73% of all detail parts of type i will vary within [?i-Ti,
?i+Ti]. In the case of the Student t-distribution we have two
options. We can either scale the t-distribution to match the
probability content of .9973 over [?i -Ti, ?i +Ti] or we can
again let Ti = 3si. In the former approach we will wind up with
c-factors that are less than one, because each si would typically
be much smaller than Ti/3. The trouble with this approach is that
with limited data it is very difficult to establish that [?i –
Ti, ?i + Ti] captures 99.73% of all detail part
dimensions.

The other approch, namely Ti = 3si, is much easier to
implement with limited data and it leads to a c-factor which is
one. The ease derives from the fact that standard deviations can
be estimated with fairly limited data.

However, the smaller the data set, the less certain we
can be about the standard deviation estimate.

One detraction with using Ti = 3si is that we will tend
to see more detail parts out of tolerance. In using statistical
tolerancing ideas there is no need to guarantee that all detail
parts are within tolerance as is required under arithmetic
tolerancing. In statistical tolerancing we only need to control
the amount of part variation. Occasional detail parts which fall
out of tolerance do not need to be sorted out. They actually may
average out just fine in the assembly. Note that the two
t-distributions illustrated in Figure 6 have different degrees of
freedom and thus different detail fall-out rate.

The beta density comprises a rich family of shapes and
for its mathematical form we refer to Scholz (1995). Here we only
considered symmetric beta densities with paramters a = ÃY
and standard deviation si = Ti/v(2a + 1.)

(Scholz, 1995)

Application

Today, most manufacturing companies are abandoning their
corporate standards on dimensioning and tolerancing in favor of
internationally recognized standards. The two major choices in
standards today are the Collection of ISO standards or ASME
Y14.5M-1994. There is currently about a 70% overlap in these two
standards. Most drawing requirements may be specified by staying
inside this overlap

The reasons for this transition include the cost
of:

• Maintaining corporate standards

• Educating vendors and employees

• Customizing new technology

• Defending interpretations

These costs are greatly reduced by using a globally
recognized standard. The challenge for the corporation is to
select a standard that is adequate for their applications and
demographics. Many companies are being forced to use ISO
standards across the board. There seems to be an assumption that
anything ISO is good. Unfortunately, not all ISO standards are
mature. This is certainly true in the area of dimensioning and
tolerancing. Those being required to adopt the ISO standards for
dimensioning and tolerancing should thoroughly understand their
current state, direction for the future and current limitations.
When a company has only modest design requirements, there is
sufficient overlap in the ASME Y14.5 and ISO standards to
adequately define undemanding parts. For more complex
applications committing to the ASME Y14.5 standard or creating a
corporate addendum, which supplements either the ISO or ASME,
standards may be required.

Several factors need to be considered when choosing a
direction for your company's standard. This matrix
illustrates many of these factors.

(Day, 1997 – 2008)

Conclusion

Most manufacturing companies are abandoning their
corporate standards on dimensioning and tolerancing in favor of
internationally recognized standards. The two major choices in
standards today are the Collection of ISO standards or ASME
Y14.5M-1994. We learn some of the methods most used and we
differentiate the both to choose wish one is appropriate for you
company or job.

Sources

http://www.theswgeek.com/2008/09/03/standards-wednesday-tolerance-accumulation/

http://www.tec-ease.com/tce.htm

http://www.tec-ease.com/the-new-gd&t-article.htm

http://www.stat.washington.edu/fritz/Reports/isstech-95-030.pdf

Autor:

Alan Viezcas

28 de abril de 2009