- Toma de
datos - Distribuciones de
frecuencia - Intervalos de clase y
límites de clase - Límites reales de
clases - Marca de
clase - Reglas generales
para formar las distribuciones de
frecuencia - Distribuciones de
frecuencia acumulada. Ojivas - Tipos de curvas de
frecuencia - Bibliografía
Toma de
datos
La toma de datos es la
obtención de una colección de los mismos que no han
sido ordenados numéricamente. Un ejemplo es el conjunto de
alturas de 100 estudiantes, sacados de una lista
alfabética de una universidad.
ORDENACIÓN
Una ordenación es una colocación de los
datos numéricos tomados, en orden creciente o decreciente
de magnitud. La diferencia entre el mayor y el menor de los
números se llama recorrido o rango de
los datos. Por ejemplo, si la altura mayor de los 100 estudiantes
es 74 pulgadas y la menor es de 60 pulgadas, el rango es 74 – 60
= 14 pulgadas.
Distribuciones de
frecuencia
Cuando se dispone de gran número de datos, es
útil el distribuirlos en clases o
categorías y determinar el número de
individuos pertenecientes a cada clase, que es
la frecuencia de clase. Una ordenación tabular de
los datos en clases, reunidas las clases y con as frecuencias
correspondientes a cada una, se conoce como una
distribución de frecuencias o tabla de
frecuencias. La Tabla 1 es una distribución de frecuencias de alturas
(registradas con aproximación de pulgada) de 100
estudiantes de la Universidad XYZ.
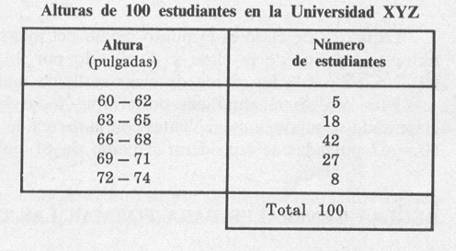
La primera clase o categoría, por ejemplo,
comprende las alturas de 60 a 62 pulgadas y viene indicada por el
símbolo 60 – 62. Puesto que 5 estudiantes tienen una
altura perteneciente a esta clase, la correspondiente frecuencia
de clase es 5.
Los datos ordenados y resumidos como en la
distribución de frecuencia anterior, se suelen llamar
datos agrupados. Aunque con el proceso de
agrupamiento generalmente se pierde parte del detalle original de
los datos, tiene la importante ventaja de presentarlos
«todos» en un sencillo cuadro que facilita el
hallazgo de las relaciones que pueda haber entre ellos, puestas
así de manifiesto.
Intervalos de
clase y límites de clase
Un símbolo que define una clase, tal como 60 – 62
de la tabla anterior, se conoce como intervalo de clase.
Los números extremos, 60 y 62, son los límites
de clase; el número menor 60 es el límite
inferior de la clase y el mayor 62 es el límite
superior. Los términos clase e intervalo de clase se
utilizan a menudo indistintamente, aunque el intervalo de clase
es realmente un símbolo para la clase.
Un intervalo de clase que, al menos teóricamente,
no tiene límite superior o inferior, se conoce como
intervalo de clase abierto. Por ejemplo, al referirse a
la edad de grupos de
individuos el intervalo de clase, «mayores de 65
años» es un intervalo de clase abierto.
Límites
reales de clases
Si las alturas se registran con aproximación de
pulgada, el intervalo de clase 60 – 62 teóricamente
incluye todas las medidas desde 59,5000… a 62,5000 …
pulgadas. Estos números, representados brevemente por los
números exactos 59,5 y 62,5, se conocen como
límites reales de clase o límites
verdaderos de clase; el menor de ellos, 59,5, es el
límite real inferior y el mayor de ellos, 62,5,
es el límite real superior.
Prácticamente, los límites
reales de clase se obtienen sumando al límite superior de
un intervalo de clase el límite inferior del intervalo de
clase contiguo superior y dividiendo por 2.
A veces, los límites reales de clase se utilizan
para simbolizar las clases. Por ejemplo, las diferentes clases de
la primera columna de la Tabla 1 podrían indicarse por
59,5 – 62,5, 62,5 – 65,5, etc. Sin embargo, con tal
notación aparece una ambigüedad, pues los
límites reales de clase no coincidirían con las
observaciones reales. Así si una observación fuese 62,5 no sería
posible discernir si pertenece al intervalo de clase 59,5 – 62,5
o al 62,5 – 65,5.
TAMAÑO O ANCHURA DE UN INTERVALO DE
CLASE
El tamaño o anchura de un intervalo de clase es
la diferencia entre los límites reales de clase que lo
forman y se conoce como anchura de clase, tamaño de
clase o longitud de clase. Si todos los intervalos
de clase de una distribución de frecuencias tienen igual
anchura, esta anchura común se representa por c.
En tal caso, c es igual a la diferencia entre dos
sucesivos límites de clase inferiores o superiores. Para
los datos de la Tabla 1, por ejemplo, el intervalo de clase es
c = 62,5 – 59,5 = 65,5 – 62,5 = 3.
Marca de
clase
Página siguiente  |
