Objetivos
Objetivo General:
Aplicar los conocimientos básicos del
cálculo, utilizando el lenguaje de programación
Matlab.
Objetivos Específicos:
Aplicar el algoritmo necesario para resolver
ecuaciones diferenciales ordinarias (EDO), a través de
una pequeña aplicación desarrollada en
Matlab.Aplicar los algoritmos necesarios para resolver EDO,
utilizando métodos numéricos, y en este caso
particular, el método de Euler y Euler mejorado, a
través de aplicaciones en Matlab.
Introducción
Las ecuaciones
diferenciales aparecen naturalmente al modelar situaciones
físicas en las ciencias
naturales, ingeniería, y otras disciplinas, donde hay
envueltas razones de cambio de una
ó varias funciones
desconocidas con respecto a una ó varias variables
independientes. Estos modelos
varían entre los más sencillos que envuelven una
sola ecuación diferencial para una función
desconocida, hasta otros más complejos que envuelven
sistemas de
ecuaciones
diferenciales acopladas para varias funciones desconocidas. Por
ejemplo, la ley de
enfriamiento de Newton y las
leyes
mecánicas que rigen el movimiento de
los cuerpos, al ponerse en términos matemáticos dan lugar a ecuaciones
diferenciales. Usualmente estas ecuaciones están
acompañadas de una condición adicional que
especifica el estado del
sistema en un
tiempo o
posición inicial. Esto se conoce como la
condición inicial y junto con la ecuación
diferencial forman lo que se conoce como el problema de
valor
inicial. Por lo general, la solución exacta de un
problema de valor inicial es imposible ó difícil de
obtener en forma analítica. Por tal razón los
métodos
numéricos se utilizan para aproximar dichas soluciones. En
este caso utilizaremos los métodos de
Euler y Euler mejorado.
Descripción de los
métodos
Método de Euler
Se llama método de
Euler al método numérico consistente en ir
incrementando paso a paso la variable independiente y hallando la
siguiente imagen con la
derivada.
La primera derivada proporciona una
estimación directa de la pendiente en Xi (ver
Gráfico Nº01).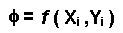 
[1]
Donde f (Xi, Yi) es la ecuación
diferencial evaluada en Xi y Yi, Tal estimación
podrá substituirse en la ecuación [2] nos queda
que:
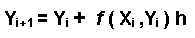[2]
Esta fórmula es conocida como el método de
Euler (punto medio). Se predice un nuevo valor de Y por medio de
la pendiente (igual a la primera derivada en el valor original de
X).
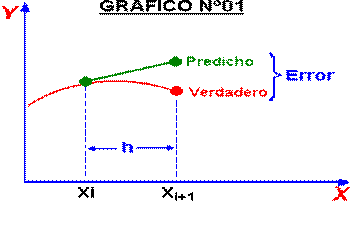
Error para el método de Euler
La solución numérica de las ecuaciones
diferenciales ordinarias (EDO) involucra dos tipos de
error.
1) Errores de Truncamiento, o discretizacion, causados
por la naturaleza de
las técnicas
empleadas para aproximar los valores de
y.
2) Errores de Redondeo, que son el resultado del
número limite de cifras significativas que pueden retener
una computadora.
Método de Euler Mejorado
Este método se basa en la misma idea del
método anterior, pero hace un refinamiento en la
aproximación, tomando un promedio entre ciertas
pendientes.
La fórmula es la siguiente:
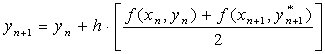
Donde
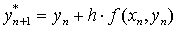
Para entender esta fórmula, analicemos el primer
paso de la aproximación, con base en la siguiente
gráfica:
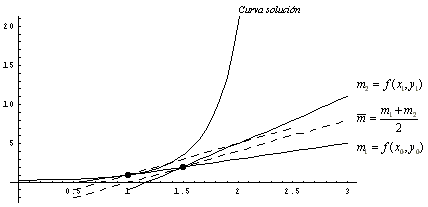
En la gráfica, vemos que la pendiente
promedio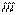 
corresponde a la pendiente de la recta
bisectriz de la recta tangente a la curva en el punto de la
condición inicial y la "recta tangente" a la curva en el
punto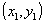 
donde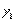 
es la aproximación obtenida con la
primera fórmula de Euler. Finalmente, esta recta bisectriz
se traslada paralelamente hasta el punto de la
condición inicial, y se considera el valor de esta recta
en el punto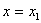 
como la aproximación de Euler
mejorada.
Ayuda del
programa (sintaxis)
Página siguiente  |