Método simplex – Maximización (página 2)

En el algoritmo del
Símplex, se parte de un programa base que
estará formado por vectores
unitarios (vector proceso
unitario), realizando iteraciones sucesivas, de manera que en
cada uno de ellos, la matriz de
coeficientes asociada al programa base sea una matriz identidad.

Los pasos a seguir en el algoritmo del Símplex
son:

1. Convertir desigualdades en igualdades,
introduciendo para ello variables de
holgura, que serán positivas en restricciones menores o
iguales, y negativas en restricciones mayores o
iguales.

2. Obtener el programa base: Esta es la pregunta
inicial de la cual partimos para determinar la solución.
Para encontrar el programa base, tomaremos un vector unitario de
cada una de las restricciones del problema, de acuerdo con el
siguiente esquema:

2.1. Escoger aquellas variables de holgura con el
mismo signo que el término independiente y coeficiente
unitario.

2.2. En su defecto, escoger aquellas variables Xi
que aparezca en una única restricción, y tenga el
mismo signo que el término independiente. Esta variable
deberá tener coeficiente unitario.

2.3. En su defecto, introduciremos en aquellas
restricciones de las cuales no hemos tocado aún, un vector
unitario una variable artificial Kj afectada de un rendimiento
–N si estamos maximizando, o de un rendimiento +N si
estamos minimizando, y que tendrá un coeficiente
unitario.

El método
Simplex básico

El método
Simplex, introducido en su forma original por Spendley; Hext
y Himsworth, en 1962, no se basa en planeamientos factoriales y
por eso requiere pocos experimentos para
moverse, desplazándose en la dirección del óptimo. La
aplicación del método
Simplex en Química
Analítica fue efectuada por la primera vez en 1969. El
método Simplex original, a lo largo de estos años,
há sufrido modificaciones que obligaron a la
distinción del mismo dentro de las estrategias de
optimización, así el método Simplex original
pasó a ser llamado de Método Simplex Básico
(MSB).

El procedimiento de
optimización, en el método Simplex, comienza por la
elección de la n+1 puntos donde será hecha la
evaluación de la respuesta. Este resultado
será evaluado contra las demás respuestas para que
el proceso pueda continuar, siendo que este tipo de desarrollo
convierte al simplex en un método del tipo
secuencial.

El procedimiento es repetido sucesivamente,
descartándose la peor respuesta. Por lo tanto, como vemos,
el objetivo del
método Simplex secuencial es forzar al simplex a moverse
para la región de respuesta óptima.

Las decisiones requeridas para que eso sea posible
constituyen las llamadas "reglas" del procedimiento
simplex.REGLAS PARA EL MOVIMIENTO DEL
SIMPLEX BÁSICO

Regla nº 1: Después de
determinar las respuestas de los n+1 experimentos necesarios para
iniciar el proceso, con base en el
conocimiento ya adquirido sobre el sistema, se debe
clasificarlas en mejor [B (the Best)], peor [W (the Worst)] y
resultados intermediarios [N (Next to worst)], según el
objetivo de la optimización.

Regla nº 2: El simplex es movido para
un simplex adyacente, el cuál es determinado descartando
la respuesta menos deseada. El vértice correspondiente a
esta respuesta es sustituido por un nuevo vértice,
generado por su reflexión a través del centroide de
la hiperfase de los vértices restantes.

Matematicamente, sí los vértices de un
simplex k-dimensional son representados por coordenadas
vectoriales P1, P2, …., Pj, ….Pk, …. Pk+1, la
eliminación de la respuesta no deseada Pj resulta en la
hiperfase formada por P1, P2, …., Pj-1, Pj+1, ….Pk, …. Pk+1
con el centroide definido por:

Pc = 1/k (P1 + P2 + …. + Pj-1 + Pj+1 + …. + Pk +
Pk+1)

Pc = centroide de la hiperfase K =
número de dimensiones del simplexPj = vértice
correspondiente a la peor respuesta.

El nuevo simplex es definido por esta fase y un nuevo
vértice, P, que corresponde a la reflexión del
vértice rechazado Pj, a través de la fase por el
centroide Pc.

P = Pc + (Pc – Pj)

Regla nº 3: Sí el punto
reflejado, P, tuviera la peor respuesta en el nuevo simplex,
probablemente el desplazamiento no está sucediendo en
dirección al óptimo. En este caso, se debe rechazar
la 2ª peor respuesta de este simplex y continuar con la
optimización.

Esta regla es necesaria, pues el simplex puede estar
encima de una cresta y la aplicación directa de la Regla
no 2 puede hacer con que el punto P sea reflejado de vuelta al
punto anterior. En este caso el simplex oscila y se vuelve sin
recurso (decimos, que se mantiene parado).

Esta situación sucede con frecuencia en la
región del óptimo. Sí un punto es obtenido
cercano a él, todos los otros nuevos puntos tienden a
pasar más allá del tope de la curva de respuesta.
Entonces, un cambio en la
dirección es indicado. En la región del
óptimo, normalmente ocurre el simplex circular en vuelta
de un óptimo temporáneo. Como se puede tratar de un
resultado falso, el cual hace, con que el simplex se prenda a
él, es necesario la siguiente excepción adicional a
la Regla no 1.

Regla nº 4: Sí un
vértice fuera mantenido en k+1 simplex, antes de aplicar
la Regla no 2, haga una nueva observación del vértice persistente.
Sí el vértice está realmente cercano al
óptimo, es probable que la evaluación repetida de
la respuesta sea consistente y de esta forma el punto será
mantenido. Sí la respuesta en el vértice fuera alta
por causa de un error de observación, es improbable que
con la nueva evaluación eso ocurra y por lo tanto, el
vértice será consecuentemente eliminado.

Regla nº 5: Sí el nuevo
vértice encontrarse fuera de los limites aceptables de las
variables optimizadas, no se deben realizar observaciones
experimentales con estos valores, al
contrario se debe atribuir a este la respuesta más
indeseable.

La aplicación posterior de las Reglas nos 2 e 3
obligará al simplex a regresar dentro de los límites
permitidos y este continuará buscando por la respuesta
óptima. Cuando un óptimo es localizado, las reglas
del simplex lo fuerzan a circular.

Localización y tamaño del
simplex inicial

En la etapa inicial de los experimentos, es recomendable
construir un simplex grande para que por sí mismo se mueva
rápidamente sobre la superficie de respuestas y pueda
localizar la región del óptimo. Para definir
más precisamente el óptimo, se construye un simplex
menor y se continúa la optimización. En el caso que
sea necesario, es posible repetir el proceso, dejando el simplex
cada vez más pequeño. Está claro que existe
una limitación para el tamaño del simplex, pues,
sí este fuera muy pequeño, los errores
experimentales pueden enmascarar los verdaderos efectos sobre la
respuesta y hacer con que el simplex se traslade irregularmente
dentro de un área cercana al óptimo.

Para definición del primer simplex
se debe establecer las variables que estarán sujetas a la
optimización. Después, se define el tamaño
del paso () de cada variable del simplex. Con el auxilio de la
Tabla 1, se puede construir el simplex inicial hasta con 7
(siete) factores.

Tabla 1: Valores para el tamaño
del paso hasta para 10 factores

Ejemplo: Optimización de las
condiciones de funcionamiento de un cromatógrafo para un
determinado análisis.

Variables:1- Temperatura,
ºC. 2- Velocidad de
flujo del gas de arrastre,
mL/min. 3- Longitud de la columna, cm.

Valores iniciales:Temperatura, T =
20 ºC. Velocidad de flujo del gas de arrastre, V = 40
mL/min. Longitud de la columna, C = 200 cm.

Pasos de las Variables (Step size,
SS):Temperatura => SSt = 10 ºC. Velocidad del flujo
del gas de arrastre => SSv = 5 mL/min. Longitud de la columna
=> SSc = 20 cm.

Los vértices nuevos son obtenidos
sumándose al punto inicial el paso de cada variable
multiplicado por el factor correspondiente de la Tabla 1.
Los experimentos previstos para este ejemplo están
relacionados en la Tabla 2.

Tabla 2: Determinación de los
vértices del simplex inicial

Consideraciones Generales

El método Simplex no requiere el uso de test
estadísticos de significancia por dos razones:

a) sí las diferencias en las respuestas son
grandes al ser comparadas con el error experimental, el simplex
se mueve en la dirección correcta.

b) sí las diferencias son bastante
pequeñas para ser afectadas por el error experimental, el
simplex se mueve en la dirección equivocada. Incluso, un
movimiento en la dirección equivocada provocaría
una respuesta indeseable, que rápidamente
produciría una corrección en la dirección
tomada, a través de las Reglas nos 2 e 3, y el simplex
aunque momentáneamente fuera de curso, volvería
nuevamente en dirección al óptimo.

Se debe llevar en cuenta que el método Simplex no
puede ser utilizado en la determinación de variables
cualitativas, del tipo presencia o no de un determinado factor.
La aplicación de este método también no es
aconsejable caso las condiciones experimentales sean de
difícil control u
obtención, además que sólo es posible
optimizar un factor por vez.

En particular, en el uso del método
simplex básico, tres limitaciones son
evidentes:

Primero: El óptimo solamente
es localizado con precisión por casualidad.

Segundo: Un óptimo falso
puede ser localizado.

Tercero: El progreso del simplex en
dirección al óptimo solamente puede ser efectuado
en una proporción constante.

Estos inconvenientes motivaron la
modificación del método simplex básico,
convirtiéndolo más eficiente en la búsqueda
del óptimo, originando el método simplex modificado
(MSM).

Método Simplex
modificado

En 1965, Nelder y Mead, propusieron modificaciones en el
procedimiento original de movimentación del simplex
básico, que permitió obtener un punto óptimo
estacionario con suficiente precisión y claridad,
además de permitir un desarrollo mas rápido del
simplex en dirección al óptimo, originando el
denominado Método Simplex Modificado (MSM), donde pueden
ser alterados el tamaño y la forma del simplex. Las reglas
de movimiento del método Simplex básico son
válidas y a estas fueron aumentadas, por Nelder y Mead,
otras que caracterizan el MSM, volviéndolo probablemente
el más aplicado en química.

Reglas para el movimiento del simplex
modificado

Las reglas adicionales de movimiento del
Método Simplex Modificado.

Andamiento del Método Simplex Modificado
Considere el simplex inicial representado por B, N y W en la
figura 8. Suponga que W es el vértice que dá la
peor respuesta, B la mejor respuesta y N la segunda peor
respuesta. Así, como en el método simplex
básico, el primer movimiento del simplex modificado es la
reflexión y los vértices para el movimiento del
simplex pueden ser resumidos por la ecuación:

P = Pc + b (Pc – W)

P = vértice para el movimiento del
simplex. Pc= centroide. W= vértice correspondiente a la
peor respuesta.

b = coeficiente de movimiento del simplex.

En el método simplex básico, el
único valor
permitido para el andamiento del simplex es b = 1,
correspondiente a la reflexión, generando el
vértice R. Sin embargo, para el Método Simplex
Modificado otros valores son permitidos y definidos
después de cada observación de la respuesta en
comparación con las respuestas obtenidas en los
vértices originales representados por B, N y W.

Existen cuatro posibilidades con relación a la
respuesta obtenida en R para ser consideradas, las cuáles
generan las siguientes reglas de movimiento del simplex
modificado.

Regla nº 1: Sí la respuesta en
R fuera mejor que la respuesta en B, indica que el simplex
está caminando en la dirección correcta. Se debe
realizar una expansión del simplex inicial.
Haciendo b = 2 se duplica el tamaño del simplex en la
dirección deseada y se realiza el experimento en S.
Sí la respuesta en S fuera mejor que las anteriores, el
nuevo simplex será SBN.

Regla nº 2: Sí la respuesta en
R fuera peor que en W, significa que el simplex además de
no estar caminando en la dirección correcta, está
con tamaño inadecuado. Se debe realizar una
contracción con cambio en la dirección del
simplex RNB, generando el vértice T, para el cual b = –
½. Sí la respuesta en T fuera mejor que en W, el
nuevo simplex será BNT.

Regla nº 3: Sí la respuesta en
R fuera peor que en N, pero mejor que en W, significa que el
simplex está muy grande, pero en la dirección
correcta. Se hace una observación en U (b = ½).
Sí la respuesta en U fuera intermediaria entre B y N, el
nuevo simplex será BUN, ósea, se hace una
contracción.

Regla nº 4: Sí la respuesta en
R fuera intermediaria entre B y N, estas operaciones no
son recomendables y el nuevo simplex será BRN,
procediéndose como en el caso del simplex
básico.

Los movimientos del simplex modificado están
resumidos en la Tabla 3. Los valores de
b, correspondientes a la expansión y contracción
del simplex pueden asumir valores diferentes de los relacionados
en la tabla 3, pero en general estos son los más
usados.

Tabla 3: Movimientos del simplex
modificado

* CMD, contracción con cambio de
dirección

Cuando los recursos
adicionales de movimiento del simplex (MSM) se muestren
equívocos (principalmente la contracción), es
decir, el simplex no se mueve, se recomienda una reducción
del simplex, también llamada de Contracción
Brusca. Es decir, se conserva el vértice B del simplex
y se hacen nuevas observaciones para determinar los otros
vértices nuevos N' y W', determinados de la siguiente
forma:

N' = (B + N) / 2 y W' = (B + W) /
2

La idea, aunque efectiva, sufre dos
desventajas. La primera, que requiere de la evaluación de
los nuevos k vértices del simplex reducido para que el
proceso de optimización pueda continuar (donde k es el
número de factores del procedimiento en
optimización). La segunda, es que el tamaño del
simplex, cada vez que ocurre una contracción brusca, es
reducido y esto puede resultar en la convergencia prematura del
simplex en la presencia del error experimental.

Método Simplex súper
modificado

Existe aún un algoritmo más sofisticado
para la optimización utilizando el método simplex,
el simplex súper modificado. En este método la
forma y el tamaño del simplex pueden ser ajustados de
acuerdo con las características de la superficie
analizada, haciendo la búsqueda por el óptimo
aún más eficiente. Sin embargo, el tratamiento
matemático necesario para su desarrollo se vuelve
más complejo, involucrando el ajuste de ecuaciones
polinomiales, además, siendo necesario realizar un
experimento más a cada movimiento del simplex.

PREPARANDO EL MODELO PARA
ADAPTARLO AL MÉTODO SIMPLEX

Esta es la forma estándar del modelo:

Para ello se deben cumplir las siguientes
condiciones:

• El objetivo es de la forma de
  maximización o de minimización.

• Todas las restricciones son de
  igualdad.

• Todas las variables son no
  negativas.

• Las constantes a la derecha de las
  restricciones son no negativas.

Cambio del tipo de
optimización.

Si en nuestro modelo, deseamos minimizar, podemos
dejarlo tal y como está, pero deberemos tener en cuenta
nuevos criterios para la condición de parada (deberemos
parar de realizar iteraciones cuando en la fila del valor de la
función
objetivo sean todos menores o iguales a 0), así como para
la condición de salida de la fila. Con objeto de no
cambiar criterios, se puede convertir el objetivo de minimizar la
función F por el de maximizar F·(-1).

Ventajas: No deberemos preocuparnos por los
criterios de parada, o condición de salida de filas, ya
que se mantienen.

Inconvenientes: En el caso de que la
función tenga todas sus variables básicas
positivas, y además las restricciones sean de desigualdad
"=", al hacer el cambio se quedan negativas y en la fila del
valor de la función objetivo se quedan positivos, por lo
que se cumple la condición de parada, y por defecto el
valor óptimo que se obtendría es 0.

Solución: En la realidad no existen este
tipo de problemas, ya
que para que la solución quedara por encima de 0, alguna
restricción debería tener la condición "=",
y entonces entraríamos en un modelo para el método
de las Dos Fases.

Conversión de signo de los
términos independientes (las constantes a la derecha de
las restricciones)

Deberemos preparar nuestro modelo de forma que los
términos independientes de las restricciones sean mayores
o iguales a 0, sino no se puede emplear el método Simplex.
Lo único que habría que hacer es multiplicar por
"-1" las restricciones donde los términos independientes
sean menores que 0.

Ventaja: Con ésta simple
modificación de los signos en la
restricción podemos aplicar el método Simplex a
nuestro modelo.

Inconvenientes: Puede resultar que en las
restricciones donde tengamos que modificar los signos de las
constantes, los signos de las desigualdades fueran ("=", "="),
quedando ("=","=") por lo que en cualquier caso deberemos
desarrollar el método de las Dos Fases. Este inconveniente
no es controlable, aunque nos podría beneficiar si
sólo existen términos de desigualdad ("=","="), y
los "=" coincidieran con restricciones donde el término
independiente es negativo.

Todas las restricciones son de igualdad.

Si en nuestro modelo aparece una inecuación con
una desigualdad del tipo "=", deberemos añadir una nueva
variable, llamada variable de exceso si, con la
restricción si = 0. La nueva variable aparece con
coeficiente cero en la función objetivo, y restando en las
inecuaciones.

Surge ahora un problema, veamos como queda una de
nuestras inecuaciones que contenga una desigualdad "=" :

a11·x1 + a12·x2 = b1 a11·x1 +
a12·x2 – 1·xs = b1

Como todo nuestro modelo, está basado en que
todas sus variables sean mayores o iguales que cero, cuando
hagamos la primera iteración con el método Simplex,
las variables básicas no estarán en la base y
tomarán valor cero, y el resto el valor que tengan. En
este caso nuestra variable xs, tras hacer cero a x1 y x2,
tomará el valor -b1. No cumpliría la
condición de no negatividad, por lo que habrá que
añadir una nueva variable, xr, que aparecerá con
coeficiente cero en la función objetivo, y sumando en la
inecuación de la restricción correspondiente.
Quedaría entonces de la siguiente manera:

a11·x1 + a12·x2 = b1 a11·x1 +
a12·x2 – 1·xs + 1 ·xr = b1

Este tipo de variables se les llama variables
artificiales, y aparecerán cuando haya inecuaciones con
desigualdad ("=","="). Esto nos llevará obligadamente a
realizar el método de las Dos Fases, que se
explicará más adelante.

Del mismo modo, si la inecuación tiene una
desigualdad del tipo "=", deberemos añadir una nueva
variable, llamada variable de holgura si, con la
restricción si "=" 0. La nueva variable aparece con
coeficiente cero en la función objetivo, y sumando en las
inecuaciones.

A modo resumen podemos dejar esta tabla, según la
desigualdad que aparezca, y con el valor que deben estar las
nuevas variables.

Desarrollando el
método Simplex

Una vez que hemos estandarizado nuestro modelo, puede
ocurrir que necesitemos aplicar el método Simplex o el
método de las Dos Fases. Véase en la figura como
debemos actuar para llegar a la solución de nuestro
problema.

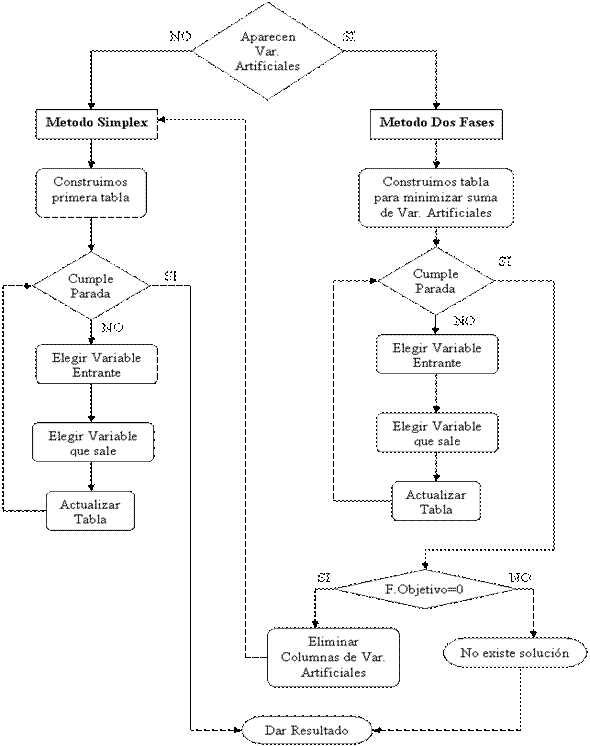
 Explicaremos paso a paso los puntos de cada
método, concretando los aspectos que hay que tener en
cuenta.

• 1. Construcción de la primera
  tabla: En la primera columna de la tabla aparecerá
  lo que llamaremos base, en la segunda el coeficiente que
  tiene en la función objetivo cada variable que aparece
  en la base (llamaremos a esta columna Cb), en la tercera el
  término independiente de cada restricción (P0),
  y a partir de ésta columna aparecerán cada una
  de las variables de la función objetivo (Pi). Para
  tener una visión más clara de la tabla,
  incluiremos una fila en la que pondremos cada uno de los
  nombres de las columnas. Sobre ésta tabla que tenemos
  incluiremos dos nuevas filas: una que será la que
  liderará la tabla donde aparecerán las
  constantes de los coeficientes de la función objetivo,
  y otra que será la última fila, donde
  tomará valor la función objetivo. Nuestra tabla
  final tendrá tantas filas como
  restricciones.

Los valores de la fila Z se obtienen de la siguiente
forma: El valor Z0 será el de sustituir Cim en la
función objetivo (y cero si no aparece en la base). El
resto de columnas se obtiene restando a este valor el del
coeficiente que aparece en la primera fila de la
tabla.

Se observará al realizar el método
Simplex, que en esta primera tabla, en la base estarán las
variables de holgura.

• 2. Condición de parada:
  Comprobaremos si debemos de dar una nueva iteración o
  no, que lo sabremos si en la fila Z aparece algún
  valor negativo. Si no aparece ninguno, es que hemos llegado a
  la solución óptima del problema.

• 3. Elección de la variable que
  entra: Si no se ha dado la condición de parada,
  debemos seleccionar una variable para que entre en la base en
  la siguiente tabla. Para ello nos fijamos en los valores
  estrictamente negativos de la fila Z, y el menor de ellos
  será el que nos de la variable entrante.

• 4. Elección de la variable que
  sale: Una vez obtenida la variable entrante, obtendremos
  la variable que sale, sin más que seleccionar aquella
  fila cuyo cociente P0/Pj sea estrictamente positivo (teniendo
  en cuenta que sólo se hará cuando Pj sea mayor
  de 0). La intersección entre la columna entrante y la
  fila saliente nos determinará el elemento
  pivote.

• 5. Actualización de la tabla: Las
  filas correspondientes a la función objetivo y a los
  títulos permanecerán inalterados en la nueva
  tabla. El resto deberá calcularse de dos formas
  diferentes:

• Si es la fila pivote cada nuevo
  elemento se calculará:Nuevo Elemento Fila Pivote =
  Elemento Fila Pivote actual / Pivote.

• Para el resto de elementos de filas se
  calculará:Nuevo Elemento Fila = Elemento Fila Pivote
  actual – (Elemento Columna Pivote en la fila actual * Nuevo
  Elemento Fila).

Interpretación gráfica del
Método Simplex

La resolución de problemas lineales con
sólo dos o tres variables de decisión se puede
ilustrar gráficamente, mostrándose como una ayuda
visual para comprender muchos de los conceptos y términos
que se utilizan y formalizan con métodos de
solución más sofisticados, como por ejemplo el
Método Simplex, necesarios para la resolución de
problemas con varias variables. Para ello se puede usar el
método Gráfico.

Aunque en la realidad rara vez surgen problemas con
sólo dos o tres variables de decisión, es sin
embargo muy útil esta metodología de solución e interpretación, en la que se verán
las situaciones típicas que se pueden dar, como son la
existencia de una solución óptima única, de
soluciones
óptimas alternativas, la no existencia de solución
y la no acotación. Describimos aquí las fases del
procedimiento de solución del Método
Gráfico:

• Dibujar un sistema de coordenadas cartesianas en el
  que cada variable de decisión esté representada
  por un eje, con la escala de medida adecuada a su variable
  asociada.

• Dibujar en el sistema de coordenadas las
  restricciones del problema (incluyendo las de no
  negatividad). Para ello, observamos que si una
  restricción es una inecuación, define una
  región que será el semiplano limitado por la
  línea recta que se tiene al considerar la
  restricción como una igualdad. Si la
  restricción fuera una ecuación, la
  región que define se dibuja como una línea
  recta. La intersección de todas las regiones determina
  la región factible o espacio de soluciones (que es un
  conjunto convexo). Si esta región es no vacía,
  ir a la fase siguiente. En otro caso, no existe
  solución que satisfaga (simultáneamente) todas
  las restricciones y el problema no tiene solución,
  denominándose infactible o no factible.

• Determinar los puntos extremos (puntos que no
  están situados en segmentos de línea que unen
  otros dos puntos del conjunto convexo) de la región
  factible (que, como probaremos en la siguiente
  sección, son los candidatos a solución
  óptima). Evaluar la función objetivo en estos
  puntos y aquél o aquellos que maximicen (o minimicen)
  el objetivo, corresponden a las soluciones óptimas del
  problema.

Problemas
propuestos

• 1. Las restricciones pesqueras impuestas por la
  CEE obligan a cierta empresa a pescar como máximo
  2.000 toneladas de merluza y 2.000 toneladas de rape,
  además, en total, las capturas de estas dos especies
  no pueden pasar de las 3.000 toneladas. Si el precio de la
  merluza es de 1.000 ptas/kg y el precio del rape es de 1.500
  ptas/kg, ¿qué cantidades debe pescar para
  obtener el máximo beneficio?

• 2. Una compañía manufacturera
  puede producir dos productos A y B. La
  producción esta organizada en tres departamentos:
  fabricación, ensamble y pintura, con capacidades
  semanales de 72 hora, 30 horas y 40 horas para los tres
  departamentos, respectivamente. Cada unidad del producto
  A requiere dos horas de tiempo de fabricación,
  una hora de ensamble y dos horas de pintura. Las condiciones
  en las ganancias son de $ 8 y $ 10 por unidad del producto
  A y B, respectivamente. La
  compañía es capaz de vender cualquier cantidad
  de los dos productos, determine:

• a) La solución optima, empleando el
  método simplex (maximización).

• 3. La Compañía HBB fabrica 4
  productos que requieren para su elaboración, de
  materia prima con una disponibilidad diaria de 180 libras, un
  espacio total disponible para almacenamiento de 230 pies
  cuadrados y en producción se utilizan 5 horas diarias.
  Para elaborar una cantidad de cada uno de los productos se
  requieren los siguientes insumos:

¿Cuántas unidades de cada producto deben
fabricarse para maximizar el beneficio?

EJERCICIOS

• 1. Cierta empresa química produce dos
  tipos de disolventes (D1 y D2). La producción de estos
  disolventes se lleva a cabo en dos plantas: Una de mezclado y
  otra de purificación. La capacidad semanal de horas de
  trabajo es de 230 h. para mezclado y 250 horas para
  purificación (son horas semanales). Para la
  fabricación de 1 litro de ambos tipos, son necesarias
  las siguientes horas:

Esta empresa tiene una
provisión casi ilimitada de materiales,
sin embargo, se conoce que el disolvente D2 tiene una demanda
semanal nunca superior a 120 litros. Determinar el plan de
fabricación semanal máximo para la empresa si el
beneficio del disolvente D1 es de $300 y de D2 de $500 por litro
cada uno.

• 2. Una mueblería fabrica escritorios,
  mesas y sillas. La fabricación requiere de materia
  prima y de mano de obra. La mano de obra se clasifica en dos
  tipos: carpintería y terminaciones. La cantidad de
  recurso requerido para cada tipo de producto se muestra en la
  siguiente tabla:

Actualmente se dispone de 48 pulgadas madereras, 20
horas para terminaciones y 8 horas para carpintería. Cada
escritorio se vende a $ 60, cada mesa a $ 30 y cada silla a $ 20.
La empresa piensa que la demanda por escritorios y sillas es
ilimitada, pero cree que se venderán a lo más 5
mesas. Debido a que los recursos ya han sido adquiridos, la
empresa desea maximizar su beneficio.

• 3. Una fábrica produce dos modelos A y B
  de un producto. El beneficio que arroja el modelo A es de
  $4000 por unidad y el del B $6000 por unidad. La
  producción diaria no puede superar 400 unidades del
  modelo A ni 300 del B y en total no pueden superarse las 600
  unidades. ¿Cuántas unidades de cada modelo debe
  producir la fábrica para obtener el máximo
  beneficio?

• 4. Un automóvil puede transportar como
  máximo 9 Kilogramos por viaje. En un viaje desea
  transportar al menos 5 Kilogramos de la mercancía A y
  un peso de la mercancía B que sea la mitad del peso
  que transporta de A. Sabiendo que cobra $30 por kilo de A y
  $20 por kilo de B, ¿cómo se debe cargar el
  camión para obtener la ganancia
  máxima?

• 5. Usted, como vendedor de FERRETERIA C.A.
  tiene que decidir cómo asignar sus esfuerzos entre los
  diferentes tipos de clientes de su territorio. Usted debe
  visitar comerciantes mayoristas y clientes que compran al
  detal. Una visita a un comerciante mayorista usualmente le
  produce $20 en ventas, pero la visita en promedio dura 2
  horas y debe manejar también en promedio 10 Km. En una
  visita a un comprador al detal, le vende $50  requiere
  de unas 3 horas y 20 Km manejando su carro aproximadamente.
  Usted planifica viajar como máximo 600 Km por semana
  en su carro y prefiere trabajar no más de 36 horas a
  la semana. Encuentre la combinación óptima de
  visitas a comerciantes y clientes al menudeo que le permitan
  maximizar sus ganancias

Autor:

Bernard Pavel Barreto
Véliz