Introducción
Cuando nos referimos a las cónicas, usualmente
pensamos solo en la parte matemática, vale decir, las
ecuaciones y los conceptos de éstas. Sin embargo, desde
los tiempos antiguos tenían utilidades prácticas
(ya sea medio legendarios como la hazaña de
Arquímedes, al destruir naves romanas con un espejo
gigante o reales, como la creación de espejos
pequeños, importantes más adelante en la
óptica)
En la Edad Moderna y Contemporánea, adquirieron
mayor relevancia para el ser humano en ámbitos tanto
matemáticos como físicos, inclusive llegando
más allá, sobrepasando las expectativas que se
tenían, como el uso en telecomunicaciones e
industria.
Quizá, cuando la tecnología siga avanzando
tal como lo hace ahora en el siglo XXI, tendremos que recurrir a
las ideas de las cónicas, con propósito de mejorar
lo preexistente.
Cónicas y
Aplicaciones
Para poder hablar en si sobre las cónicas,
debemos remontarnos a la Antigua Grecia, sobre los años
350 A.C con el descubrimiento de éstas por parte del
matemático griego Menecmo y la descripción
detallada por parte del matemático Apolonio (262-190 A.C.)
de Perga, quien estudió las propiedades de las curvas
cónicas.
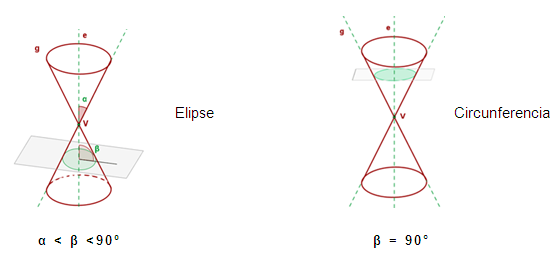
SECCION CONICA: También conocida como
curva cónica, está engendrada por el giro de una
recta g, generatriz (recta situada en el cono), alrededor de otra
recta e, eje, con el cual se corta en un punto V, vértice
a la curva intersección de un cono con un plano que no
pasa por este. En función de la relación existente
entre el ángulo de conicidad (a) y la inclinación
del plano respecto del eje del cono (ß), pueden obtenerse
diferentes secciones cónicas.

Asimismo, Apolonio, proveniente de la escuela
alejandrina y guiado por el sabio Arquímedes, clasifico
las secciones cónicas en tres tipos:
Elipses.
Hipérbolas.
Parábolas.
ELIPSES: Proviene del término
elipsis, que significa una deficiencia, se utilizaba
cuando un rectángulo dado debía aplicarse a un
segmento dado y resultaba escaso en un cuadrado (u otra figura
dada).
Su definición actual señala que la elipse
es el conjunto de puntos en un plano, tales que la suma de sus
distancias desde dos puntos fijos es constante, denominando
foco al punto fijo. Se obtienen a partir de una
sección cónica si el plano cortante no es paralelo
a ninguna generatriz, además, existe un caso especial
denominado circunferencia, la cual se forma si el plano
cortante interseca a cada generatriz y también es
perpendicular al eje del cono.
Tenemos primero el punto T(x, y), siendo cualquier punto
de la elipse si y sólo si: Recta TF + Recta TF`=
2a.

HIPERBOLAS: En el griego antiguo significaba
"avanzar más allá", se adoptó en
términos de las cónicas para el caso en que el
área excedía el segmento dado.
Actualmente se le denomina hipérbola al conjunto
de puntos en un plano, tales que el valor absoluto de la
diferencia de sus distancias a dos puntos fijos es una constante,
los cuales se llaman focos. Se obtiene cuando un plano
cortante interseca los dos mantos de un cono y es paralelo a dos
generatrices.
La recta que une los dos focos se llama eje real de la
hipérbola y la mediatriz se llama eje imaginario de la
hipérbola. El punto donde se cortan ambos ejes (que es el
punto medio de los focos) se llama centro de la
hipérbola.

PARABOLAS: La palabra parábola en los
tiempos de Apolonio tenía como significado "colocar al
lado" o "comparar" indicando que no había ni deficiencia
ni exceso.
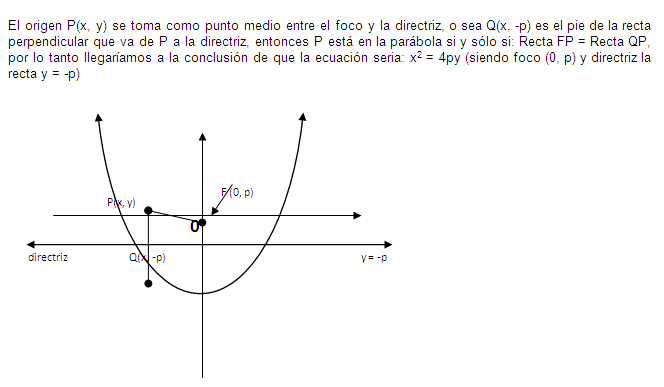
Su definición actual afirma que es el conjunto de
todos los puntos situados en un plano que equidistan de un punto
y una recta fijos. El punto fijo se denomina foco y la
recta fija, directriz.
La distancia entre el foco y la directriz de una
parábola recibe el nombre de parámetro de la
parábola (suele denotarse por p). Dada una
parábola, se llama eje de la misma la recta que contiene
al foco y es perpendicular a la directriz. Se llama
vértice de la parábola al punto donde ésta
corta a su eje.
A partir de la definición, podemos derivar la
ecuación de una parábola. Para ello, se elige el
eje y como recta perpendicular, la directriz, conteniendo
así el foco.
Aplicaciones
Historia y aplicaciones generales: Desde la
época en que Apolonio demostraba las propiedades que
poseen las curvas cónicas, descubrió que se
destacaba la creación de espejos con forma de
sección cónica aplicando las propiedades de
reflexión, obteniendo así los llamados espejos
elípticos, parabólicos o
hiperbólicos.
Página siguiente  |
