Este capítulo comprende diversas propiedades
geométricas de secciones (para casos prácticos,
secciones de vigas) siendo la más importante el momento de
inercia. Entre otras propiedades estudiadas están los
conceptos de centroide, radio de giro y el teorema de Steiner o
de los ejes paralelos.
3.1
CENTROIDE
Antes de poder empezar a definir el concepto de momento
de inercia es necesario entender completamente lo que es un
centroide y cómo se obtiene. El centroide de un
área se refiere al punto que define el centro
geométrico del área.
El enfoque dado al estudio del centroide es ejemplificar
cómo se obtiene el centroide de una sección
compuesta por diferentes áreas geométricas. Puesto
que el concepto básico no necesita gran atención
por su simplicidad, se empieza por resolver un ejemplo de una
sección compuesta.
Para fines prácticos, el paquete estudia una
sección transversal que se obtiene de una viga cargada
mediante una animación (Figura 3.1 y 3.2). Esto para
captar la atención del usuario y vea alguna de las
aplicaciones inmediatas del concepto.

Figura 3.1 Viga

F igu r a 3.2 Sección transversal de
viga
Obtenida la sección, se divide en áreas
sencillas, manejando diferentes colores para cada una y
así poder distinguirlas fácilmente. A
continuación se presentan las dimensiones de cada
área, cada dato de un color diferente, lo cual será
de ayuda posteriormente (Figura 3.3).

Figur a 3.3 División de la
sección
Se le da la opción al usuario de elegir
qué respecto a que eje desea obtener el centroide. Una vez
que este selecciona una opción aparece el eje de
referencia necesario. También se presentan la distancia de
los centroides de cada área individual hacia el eje
(Figura 3.4).

F igu r a 3.4 Punto de
decisión
Aparece la demostración de la
fórmula de centroide de áreas
compuestas:

Los momentos estáticos del área total del
eje x/y deberán ser igual a la sumatoria de momentos
estáticos de las áreas parciales respecto al mismo
eje. Seguido de esto se visualiza la expresión necesaria
para obtener el centroide deseado.
Al aplicar la expresión del centroide en el
paquete se observa cómo los datos son arrastrados desde la
figura de la sección transversal hasta la fórmula.
Con ayuda de los colores el usuario puede ubicar de dónde
proviene cada dato y así comprenderá más
rápido cómo debe usarse la expresión (Figura
3.5).
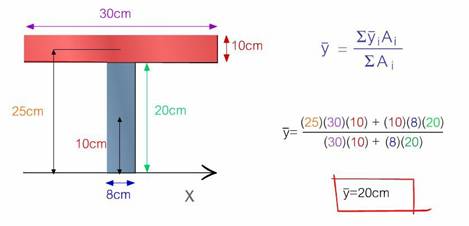
Figur a 3.5 Obtención la coordenada
y del centroide
Terminada la obtención de un centroide, el
usuario vuelve a encontrar la opción para decidir si desea
ver el ejemplo del centroide respecto al otro eje o seguir a otro
tema.
3.2 MOMENTO DE
INERCIA
La integral  representa el momento de inercia respecto al
representa el momento de inercia respecto al
eje x. Popov dice:
" La integral depende sólo de las propiedades
geométricas del área transversal. En
mecánica esta cantidad lleva el nombre de momento de
inercia (o momento de segundo orden) del área de la
sección respecto al eje centroidal, cuando y se mide desde
tal eje. Es una constante definida para la forma del área
en particular y se designa por I " (1982).
El paquete trata de la manera más práctica
posible el concepto de momento de inercia, puesto que es una
propiedad geométrica y sin ninguna representación
física
Para iniciar se toma la sección transversal de
una viga y en ella se definen dA y y (Figura
3.6). Posteriormente, al momento de realizar la
integral, el área de la viga se va fraccionando, lo que
representa los diferentes dA que forman parte de la integral
(Figura
3.7), para cada uno de estos, dA implica una "y" nueva.
Como ayuda visual al realizar la
integral, las expresiones de Ix e Iy se van "llenando"
de tinta roja, expresando que hasta que se tomen en cuenta todos
los dA el Ix estará completo. Al mismo tiempo, la
sección de la viga se va tornando roja (Figura
3.8).

Figur a 3.6Variables que participan en la
integral


Figu r a 3.7 Se presentan todos los dA
que se pueden encontrar en el área.

Figur a 3.8 Al momento de
integrar
Como es sabido, estas integrales ya han sido resueltas
para las figuras con geometría básica:
rectángulo, círculo, triángulo. Estas
expresiones quedan expresadas en función de variables que
representan las dimensiones del elemento. En la vida real la
aplicación de estas fórmulas resulta ser la manera
más práctica de obtener los momentos de
inercia.
Por lo tanto, estas fórmulas se le presentan al
usuario en un pequeño menú sencillo donde
tendrá que escoger entre la figura que desee saber su
fórmula (Figura 3.9), una vez seleccionada, aparece la
fórmula (Figura 3.10) y puede regresar al pequeño
menú para elegir otra figura o continuar a otro
tema

F igu r a 3.9 Menú de momento de
inercia de figuras básicas

Figur a 3.10 Momento de inercia para un
círculo
3.3 RADIO DE
GIRO
El radio de giro de un área respecto
al eje x se define como la cantidad rx que satisface la
relación:
Ix= r2x A
En el paquete se empieza la
explicación con una viga sometida a cargas y la
definición anterior de radio de giro. Se prosigue
realizando una ampliación a la sección transversal.
Se definen el Área y el Momento de Inercia (la integral
 y en ese instante
y en ese instante
ya se cuenta con los elementos participantes en la
expresión de Radio de Giro (Figura 3.11).

Figu r a 3.11 Sección a la que se
le encontrará el radio de giro
El propósito del paquete
didáctico es representar visualmente lo que la
expresión significa. Según la ecuación, el
radio de giro representa la distancia en que se concentra toda el
área para que se cumpla la expresión 
Entonces se presenta una animación que parte de
la sección transversal con su centroide y el área
es transportada hacia una nueva ubicación (Figura 3.12);
en este momento es cuando el área se transforma en un
pequeño círculo, representando la
concentración del área en un punto. Enseguida se
muestra la cota de rx que es la distancia necesaria para que se
cumpla la
expresión Ix= r2x A (Figura 3.13).

Figur a 3.12 El área cambiará
de ubicación a una distancia r

Figur a 3.13 El área es
concentrada en un punto a una distancia r del eje
3.4 TEOREMA DE
LOS EJES DE PARALELOS O DE STEINER
Como se sabe, si se conoce el momento de inercia de un
área respecto al eje de inercia centroidal, su momento de
inercia puede determinarse respecto a un eje paralelo usando el
teorema de los ejes paralelos o de Steiner.
La primera escena se enfoca en la demostración
del teorema de Steiner y cómo se utiliza el concepto de
los ejes paralelos. Para ello se presenta una sección con
su área, su eje centroidal, y al lado la fórmula de
Ix (Figura 3.14).

Figur a 3.14 Momento de inercia respecto
al eje centroidal
A continuación se le explica al usuario que se
obtendrá ese mismo momento de inercia pero ahora desde
otro eje paralelo al original (el centroidal) (Figura 3.15). Una
vez presentado el nuevo eje, aparecen las cotas desde éste
hasta los puntos necesarios de la fórmula de Ix (distancia
desde el eje al centroide y desde el centroide del área
hasta dA) (Figura 3.16).

Figura 3.15 Nuevo eje sobre el cual se
obtendrá el momento de inercia

Figu r a 3.16 Elementos necesarios para
el teorema de Steiner
Partiendo de la integral original de
momento de inercia, se guía al usuario paso a paso en la
sustitución de los nuevos valores hasta llegar a la nueva
expresión del "Teorema de ejes paralelos".
Ix´= Ix + Ad2
Terminando la explicación de la
determinación de la fórmula, el usuario puede
continuar a un ejemplo de áreas compuestas para que se
comprenda la aplicación de la expresión.
La sección empleada en el ejemplo es la misma
utilizada para el concepto de centroide, ya que el usuario
está familiarizado con esta sección y conoce su
centroide (Figura 3.17). De igual manera que en el ejemplo
anterior, se le da al usuario la opción de elegir el
Momento de Inercia respecto al eje que él decida (Figura
3.18). Puesto que la sección es una viga T
simétrica respecto al eje y, los cálculos de Ix son
mucho más extensos que los de Iy.

F igu r a 3.17 Sección transversal
con la ubicación de sus centroide

Figur a 3.18 Punto de
decisión
Al elegir "momento de inercia en x" , se traza un nuevo
eje x en el centroide de la sección total, así como
las distancias de éste hasta el centroide de las figuras
individuales (Figura
3.19).

F igur a 3.19 Distancias desde el eje
centroidal x hasta el centroide de cada área
Aparece la fórmula del teorema de Steiner y se
calculan los Ix de cada área individual con ayuda de la
expresión de bh3/12, ya que las secciones son
rectangulares. Con una animación se llevan los datos desde
la figura hasta la fórmula, para que el usuario pueda
entender de
dónde surge cada valor.
Para el Iy es más sencillo pues el eje centroidal
de toda la figura coincide con todos los centroides de las
figuras individuales (Figura 3.20). Entonces se explica que se
debe cancelar el término de Ad2 de la expresión,
quedando la sumatoria de los momentos de inercia de las secciones
individuales (Figura 3.21).

Figur a 3.20 Eje centroidal en y

Figur a 3.21 Reducción de la
fórmula de ejes paralelos para Iy para el
ejemplo
Autor:
Ariel Velázquez
Gutiérrez
