Cuaderno de trabajo número II –
Monografias.com
Cuaderno de trabajo número
II
Números primos
Dado los números naturales
1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,………
Tomemos los dos primeros números y multipliquemos
1×2=2; el resultado significa que organizaremos los
números en dos columnas, por lo tanto, tendremos ahora los
números naturales vistos como se muestra en la tabla
N° 1. Para cualquiera de las dos funciones:
f(m)= 2m + 1 o f(m)= 2m + 2
f(m + 1) – f(m) = 2; entendiendo este valor como
un periodo y haciendo la equivalencia en grados, obtenemos los
datos de la TABLA 2. En la figura 1, visualizados dos vectores de
mismo módulo pero de sentido contrario. Dando como
resultado cero.

El beneficio de este primer paso, si se quiere, es que
la ecuación f(m)=2m+2; representa el conjunto de los
números pares y encabezados por el número primo dos
(2), al eliminar esta columna, queda el conjunto de los
números impares representado por la ecuación f(m)=
2m+1 y por lo tanto, un solo vector F1 con un argumento de
180° o p.
Ahora, multipliquemos los números 1x2x3=6;
entendiendo que el resultado nos obliga a organizar los
números en columnas con la única condición
de que ningún número ubicado en la cabeza de la
columna debe ser mayor a seis (6). Dicho esto, visualizaremos los
números organizados como se indica en la tabla N°
3.

Representando los resultados en su equivalente en
grados, observamos la figura 2, donde se muestran tres vectores
de módulo M con 120° entre ellos. Al eliminar la
columna dos, que representa la función f(m)= 6m + 3; los
números impares múltiplos de tres, el vector
resultante es de módulo M con un argumento de cero grados
(0°). Siguiendo nuestro método, al eliminar la columna
dos, tenemos la columna f(m)= 6m+1 y f(m)= 6m+5. Multipliquemos
los números 1x2x3x5= 30; no se utiliza el número
cuatro (4), debido a que no es un número primo. Se toma
cada columna por separado y se organiza como los casos
anteriores. Recordemos que en la primera fila no puede haber un
valor mayor a treinta (30). Veamos la TABLA 5-A y 5-B:

Al representar la tabla N° 5 en grados, notamos diez
vectores que su sumatoria es 0 +0i; como se puede apreciar en la
figura N° 4, nótese la simetría respecto a la
línea horizontal. Al eliminar las columnas que son
múltiplo de cinco, eliminamos del diagrama los vectores de
F60 y F300, resultando la figura 5.

Unificando las tablas 5-A y 5-B, eliminando las columnas
encabezadas los números cinco (5) y veinticinco (25) y
ordenamos los números llegamos a la TABLA 6.

Para tener clara la idea de lo que hemos hecho hasta
este momento, resumimos:
Se ha propuesto un método en que ordenamos
los números naturales en columnas y que todos los
números de esa columna son múltiplos de un
número primo. Entendiendo que dicho número
primo es el último utilizado para cambiar el periodo
de la función. Ejemplo:
1×2; último número dos (2); periodo
igual a dos (2), se elimina la columna encabezada por este
número.1x2x3; último número tres (3), periodo
igual a seis (6); se elimina la columna encabezada por el
número tres.1x2x3x5; último número cinco (5),
periodo treinta (30); se elimina las columnas encabezadas por
cinco (5) o múltiplos de cinco (5), para este caso
veinticinco (25).Hasta el momento se han alternado el argumento del
vector resultante, así: 180°, 0°,
180°.
Hasta el momento, hemos contado con la suerte de que los
números equivalentes en grados han sido enteros, veamos
qué ocurre si utilizamos el número siete (7); el
nuevo periodo será igual a 1x2x3x5x7= 210. Se organiza
cada columna de la tabla N° 6 en ocho tablas de siete
columnas, dando como resultado cincuenta y seis columnas en ocho
tablas.


Organizamos todos los números que encabezan cada
columna y buscamos su equivalencia en grados, tal como se indica
en la tabla N° 7. En la columna tres, se agregó para
hacer evidente la simetría con respecto al eje horizontal.
En la columna REAL + IMAGINARIO (TODOS), se encuentra la parte
real e imaginaria de todos los vectores. Como en los casos
anteriores la suma es cero. En la última columna se
encuentran eliminados las columnas múltiplo de siete (7);
dando como resultado un vector resultante de módulo M y
argumento de 0°. Manteniendo la consistencia en alternar el
argumento.


Hasta el periodo T=30, el equivalente de los
números en grados fueron números enteros; para un
periodo T=210, como se observa en la tabla N°7, la
mayoría de los ángulos no son enteros. El
próximo periodo es 1x2x3x5x7x11= 2310, como la
conversión a grados pasa necesariamente por una
división entre T y siendo T mayor a 360°, sin duda se
mantendrá esta tendencia. Por esta razón
retomaremos el análisis para T=30.
Para ayudarnos a visualizar lo que ocurre con estos
resultados, representaremos la ecuación f(m)= 30m + a,
como una función continua, pero no podemos olvidar que los
números naturales son enteros y no están definidos
los decimales. Por lo tanto, cualquier valor entre 1 y 2, por
ejemplo, no está definido. Haremos un cambio de variable,
representaremos la función bajo la forma f(x)= seno(?x
– ß); donde ?=2p/T. Para hacer coincidir cada cruce
por cero con un valor de f(m)=30m + a, se toma el periodo como
2T.
En la gráfica N° 1, se observa claramente,
las ocho familias de curvas; nótese que en la
década del diez al diecinueve hay cuatro cruces por cero,
estos cuatro cruces por cero se repiten en la misma familia de
curvas en la década de los cuarenta, en la década
de los setenta, etc.

Dos números primos son gemelos cuando la
diferencia entre ellos es dos (2). Por ejemplo: 13 – 11 =
2, entonces para mejorar nuestra comprensión sobre la
tabla N° 6, es menester que visualicemos:
f1(m+1) – f29(m) = 2 f13(m) – f11(m) = 2
f19(m) – f17(m) = 2
Este resultado no depende si los números son
primos o no, de las ocho familias de curvas sólo tres
pares cumplen tal condición. Para evitar el término
(m+1) en la función f1, sólo debemos caer en cuenta
que f31(m) = f1(m+1); así podemos establecer que f31(m)
– f29(m) = 2
Muy bien, existen tres series o familias donde existen
números primos gemelos.
Serie A: f13(m) y f11(m) Serie B: f19(m) y f17(m) Serie
C: f31(m) y f29(m)
Luego, veremos la tabla N° 6 reformulada en la tabla
N° 8
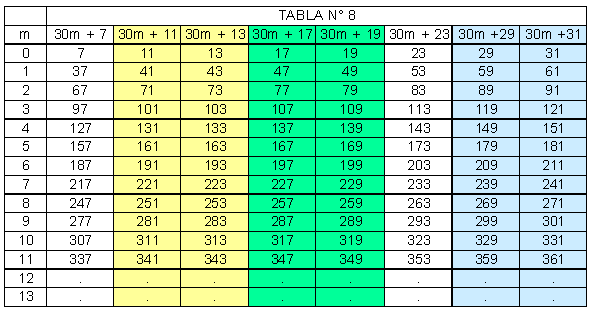
La serie A y B de números primos gemelos, se
encuentra en la misma década y la serie C ésta
conforma con la familia f29, final de década siguiente y
con la familia f31, al inicio de la otra o última
década.
Los números primos de Fermat están
definidos como:

Los números primos tres (3) y cinco (5); no
pertenecen a la familia f(30m + 17), dado que el valor de m no es
un entero positivo.
Los números primos de Mersenne están
definidos como:

En la tabla N° 10, se muestra la correspondencia
entre Números de Mersenne conocidos con las familias f1(m)
y f7(m)

No se pudo realizar la verificación de todos los
números conocidos dado su tamaño.
De las ocho series o familias, sólo la familia
f23(m) no se ha podido relacionar con nada de interés,
circunstancia que la hace muy atractiva para nuevas
investigaciones y publicaciones futuras. Por el momento
respetaremos su discreción.
La gráfica 1 y la figura N°6, pretenden
ubicar toda esta información en un solo plano, la
gráfica 1 pretende visualizar las tres series A, B, y C
donde se encuentran números primos gemelos y en la figura
N° 6 se indica o se asocia números primos especiales a
familias fn(m) específicas.



El vector resultante resulta ser de Módulo: M y
un ángulo de 180°. No debemos olvidar que nuestra
variable de estudio es el ángulo, en otras palabras, los
ocho números primos que son cabeza de serie, están
relacionados con p. Adicionalmente, resulta muy curioso que
cuando se realiza un análisis similar incluyendo los
números primos 2, 3 y 5; el argumento del vector
resultante es un valor muy cercano al radian. ß =
56.69115°.

Este resultado, motivó a analizar en detalla el
resultado para cada combinación de los once elementos o
números primos de la tabla 12. El número de
combinaciones de esas once variables es de dos mil cuarenta y
ocho. N° de combinaciones = 211
Se organizó la información como se muestra
en la tabla 13, que por motivos de espacio no se muestra
completa, recordemos son dos mil cuarenta y ocho
combinaciones.

El cero (0), se interpreta que el vector F13 no esta
tomado en cuenta para la suma, o sea, el número resultante
no es un numero primo. El uno (1) representa un número
primo. En otras palabras f1(m)=30m+ 1 es un número
primo.

IMPORTANTE
Durante todos los cálculos se trató de
mantener, en lo posible, la consistencia tanto en la forma de
realizar los cálculos, así como la nomenclatura.
Esta situación introduce un error que genera la hoja de
cálculo en Excel y lo muestro a
continuación.

Esto se puede notar claramente, viendo la parte real de
los dos casos de la tabla 16.
Cos(12) = Cos(-12) = 0.978147600733806
Cos(60) = Cos(-60) = 0.499999999999998
Pero
Cos(60) ? Cos(300)
Entendiendo que -360° + 300° =
-60°
Esta diferencia genera valores muy pequeñitos del
orden de 10-15 que no hacen visible la simetría con
respecto al eje horizontal, por lo que hay que ser cuidadosos con
su lectura.
Hasta la próxima publicación.
Agradezco sus comentarios a la dirección de
correo
Autor:
José Mujica
Caracas, 04 de Mayo de 2013
