 Página anterior | Voltar ao início do trabalho | Página seguinte  |
Objectivos específicos
Verificar se os alunos aprendem equações equivalentes e como resolvem as equações irracionais.
Diagnosticar o material (livros e planos de aula) que os professores usam ao administrar as suas aulas.
Fazer o estudo bibliográfico sobre equações equivalentes e procedimentos de resolução de equações irracionais.
Capacitar e habilitar os alunos da 12ª classe do PUNIV Joaquim Capango – Huambo nas equações equivalentes e na exercitação de equações irracionais.
Questões de investigação
De acordo os objectivos formulados e para eficientemente dar a resposta ao problema científico diagnosticado, formulou – se as seguintes questões cientificas:
1. Qual é o nível de conhecimento básico sobre equações equivalentes e equações irracionais que os alunos possuem?
2. Que métodos aplicam na resolução de equações irracionais?
3. Que habilidades e capacidades possuem os alunos na resolução de equações irracionais?
4. Quais são as dificuldades que os alunos enfrentam na resolução de equações irracionais?
Tarefas científicas
a) Analisar o nível de conhecimento básico dos alunos no que concerne a equivalência e a irracionalidade.
b) Apresentar métodos eficazes para facilitar a resolução de equações irracionais.
c) Dar aos professores um instrumento de consulta que lhes permitirá atingir com eficácia os objectivos pretendidos.
Hipótese Científica
Em função a criação de exercícios de equações equivalentes e apresentação de métodos de resolução de equações irracionais pode – se contribuir para o pensamento criativo e superar as dificuldades dos alunos da 12ª classe do PUNIV Joaquim Capango – Huambo na exercitação e resolução de outros exercícios no vasto campo das equações.
Métodos de investigação
Métodos teóricos
- Indutivo e dedutivo
- Analise e Síntese
Métodos Práticos
- Observação
- Inquérito
- Estatístico
Significação teórico – prática
Concede – se o conceito de equações, particularizando as equações equivalente e irracionais, as modalidades em que as equações irracionais se apresentam, o seu grau de dificuldade mostrando os métodos de resolução das equações irracionais.
Os exercícios resolvidos, os exemplos apresentados esclarecendo evidentemente as equações equivalentes e a resolução de equações irracionais, assim como a interpretação de exercícios, constitui um material de consulta para os estudantes e docentes de diversas Instituições de Ensino Médio.
Capitulo I
1 – Conceitos básicos
Para todos os efeitos, neste capítulo abordaremos em primeira instância duma forma geral sobre equações, salientando as equações irracionais as quais é o tema a desenvolver, as possíveis transformações que podem acontecer no decurso da sua resolução, em seguida apresentam – se uma série de exemplos ilustrativos para facilitar a compreensão do caro leitor (Professor ou aluno) e tratando de elementos preponderantes para que se resolva uma dada equação.
Para se dar o conceito de equação devemos em primeiro lugar ter a noção de comparabilidade, isto é, saber comparar objectos, e tantas outras coisas como por exemplo comparar duas funções de modo que sejam iguais e representadas pelo sinal de igualdade. Na generalidade e duma forma mais básica diz - se que equação é toda igualdade que contem variável. Mas devemos salientar que estas variáveis não têm dependência, quando tem dependência uma da outra já é um outro aspecto a ser tratado que não foge da regra de função. Por exemplo o caso da igualdade y = f(x), encontramos a variável y dependente da variável x, isto já é uma função, não equação.
Ainda neste capítulos abordaremos aspectos de relevância importância para a resolução de equações irracionais como é o caso da monotonia da função real de variável real, destacando a variação do sinal da função linear do 1º grau e a função quadrática que são encontradas com maior frequência no decurso da resolução de equações irracionais, dando deste modo vários exemplos para habilitar os estudantes e relembrar estes aspectos aos Docentes.
1.1– Conceito de equação
Dadas duas funções reais y = f(x) e y = g(x), com domínio de definição D1 e D2 respectivamente.
A igualdade formal:
f(x) = g(x) (1)
Denomina – se equação com incógnita x.
Se se observar devidamente nota – se que a expressão (1) compara duas funções duma forma igual ou melhor utilizando o sinal de igualdade, visto que elas dependem duma variável x, mas não necessariamente ambas terem dependência da variável x.
Exemplo1
a) Quando f(x) = ax + b e g(x)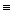 
0,
A equação (1) toma forma
ax + b = 0, que é uma equação linear do 1º grau com incógnita x(variável independente).
b) Quando f(x) = ax² + bx + c e g(x) 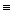0,
tem – se:
ax² + bx + c = 0 que é chamada equação quadrática.
c) Quando f(x) = sen2x, g(x) = cosx, obtem – se:
sen2x = cosx que é uma equação trigonométrica.
1.2 – Equação algébrica.
Dada a equação
f(x) = g(x) (1)
Onde f(x) e g(x) são expressões algébricas. Então a equação (1) é chamada equação algébrica.
Uma equação algébrica pode ser inteira ou fraccionária.
Inteira se f(x) e g(x) forem expressões algébricas inteiras,
Por exemplo:
2x³ + x² + 4x + 1 = 0 ? equação algébrica inteira.
Fraccionária se a equação (1) f(x) e g(x) forem expressões algébrica fraccionária,
Por exemplo:
+ 
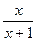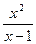= 0 ? Equação algébrica fraccionaria
1.3- Equação irracional
É uma equação algébrica, na qual pelo menos um membro da equação contém raiz de expressão da incógnita.
Exemplo1
Seja
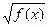= h(x),
consideremos f(x) = x² – 4
h(x) = 1 – x
Temos:
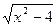= 1– x ? uma equação irracional, pois que no membro esquerdo da equação tem um radical em que no seu radicando existe uma incógnita x.
Vejamos a seguinte equação
x + 123 = 2x -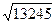 
No seu membro direito temos um radical cujo seu radicando é um número e não uma incógnita. No entanto podemos afirmar com clareza que não é uma equação irracional, porque não tem nenhuma incógnita no radicando.
1.4– Conceito de solução
Seja
f(x) = g(x) (1)
Um valor x0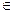
D1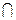
D2 tal que f(x0) = g(x0), é chamada solução da equação (1).
Resolver a equação (1) é achar o conjunto de todos os valores x0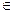D1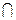D2 tais que f(x0) = g(x0).
O conjunto das soluções da equação (1) denota – se por S.
O conjunto S pode ser finito, vazio ou mesmo infinito, conforme se apresentam os exemplos que se seguem:
x² - 2x + 1 = 0 S = {1 } conjunto finito
x² + x + 1 = 0 S = {Ø} conjunto vazio
Senx = 0 S = {k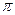 
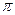
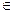: Z } conjunto infinito
1.5 – Equação equivalente
Diz – se duas equações são equivalente se têm o mesmo conjunto solução.
f(x) = g(x) é equivalente a equação h(x) = k(x) se tiverem o mesmo conjunto solução e podemos representar pelo sinal de equivalência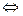 
, por:
f(x) = g(x) 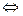h(x) = k(x).
Exemplos
Exemplo 1
Sejam dadas as seguintes equações:
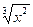= 1 (1)
x² - 1 = 0 (2)
O conjunto solução da equação (1) e da equação (2) é o mesmo S = {-1; 1}, logo são equivalentes.
Exemplo 2
Dadas as equações
= 
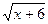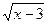(3)
x² - 9 = 0 (4),
Resolvendo (3) e (4) notar – se - a que a equação 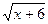= 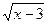(3) o conjunto solução é S3 = { 
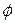} e a equação x² - 9 = 0 (4) o conjunto solução é S
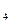= {– 3; 3}. Não são equivalentes porque não tem o mesmo conjunto solução, pois que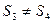 
Exemplo 3
Observa novamente as seguintes equações
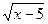= 0 (5) e
x³ + 8 = 0 (6)
Também não têm o mesmo conjunto solução, visto que para a equação (5) temos o conjunto solução S5= {5} e para a equação (6) temos S6= {2}. Por isso não são equivalente,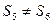 
1.6 – Equação consequente
Sejam duas equações: f1(x) = g1(x) (1)
F2(x) = g2(x) (2)
e sejam S1 e S2, conjuntos solução das equações (1) e (2) respectivamente. Se S1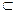 
S2, diz – se que a equação (2) é equação consequente da equação (1).
Denotando – se
F1(x) = g1(x)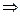 
f2(x) = g2(x) (2)
Exemplo ilustrativo:
Dada a equação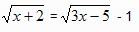 
(1)
Resolvendo:
Elevando ambos os membros da equação ao quadrado tem – se
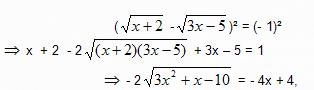
Passando o 2 ao membro direito a dividir,
tem – se
- 
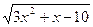= - 2x + 2
Elevando mais uma vez ambos os membros ao quadrado teremos
3x² + x – 10 = 4x² - 8x + 4
agrupando os termos semelhantes e fazendo a devida operação obtém – se a equação
x² - 9x + 14 = 0 (2).
factoriazando (2) teremos
(x - 2)(x - 7) = 0
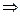x - 2) = 0
(x - 7) = 0
Logo
X1 = 2
X2= 7.
O conjunto solução da equação (2) é S = {2; 7}.
Mas se substituirmos os valores deste conjunto na equação (1) veremos que um dos dois elementos do conjunto não satisfaz a equação.
Começando por substituir o 2 temos:
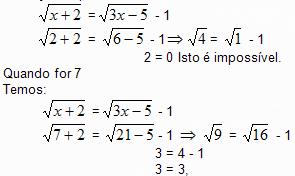
Contudo 7 satisfaz a equação (1) mas 2 não.
Para a equação (2) substituindo o 2
Temos:
x² - 9x + 14 = 0
(2)² - 9(2) + 14 = 0
4 – 18 + 14 = 0
0 = 0
Substituindo o 7 temos:
x² - 9x + 14 = 0
(7)² - 9(7) + 14 = 0
49 – 63 + 14 = 0
0 = 0
Observa que 2 e 7 satisfazem a equação (2)
Então para a equação (1) o conjunto solução é S1 = {7} e para a equação (2) é S2 = {2; 7}
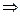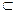S1 S2
Portanto a equação (2) é equação consequente da equação (1).
2 - Transformação
No decurso de resolução de uma equação empregamos sempre três sentidos de transformação que consiste em transformar a equação de modo que facilite a sua resolução e leve a uma solução que satisfaça a equação original, são elas: Transformação equivalente ou que não muda o domínio de definição da equação, transformação que estende o domínio de definição e a que estreita o domínio.
2.1 – Transformação que não muda o domínio de definição da equação (transformação equivalente).
Nesta transformação a equação transformada não altera o seu domínio em relação a equação original, o que quer dizer que a equação original e a equação transformada terão o mesmo domínio de definição, o que fará com que ambas equações sejam equivalente.
Por exemplo:
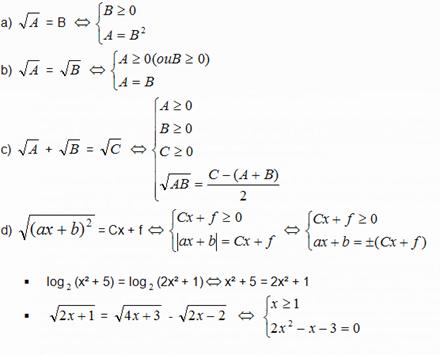
2.2 – Transformação que estende o domínio de definição da equação.
Com esta transformação a equação obtida é uma equação consequente da original, o que quer dizer que verifica - se a ampliação do domínio que define a equação original, conforme constatou – se quando abordou – se sobre equação consequente, aparece no conjunto solução uma raiz estranha derivada da equação transformada.
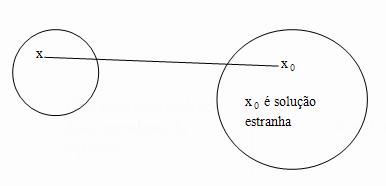
Exemplo1
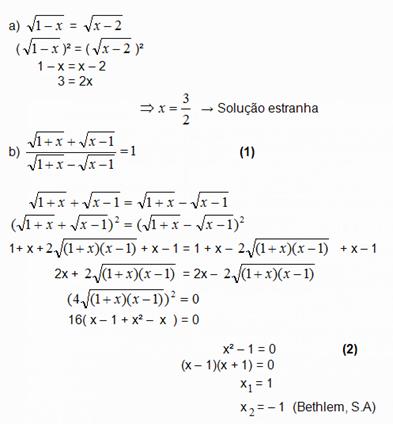
No conjunto solução de (2)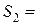 
{ - 1; 1 } existe uma raiz estranha a equação (1), esta raiz é – 1.
Se se Substitui – 1 na equação (1) veremos que não satisfaz, por isso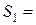 
{ 1 }
Portanto a transformação feita de (1) para (2) ampliou o domínio de definição da equação (1).
2.3 – Transformação que estreita o domínio de definição da equação.
Já para esta transformação, necessariamente o domínio de definição da equação será restringido, transformando - a numa equação de resolução mais simples e conveniente.
Exemplo1
Consideremos a seguinte equação trigonométrica:
2senx – cosx = 1 (1)
Transformemos esta equação numa equação
- 
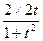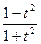= 1 (2)
Considerando para senx =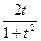 
e
cosx = 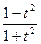onde t = tg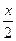 
esta transformação naturalmente que estreitará o domínio de definição da equação.
Achando o valor de t temos:
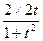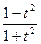- = 1
4t - (1 - t²) = 1 + t²,
eliminando os parênteses e simplificando os t² temos
4t = 2
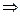t =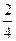 
t =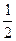 
Usando para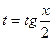 
, onde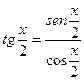 
Com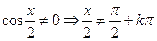 
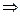
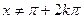
Então se 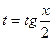e na transformação feita encontramos t =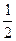
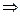
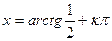
Portanto podemos considerar como domínio de definição da equação (1)
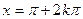
Se se substituir 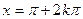na expressão (1) obtém – se
2sen(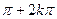 
) – cos( 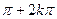) = 1 para k = 0,1,2,3..
Quando k = 0
tem – se
2sen( 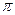) – cos( 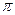) = 1
0 – (- 1) = 1
1 = 1
Exemplo2
Seja a equação
x² = 4 (3)
para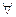 
x tal que o domínio de definição da equação é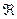 
Se usarmos a operação colocando ambos os membros da equação (3) nos radicais como radicandos temos:
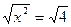(4)
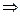x = 2.
Repara que a equação (3) x² = 4 necessariamente x =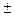 
2. A transformação feita de (3) para (4) estreita o domínio de definição da equação (2), porque enquanto para a equação (3) x = 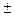2 para a equação (4) x = 2.
3 - Monotonia da função real de variavel real
Se observamos com clareza e bastante atenção a um dado gráfico notaremos que a medida em que se vai da esquerda para a direita pelas abcissas, independentemente do sentido em que o gráfico for a tomar, vai se tendo ordenadas cada vez maior se a função estiver a crescer e cada vez menor se a função for decrescendo.
Definição:
A variação da função de modo a crescer ou a decrescer, Chama – se Monotonia.
Seja f uma função qualquer e seja A um subconjunto do Dominio de definição da função (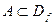 
) e a e b pertencentes a A.
Diz – se que:
f é uma função crescente em A
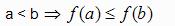
f é uma função decrescente em A
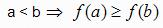
4 - Variação da função linear do primeiro grau e da função quadrática.
4.1 – Variação da funçao linear do primeiro grau.
Teorema 1: A função f(x) = ax + b quando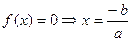 
, então
a) a > 0, a função é crescente
b) a < 0, a função é decrescente
Demonstração:
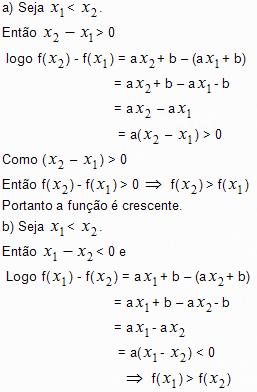
Portanto a função é decrescente.
Teorema 2:
Dada a função
f(x) = ax² + bx + c
Suponhamos qu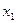e 
e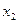 
são duas raízes reais diferentes quando f(x) = 0, com <
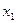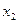
Então:
a > 0
a função toma o sinal positivo fora do intervalo que é o mesmo sinal do coeficiente a e o sinal contrário do coeficiente a dentro do intervalo.
a < 0
a função toma o sinal negativo fora do intervalo que é o mesmo sinal do coeficiente a e o sinal contrário do coeficiente a dentro do intervalo.
Demonstração:
Se a equação f(x) = ax² + bx + c = 0
Tem duas raízes distintas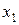 
< 
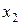Então a função f(x) pode escrever – se sob a forma:
f(x) = a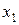(x - )(x - ).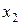
No entanto se estabelece a tabela de variação
Caso1: a > 0
Obs1: Fora do intervalo das raízes a função toma o sinal positivo que é o mesmo sinal do coeficiente a e o sinal contrário do coeficiente a dentro do intervalo.
Caso 2
Obs2: Fora do intervalo das raízes a função toma o sinal negativo que é o mesmo sinal do coeficiente a e o sinal contrário do coeficiente a dentro do intervalo.
Assim conclui – se que em ambos os casos o sinal do coeficiente a é o mesmo que da função fora do intervalo das raízes e contrário dentro do intervalo.
Exemplo1
Dada a função linear do 1º grau f(x) = – 12000x + 1
a) Encontrar o valor de x para f(x) = 0.
b) Estudar o sinal da função
c) Estudar o sinal da função para f(x) = – 12000x
Solução:
a) Para f(x) = 0 tem - se
– 12000x + 1 = 0
x =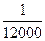 
b) Para se estudar esta função empregamos o teorema 1
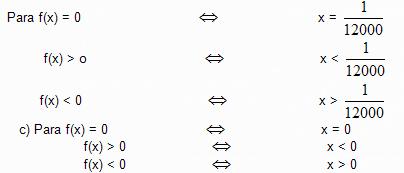
Exemplo2
Considerar o gráfico
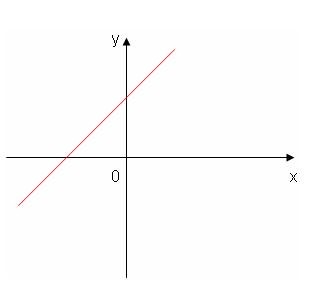
a) Que representa o gráfico desta função?
b) Quais dos quadrantes ocupa o gráfico?
Solução:
a) A função que representa graficamente este sentido em recta é a linear
f(x) = ax + b
b) A função ocupa o 1º e o 3º quadrante conforme o sentido do gráfico
Exemplo3
Dada a função quadrática
f(x) = 100x² + x
a) Quais são os zeros da função dada?
b) Que sinal toma a função nos pontos
X1= 999
X2= – 786
Solução:
a) Para achar os zeros da função igualamos f(x) = 0
Então
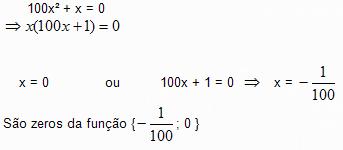
b) Primeira maneira (Calculo Direito)
f(x1) = 100 (999)² + 999
f(999) = 100 (999)² + 999
= 100(998001) + 999
= 99800100 + 999
= 9980199
f(x2) = 100(x2)² + (x2)
f(- 786) = 100(- 786)² + (– 786)
= 100(617796) – 786
= 61779600 – 786
= 61778814
Portanto a função nos pontos x1= 999 e x2= – 786 toma sinal positivo.
Segunda maneira (Uso do teorema2)
Como x1 = 999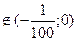 
Segundo o teorema2, f(x1) = f(999) é positivo.
Como x2= – 786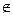 
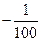;0)
Segundo o teorema2, f(x2) toma o sinal do coeficiente a (a = 100) por isso f(– 786) > 0
Capitulo II
Há vários métodos para a resolução das equações irracionais. Um dos métodos frequentemente aplicado é de uso das transformações equivalentes.
Neste Capitulo concentra – se a apresentação deste método. Alem disso apresentamos outros métodos especiais, tais como:
Método de uso da desconhecida auxiliar
Método da função monótona
1 – Método de transformação equivalente
Este método tem as vantagens seguintes:
E aplicável para maior parte das equações irracionais
Não adiante solução estranha, por isso pode – se eliminar o passo verificação das soluções encontradas.
Na presente secção empregamos as transformações equivalentes mencionadas no Capitulo I, classificando os tipos ao nível da sua dificuldade
1.1 – Equação da forma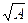 
= B
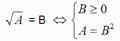
onde A, B são binómios e em caso mais geral A ou B são trinómios
Caso 1: A, B são binómios
Exemplos
Exemplo1: Resolver as equações
a)
b)
Solução:
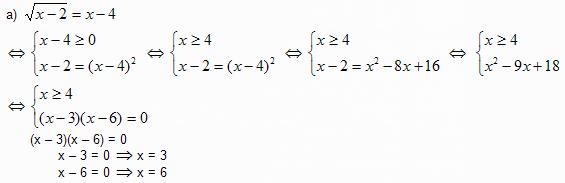
Pela condição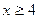 
a raiz x = 3 é excluída.
Portanto
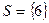
b)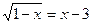 
A condição para esta equação é dada por
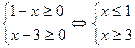
Pela condição x = 1 e x = 3 Só e só se a equação é impossível.
Exemplo2
Resolver a equação
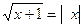
Solução:
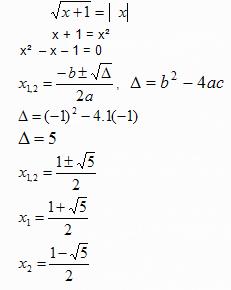
Exemplo3
Dada a equação
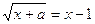
a) Determinar os valores de a tal que a equação seja possível
b) Resolver a equação para a = – 1
Solução:
Nota: Na resolução da equação da forma do tipo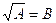 
foi empregada a transformação equivalente. Contudo em alguns problemas concretos podemos usar a transformação que estende o domínio de definição da equação, apresentando possivelmente a solução estranha. Neste caso é obrigatório verificar se a solução obtida satisfaz ou não a equação dada.
Exemplo1
Resolver a equação
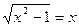
Solução:
Elevando os dois membros da equação, obtemos uma equação consequente
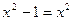
– 1 = 0 é impossível.
Exemplo2
Dada a equação
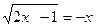
Resolver tendo em conta a transformação consequente
Solução:
Elevando ambos os membros ao quadrado, obtém – se
2x – 1 = (– x )²
2x – 1= x²
x² – 2x + 1= 0
(x – 1)² = 0
x = 1
Verificação
Pela substituição do valor de x que é igual a 1, na equação obtém – se
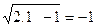
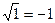isto é impossível
Conclusão: a equação é impossível.
Exemplo3
Retoma – se o exemplo da pag.25 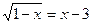a alínea b)
Solução:
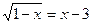
Elevando os dois membros da equação ao quadrado tem – se
1 – x = (x – 3)²
1 – x = x² – 6x + 9
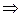x² – 5x + 8 = 0
Utilizando a formula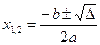 
onde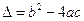 
Substituindo os valores de a, b e c temos:
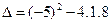
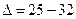
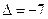
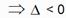, Logo a equação é impossível.
Caso2: A ou B é trinómios
Exemplo1
Dada a equação
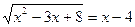
a) Achar o valor de x que satisfaz a equação dada
Solução:
Sob a condição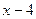 
0 ou seja x = 4
Temos:
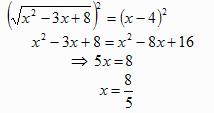
Conclusão: A equação é impossível.
Exemplo2
Resolver a equação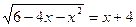 
(1)
Solução:
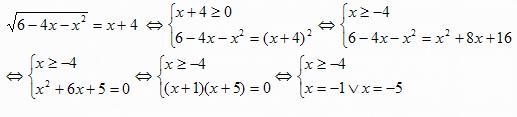
A solução x = – 5 é excluída por causa da condição de que x = – 4.
Conclusão
x = – 1
Exemplo3
Resolver a equação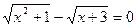 
Solução:
Caso1: A, B são Binómios
Exemplo1
Resolver as seguintes equações
a)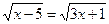 
b)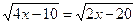 
Solução:
a)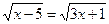
Conclusão:
x = 15
Caso2: A, B são trinómios
Exemplo1
Encontrar valores para x da equação
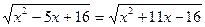
Solução:
Como x² – 5x + 16 = 0, 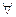x tem – se
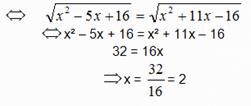
Exemplo2
Resolver a equação
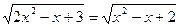
Solução:
Como x² - x + 2 = 0 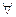x
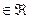tem – se
Exemplo1
Dadas as equações
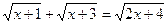(1)
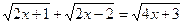(2)
a) Resolver
Solução:
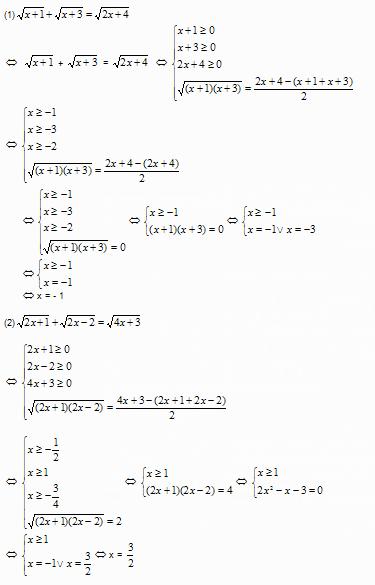
Nota: Caso em que A, B, C são trinómios, as vezes emprega – se a equação consequente com verificação obrigatória das soluções obtidas.
Exemplo2
Dada a equação
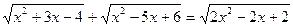
a) Transformar a equação dada em uma equação consequente.
b) Resolver a equação dada
Solução:
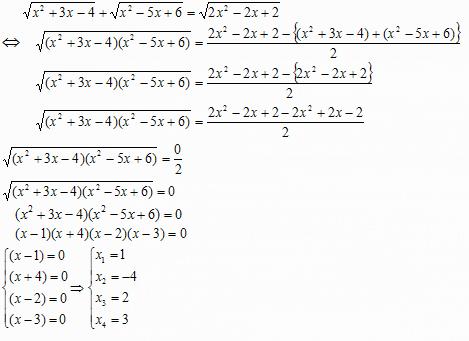
Verificação
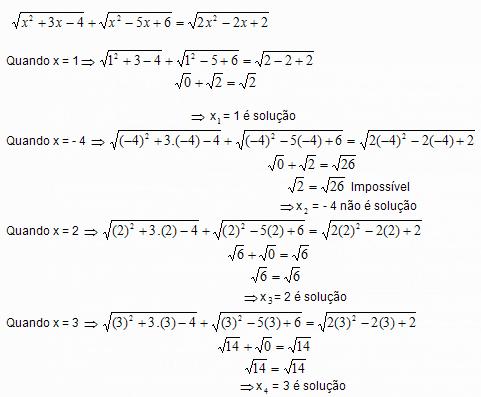
Portanto S = { 1; 2; 3}
2– Método do uso da desconhecida auxiliar
Este método é aplicável a equação mais complicada. A desconhecida auxiliar é escolhida de maneira razoável de acordo a equação concreta, permitindo a reduzir em outra mais simples.
Nesta secção estudam – se apenas alguns casos especiais.
Caso1 Equação da forma
af(x) + b 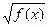+ c = 0
Neste caso emprega – se a desconhecida auxiliar t = 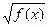com condição t = 0.
Exemplo1
Resolver a equação
Caso2: Equação da forma
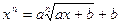
Com ajuda da desconhecida auxiliar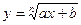 
obtemos um sistema de equações simétricas:
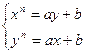
Exemplo: Resolver a equação
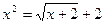
Solução:
Se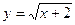 
temos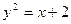 
Obtemos o sistema
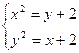
Subtraindo a segunda equação do sistema da primeira, obtém – se
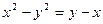
(x – y)(x + y) = y – x
(x – y)(x + y) + x – y = 0
(x – y)(x + y + 1) = 0
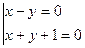
Quando y = x temos
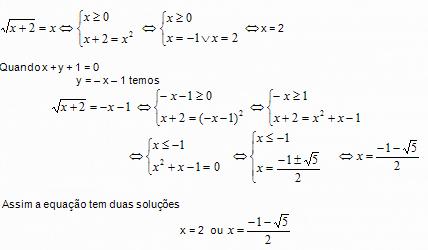
Caso3: Equações de diversas formas
Resolver as equações seguintes
Conclusão: A equação (3) tem duas soluções x = 0 v x = 1
3– Método da monotonia
3.1 – Consideremos a equação da forma
f(x) = g(x) (1)
Em alguns casos especiais:
Caso 1: Se f(x) é uma função estritamente monótona (isto é estritamente crescente ou estritamente decrescente ) e g(x) é igual a constante C, então a equação
f(x) = C
Tem possivelmente uma solução única x = x0
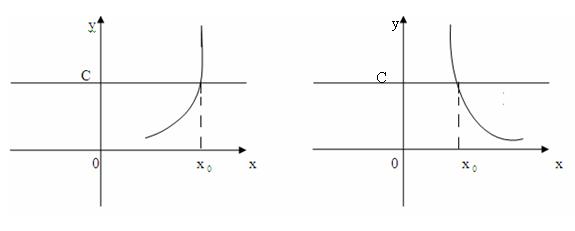
Caso 2: Se f(x) é uma função crescente e g(x) é decrescente então a equação tem possivelmente uma solução única x = x0
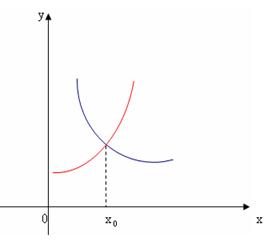
3.2 – Aplicações
Exemplo1
Dada a equação
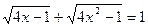
a) Determinar a condição para que a equação tenha sentido
b) Empregando a monotonia da função ao membro esquerdo resolve – lá.
Solução:
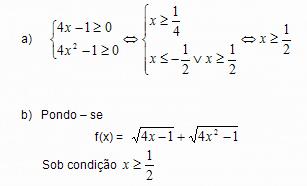
Temos
Exemplo3
Resolver a equação
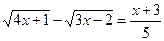
Solução:
Multiplicamos os dois membros da equação pelo conjugado do membro esquerdo
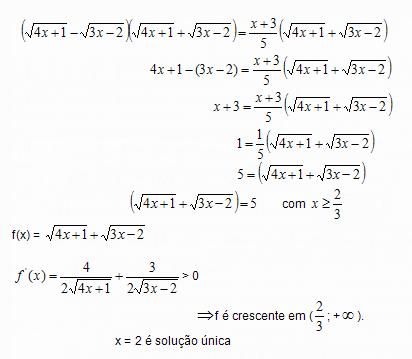
Resumo das investigações iniciais
Os dados recolhidos permitiram conhecer de uma forma geral o nível de conhecimentos, bem como os erros que frequentemente cometem os alunos da 12ª classe do PUNIV Joaquim Capango na área de Ciências Físicas – Biológicas ao resolverem exercícios relativamente a equações equivalentes e irracionais.
Nesta senda foram inquiridos 187 alunos, que corresponde a 38,95% a amostra da população estudada.
O tipo de pesquisa é quantitativo, e qualitativo que permitiu a realização de procedimentos estatísticos variados e adequados a cada situação específica tendo como objectivo exploratório, visto que permitiu entender as dificuldades em causas.
Escolhi os alunos da 12ª classe do PUNIV pelo facto de ser uma Instituição que mais candidatos dá nos concursos de ingresso ao ensino Superior e tem sido uma Instituição muito mais problemática em relação as de formações profissionais.
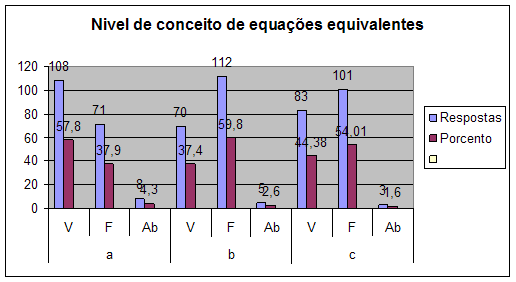
O gráfico 1- Mostra -nos o nível de conhecimento dos alunos sobre o conceito de equações equivalentes.
Conclusão:
Analisando atentamente o gráfico, verificamos que para a alínea b) que é a verdadeira tem maior percentagem ao número de alunos que afirmam ser falsa portanto há pouco domínio no que concerne o conceito de equações equivalentes, devendo se trabalhar para superar pelo facto do conceito ser fundamental para os demais aspectos.
Quadro – 2
Apresenta a capacidade de análise que os alunos têm ao identificar ou diferenciar uma equação equivalente de uma não equivalente.
|
Questão 2 |
Certas |
Erradas |
Abstinências |
Amostra |
|
|
a) b) c) |
72 |
100 |
15 |
187 |
|
|
% |
38,50 |
53,47 |
8,02 |
100 |
|
Conclusão:
A capacidade de análise que os alunos têm ao identificar e diferenciar equações equivalentes e as não equivalentes é relativamente baixa, conforme mostra a tabela onde maior percentagem de alunos assinalaram a alinea b) que não são equivalentes, confirmando deste modo a dificuldade no conceito e dificultando de maneira a sua diferença ou identificação, pelo que urge a necessidade de disponibilizar mais bibliografias aos alunos para sua profunda investigação.
.
Gráfico 3: Representa os resultados da questão 3 que consiste em avaliar o grau de conhecimento sobre o conceito de equações irracionais.
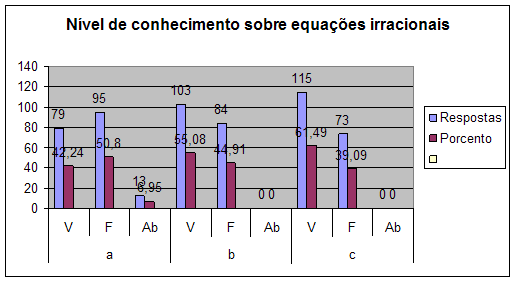
Conclusão
A alínea verdadeira é a alínea a). No entanto explica-se que existe fraco conhecimento por parte dos estudantes da condição de conceito de equações irracional, ao afirmarem com maior número nas falsas b) e c) embora com pouca diferença percentual com a verdadeira.
Gráfico 4: Mostra a capacidade e o nível de conhecimento e análise que os alunos têm em diferenciar uma equação irracional de uma não irracional.
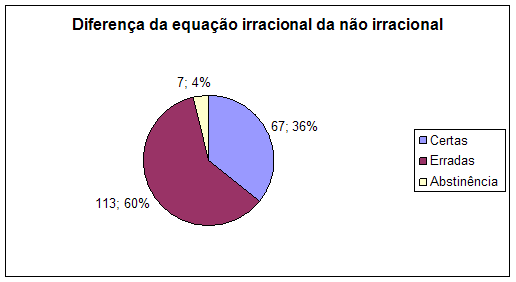
Conclusão
Dos 187 estudantes inqueridos, quanto a esta questão, 67 estudantes acertaram marcando a alínea a) fazendo uma percentagem de 36 % inferior a 60% de estudantes que erraram indicando as alíneas b) e c) num número de 113 e 7 abstiveram 4%.
Portanto o nível de conhecimento, habilidade que os alunos têm em diferenciar uma equação irracional de uma não irracional é baixo. O que prova pouco conhecimento sobre o conceito de equação irracional, justificando assim a necessidade de aumentar métodos eficazes para facilitar o desenvolvimento técnico dos alunos na diferenciação e resolução de equações irracionais.
Gráfico 5: Descreve as habilidades dos alunos em rever se a solução da equação é valida ou não.
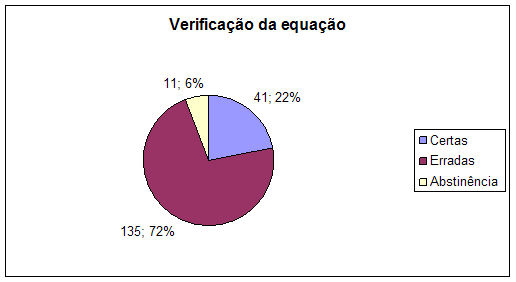
Conclusão
Pouca habilidade e capacidade dos alunos em verificar se a solução é válida ou não, pelo que mais bibliografias devem ser dispostas ao alcance dos alunos para que haja aprendizagem sólida, desenvolvendo as habilidades e capacidades.
.
Quadro – 6
Analisa o interesse dos alunos em resolver exercícios de equações irracionais e interpretação do que eles acham quanto ao grau de dificuldades.
Conclusão:
Os estudantes têm grande interesse e gosto em resolver exercícios de equações irracionais no que mostra a tabela, numa percentagem de 72,19% a favor de 26,2%, abstendo-se 1,6%, pelo que, deve - se incrementar métodos viáveis para que se suprima as dificuldade registadas.
A alínea a) é para avaliar o grau de preocupação psicológica quanto ao interesse de resolução. E a tabela nos esclarece que maior parte dos alunos acham não ser difícil resolver uma equação irracional, mas uma pouca diferença percentual, algumas afirmam ser difícil o que nos leva a crer que pode se minimizar as dificuldades que os alunos têm, trabalhando para que os estudantes na sua maioria incomparável saibam que não é difícil resolver, basta aplicação.
Quadro 7
Descreve as dificuldades em resolver uma equação
Conclusão
Para consumar com bastante clareza a 7ª questão procura saber se os alunos têm ou não dificuldades em resolver uma equação irracional e numa percentagem superior eles afirmam terem dificuldades, sim, razão pela qual 68,44% contra 29,94% com 1,6% abstenções.
Gráfico 7 - a)
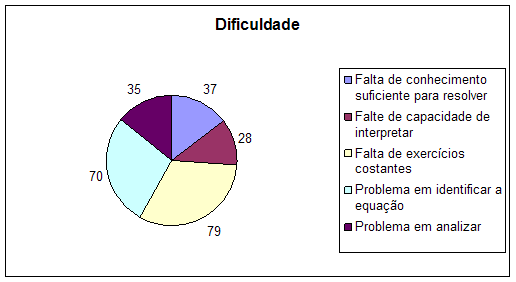
Já neste gráfico os alunos indicam os elementos fundamentais que consiste na grande dificuldade de entendimento de resolução das equações irracionais, assinalando um maior número de alunos na falta de exercícios constantes, problema em identificar a equação o que quer dizer que entendem pouco o conceito e não praticam nem resolvem exercícios independentes (tarefa).
Resultado dos inquéritos aplicados aos professores.
Questão 1
No gráfico seguinte tem – se as respostas dos Docentes quanto ao material de apoio.
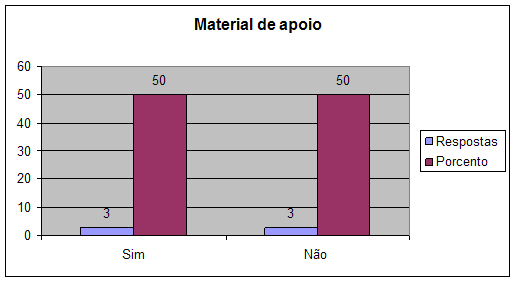
Conclusão:
Conforme nos ilustra o gráfico, percebemos que no total de professores, existe um equilíbrio quanto ao material de apoio que têm, o que quer dizer 50% de professores têm o material de apoio e os restantes 50% não têm.
Questão 2
Resposta, temos o gráfico 2 que representa o aproveitamento dos alunos.
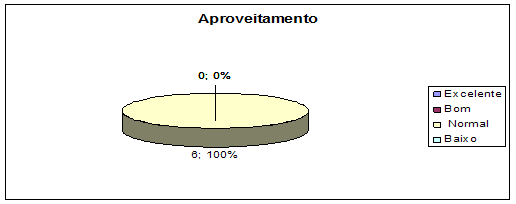Graf.2
Conclusão
Os professores indicam com a maioria absoluta o aproveitamento dos alunos sendo normal, o que se tem para trabalhar e chegar a um aproveitamento excelente.
Questão 3
A seguir temos o gráfico que indica a resposta quanto ao número de métodos usados pelos docentes.
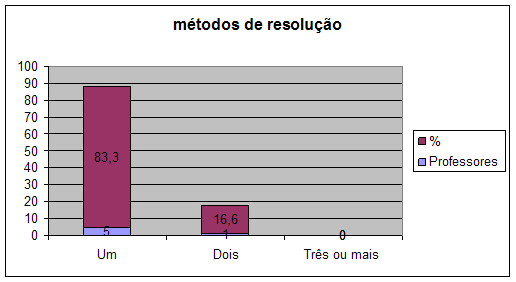
Conclusão
Dos seis (6) professores inquiridos cinco (5) utilizam apenas um método de resolução e somente um professor utiliza dois métodos, contudo este trabalho trás mais de um método de resolução contribuindo assim para o engrandecimento do ensino e aprendizagem.
Questão 4
Na tabela seguinte se mostra a resposta.
|
Resposta |
Professores |
% |
|
Sim |
6 |
100 |
|
Não |
00 |
00 |
Conclusão:
Analisando atentamente a tabela verificamos que todos os professores acham ter um método de resolução mais simples, indicando o método de elevar ambos os membros da equação ao quadrado, o que não corresponde com o certo, visto que, em função ao grau de dificuldade emprega – se o método adequado de modo a facilitar a sua resolução.
Questão 5
Resposta, tabela seguinte.
|
Respostas |
Professores |
||
|
Pouco tempo de aula |
6 |
||
|
Fraco aproveitamento nos conteúdos antecedentes |
6 |
||
|
Poucos métodos a utilizarem |
2 |
||
Conclusão
Na administração das aulas os professores dizem encontrar dificuldade no que concerne ao pouco tempo de aula e o fraco aproveitamento dos conteúdos de base para o tema em assunto.
Questão 6 – Conclusão
Duma forma geral os professores acham que o tema é de grande importância porque para alem de minimizar as dificuldades encontradas pelos alunos, habilitar e capacitar os alunos na resolução de equações irracionais, apoiar o material Docente, ainda ajudará os professores na preparação das suas aulas sobre equações irracionais contribuindo ao processo de ensino – aprendizagem.
Conclusões
De acordo objectivos previstos e em função do problema, analisados os dados recolhidos chega – se as seguintes conclusões.
Os alunos aprendem equações equivalentes e resolvem as equações irracionais parcialmente.
Abordar a resolução de equações irracionais, implica a análise de diferentes casos o que se explicita a partir de diferentes exemplos seleccionados com este objectivo.
Pelo facto do débil domínio dos alunos no conceito de equações equivalentes e irracionais conclui – se a grande dificuldade que apresentam desde os pormenores básicos.
Pouca criatividade no incentivo dos alunos nas resoluções de equações irracionais.
É pertinente dispor mais exercícios em que se aplicam métodos de resolução em função ao grau de dificuldade.
É necessário encontrar vias adequados para capacitar os alunos na diferenciação dos vários tipos de equações.
É fundamental nas aulas administradas que se relacionem conteúdos básicos, aprendidos em classes anteriores, referindo – se concretamente sobre equivalência.
A tendendo a grande importância deste trabalho de investigação com finalidade de pesquisa, para melhorar o processo de ensino e aprendizagem, recomenda – se o seguinte:
É importante que as Instituições de ensino Médio, particularmente os professores que leccionam a 12ª classe do PUNIV façam uma análise dos aspectos metodológicos que se abordaram na investigação da resolução das dificuldades na aprendizagem dos alunos.
Tendo em conta que os alunos de ciências físicas – biológicas venham ser os futuros engenheiros particularmente na área petrolífera, devem investigar e dominar equações irracionais por ser um conteúdo muito utilizados nesta engenharia.
O material em causa se ponha ao alcance de todos que o precisarem.
ÁLVAREZ, C. Matemática para uma escola de excelência. 3ª Edição; Editorial Academia, Cidade de Havana (1996).
ANDERSON, L. GQuilles, Cláudio, H. Bitto; Matematica essencial – Internet; 2005.
ARANHA, Álvaro Zimmerann; Funções e Logaritmos; 2ª Edição; Policarpo Ltda Editora; 1994.
BETHLEM, Agrícola; Matemática moderna; 2ª edição; S.A.
BALLESTER, S. e outros (1992). Metodologia do Ensino da Matemática, Tomo I, Editorial Povo e Educação, Havana 2ª Edição.
COSTA, António de Almeida, Alfredo Osório dos Anjos: Compendio de Matemática; 4ª Edição; Porto Editora, Lda, 1973.
CRUZ, Amabilia, M. Emília Vázques et al; Matemática 9º ano de escolaridade; Porto Editores; 2ª Edição; S.A.
DAVINSON, Luis J. (1964). Guia para o Professor; Ensino Médio Básico; Ministério de Educação, 2ª Edição; Cidade Liberdade, Cuba.
Exercícios resolvidos Matemática, 12º ano I volume, S.A
FAZENDA, José António; Matemática 12ª classe; 1ª Edição; Texto Editaras, LDA; 2007
GIRAO, Pedro; Sérgio Valente, Matemática 12º ano Volume II; 2ª Edição; Platónico Editora, S. A.
GONZÁLEZ, M.O. (1967a). Algebra Elementar Moderna. Vol. 1. Editora Pedagógica.
GONZÁLEZ, M.O. (1967b). Matemática. Quinto curso. Complementos de Geometria e noções de Cálculo Diferencial e Integral. Ed. Povo e Educação
GONZÁLEZ, P. e H, Valdés (1992). Psicologia Humanista atualidade e desenvolvimento, Editorial Ciências Sociais. Havana.
HERNÁNDEZ, H. e outros (1997). Um recurso metacognitivo para resolução de problemas em Matemática: O auto controlo. Exposição em Pedagogia´97. Cidade de Havana
IEZZI, Gelson; Fundamentos de Matemática elementar; 8ª Edição; São Paulo Editoras; 2004.
JUNGK, W. (1979). Conferencia sobre Metodologia do Ensino da Matemática. Primeira parte. Ed. Livros para a Educação, Cidade Havana.
JUNGK, W. (1979b). Conferencia sobre Metodologia do Ensino da Matemática. Segunda parte. Ed. Livros para a Educação, Cidade Havana.
JORGE, Ana Maria Brito, Conceição Barroso Alves, at al; Matemática 12º ano; 3ª Edição; Areal Editores; S.A.
MACHADO, António dos Santos, Conjuntos e Funções; 2ª Edição; São Paulo; 1998.
NEVES, Maria Augusta Ferreira; Maria Luísa Carvalho Brito; 9º ano de escolaridade; 4ª Edição; S.A.
NEVES, Maria Augusta Ferreira; Matemática 10ª classe; 2ª Edição; Porto Editora; 2005.
NEVES, Maria Augusta Ferreira; Matemática 12ª classe; 1ª Edião; Porto Editora; 2006.
RIBNIKOV, K. (1987). História da matemática; 2ª Edição Editorial Mir, Moscou.
SAFIER, Fred; Teoria e Problema de pré – calculo; 1ª Edição; Porto Alegre Editoras; 2003.
SIGARRETA, J. (2001). Incidência do tratamento dos problemas matemáticos na formação de valores. Tese de Doutorado. ISP"José da Luz e Cavalheiro", Holguín.
www educ.f c. ul.pt/ docentes/ j ponte/ temporário/ MEM/ T2.
www. Ufpi/ br/ downloads/ uploads/.
www. Somatematica.com educ.f c. ul.pt/
Autor:
Bartolomeu Chindumbo Delfino
chindumbo27h[arroba]yahoo.com.br
| Página anterior | Voltar ao início do trabalho | Página seguinte |
|
|
|
