Fisica. Estática y cinemática

1
23
28
39
40
44
46
52
55
58
INDICE

P᧩na
FISICA CERO Matemᴩca necesaria para entender f�ca
20
ESTATICA
22………… FUERZAS COPUNTUALES
SUMA DE FUERZAS 栒ESULTANTE
25………….TRIGONOMETRIA. SENO, COSENO Y TANGENTE
PROYECCIONES DE UNA FUERZA
31…………. SUMA DE FUERZAS ANALITICAMENTE
33
EQUILIBRIO
35…………..EJEMPLOS

39…………. FUERZAS NO COPUNTUALES
MOMENTO DE UNA FUERZA
39………….. SIGNO DEL MOMENTO
EQUILIBRIO PARA FUERZAS NO CONCURRENTES
42………….. EJEMPLOS
TEOREMA DE VARIGNON
45………….. CENTRO DE GRAVEDAD
PROBLEMAS TOMADOS EN PARCIALES

CINEMATICA

MRU
Posici㮬 velocidad y aceleraci㮮
53 ……….. Sistema de referencia. Trayectoria.
Movimiento Rectil�o y Uniforme
57……….. Velocidad en el MRU
Ecuaciones horarias en el MRU
59 ……….. Tg de un ᮧulo y pendiente de una recta.
61
Grᦩcos en el MRU
62…………. Pendientes y las Ქas de los grᦩcos
63
Un ejemplo de MRU
67…………. Velocidad media

75
86
88
93
96
100
116
133
137
153
160
73 ……….. ENCUENTRO.
Problemas de encuentro.
81 ……….. Encuentro cuando un m㶩l que sale antes que el otro
83
MRUV
84 ……….. Aceleraci㮮
Signo de la aceleraci㮍
87………… Ecuaci㮠de una par᢯la
Soluci㮠de una ecuaci㮠cuadrᴩca
89 ……….. Ecuaciones y grᦩcos en el MRUV
Ecuaci㮠complementaria.
95 ……….. Velocidad instantᮥa.
Anᬩsis de los grᦩcos del MRUV
98…………. La velocidad y la aceleraci㮠son vectores
Como resolver problemas de MRUV
101…………..MRUV, Ejercicios de parciales
105
Encuentro en MRUV
107…………. Encuentro, Ejercicios de parciales

113 …………CÄ́A LIBRE Y TIRO VERTICAL
Como resolver problemas de C. libre y Tiro vertical
123…………Ca� libre, ejercicios de parciales

127 ……….. TIRO OBLICUO
129
Trigonometr�
131………….Proyecci㮠de un vector
Principio de independencia de los movimientos de Galileo
136………….Ecuaciones en el Tiro Oblicuo.
Como resolver problemas de Tiro Oblicuo
138………….Ejemplos y problemas sacados de parciales

MOVIMIENTO CIRCULAR
154…………. Movimiento circular uniforme
154
El Radiᮍ
156…………..La velocidad angular omega
157
La velocidad tangencial
157…………..Per�o T y frecuencia f
158
Aceleraci㮠centr�ta
159…………..Relaci㮠entre ? y f
Algunos problemas de Movimiento circular

164
167
173
179
184
MOVIMIENTO RELATIVO
165…………..Velocidades relativa, absoluta y velocidad de arrastre
Algunos problemas de Movimiento relativo

CINEMATICA VECTORIAL
174…………..Vectores
175
Componentes de un vector
177…………. M㤵lo de un vector
Vector Posici㮠y vector desplazamiento
180…………..Vector Velocidad Media
182
Velocidad instantᮥa
184…………. Aceleraci㮠Media e instantᮥa
Ejemplos y problemas de cinemᴩca Vectorial
192…………. Cinemᴩca Vectorial, problemas sacados de parciales

Pag 195 : Resumen de f㲭ulas de Estᴩca y cinemᴩca

FISICA 0
MATEMATICA QUE HAY QUE SABER
PARA ENTENDER FISICA
TEMAS:
FACTOREO – SACAR FACTOR COMUN – PASAR DE TERMINO –
DESPEJAR – SUMAR FRACCIONES – ECUACION DE LA RECTA –
UNA ECUACION CON UNA INCOGNITA – DOS ECUACIONES CON
DOS INCOGNITAS – ECUACION DE UNA PARABOLA – ECUACION
CUADRATICA – SOLUCION DE UNA ECUACIӎ CUADRTICA.

VER
ASIMOV
-2-
FISICA CERO
FISICA 0

F㲭ulas y cosas de matemᴩca que hay que saber para entender f�ca

Hola. A mucha gente le va mal en f�ca por no saber matemᴩca. No es que el tipo no
entienda f�ca. Lo que no entiende es matemᴩca. Entonces cuando le tiran un problema
no sabe para d㮤e agarrar. Si vos sab鳠bien matemᴩca dejᠥste apunte de lado.
Ponete ya mismo a resolver problemas de f�ca, te va a ser m᳠괩l. Si vos sab鳠que la
matemᴩca no te resulta fᣩl, lee con mucha atenci㮠lo que yo pongo acᮠHacete todos
los ejercicios. Hacele preguntas a todos los ayudantes o incluso a m��e encontr᳠por
ah�n algꮠpasillo. Yo s頰erfectamente que nunca nadie te ense᳠nada y ahora te
exigen que sepas todo de golpe. Qu頬e vas a hacer. As�s la cosa.

Ahora, ojo, Todos los temas que pongo acᠳon cosas QUE VAN A APARECER MIEN-
TRAS CURSES LA MATERIA.No es que estoy poniendo cosas descolgadas que nunca
vas a usar. Todo, absolutamente todo lo que figura va a aparecer y vas a tener que usarlo.
Pero:
?
Vas a ver que no es tan dif�l !
ၬegr�
PASAR DE TɒMINO – DESPEJAR

En f�ca todo el tiempo hay que andar despejando y pasando de t鲭ino. Ten鳠que
saberlo a la perfecci㮮 No es dif�l. S㬯 ten鳠que recordar las siguientes reglas:

1 – Lo que estᠳumando pasa restando
2 – Lo que estᠲestando pasa sumando
3 栌o que estᠭultiplicando pasa dividiendo
4 – Lo que estᠤividiendo pasa multiplicando
5 – Lo que estᠣomo 2 pasa como ra�
6 – Lo que estᠣomo ra�pasa como 2
Reglas para pasar
de t鲭ino
Estas reglas se usan para despejar una inc㧮ita de una ecuaci㮮 Despejar x significa
hacer que esta letra inc㧮ita x quede sola a un lado del signo igual. ( Es decir que a la
larga me va a tener que quedar x = tanto ).

X= 25
2 1
2
ASIMOV
-3-
FISICA CERO
Veamos: Usando las reglas de pasaje de t鲭inos despejar X de las siguientes ecuaciones:
1)
2=5昍
X estᠲestando, la paso al otro lado sumando:
El 2 estᠳumando, lo paso al otro lado restando:
2+X=5
X=5沍
2) 4 =
8
X
Por lo tanto ?
x=3
? Soluci㮮
X estᠤividiendo, la paso al otro lado multiplicando: 4.X=8
El cuatro estᠭultiplicando, lo paso al otro miembro dividiendo:
X =
8
4
Es decir:
x=2
? Soluci㮮
3) x2 = 25
La x estᠡl cuadrado. Este cuadrado pasa al otro lado como ra�
Por lo tanto ?
x=5
? Soluci㮮
Resolvete ahora estos ejercicios. En todos hay que despejar X :
1) x + 5 = 8

2) x + 5 = 4
3) 核 栴 = – 7
Rta: x = 3

Rta: x = -1
Rta: x = 3
4)

5)
2
x
2
5x
= 4

= 10
Rta: x =

Rta: x =
1
2
1
25
6)
=
5 – x 5
Rta: x = – 5
7) 淠= 4 – x2
Rta: x =
11
8)
1
(x – 2)2
= 4
Rta: x = 2,5
9)
1
(x – 2)
= a
Rta: x =
1
a
+ 2

3 5
…………
8
+ =
+ =
+ =
? ?
+
+
ASIMOV
-4-
FISICA CERO
10) V =
X – X0
t – t 0
Rta: X = X0 + V (t-t0)
11) Vf =
2gx
Rta: x =
Vf 2
2g
SUMA DE FRACCIONES
Para sumar por ejemplo + lo que hago es lo siguiente:
2 4
Abajo de la raya de fracci㮠va a ir el m�mo comꮠmꬴiplo. Esto quiere decir el nꭥro
m᳠chico que puede ser dividido por 2 y por 4 ( Ese nꭥro ser�4 ). El m�mo comꮍ
mꬴiplo a veces es dif�l de calcular, por eso directamente multiplico los dos nࠤe abajo
y chau. En este caso 2×4 da 8, de manera que en principio el asunto quedar�as�
Para saber lo que va arriba de la raya de fracci㮠uso el siguiente procedimiento:

Haciendo el mismo procedimiento con el 4 de la segunda fracci㮠 me queda:

3 5 12 + 10
2 4 8
Es decir:
Simplificando por dos:
3 5 22
2 4 8
3 5 ?11?
2 4 ? 4 ?
? Resultado
Comprobᠥste asunto con algunas fracciones a ver si aprendiste el m鴯do:
1)
1 1
2 2
Rta : 1
2)
1 1
2 4
Rta :
3
4

+
+
+
+
+
?
ASIMOV
-5-
FISICA CERO
3) 1 +
1
2
Rta :
3
2
4)

5)

6)

7)

8)
1 2
2 3

2 4
3 5

7 5
3 7

1 1
a b

a c
b d
Rta :

Rta :

Rta :

Rta :

Rta :
7
6

22
15

64
21

b+a
a.b

a.d + b.c
b.d
DISTRIBUTIVA
Supon頱ue tengo que resolver esta cuenta: 2 ( 3 + 5 ) = X. Se puede sumar primero lo
que estᠥntre par鮴esis , y en ese caso me quedar�
2(8)=X
16 = X ?Soluci㮮
Pero tambi鮠se puede resolver haciendo distributiva. Eso ser�hacer lo siguiente:

Practicalo un poco con estos ejemplos:
1) 3 ( 4 + 5 )

2) 3 ( 4 栵 )
Rta : 27

Rta : -3

3)
4)
5)
6)
ASIMOV

a(b+c)

a(b+c+d)

a ( m1 + m2 )

堨 m1 g + N2 )
Rta : ab + ac

Rta : ab + ac + ad

Rta : a m1 + a m2

Rta : 堭1 g + 堎2
-6-
FISICA CERO
SACAR FACTOR COMڎ
Sacar factor comꮠes hacer lo contrario de hacer distributiva. Por ejemplo si tengo la
expresi㮺 X = 2 破 + 2 砷 Me va a quedar:
X=2(4+7)
? Saqu頥l 2 como factor comꮍ
A veces en algunos problemas conviene sacar factor comꮠy en otros hacer distributiva.
Eso depende del problema.

Ejemplo: Sacar factor comꮠen las expresiones:
1) F = m1 a + m2 a

2) X = x0 + v t 栶 t0

3) Froz = 堭1 g + 堎2

4) L = F1 d – F2 d
Rta : F = a ( m 1+ m2 )

Rta : X = x0 + v (t-t0)

Rta : 堨 m1 g + N2)

Rta : d ( F1 – F2 )
ECUACIӎ DE UNA RECTA
En matemᴩca la ecuaci㮠de una recta tiene la forma y = m x + b. Se representa en un
par de ejes x – y asi:
y

Y=mx+b

x
En esta ecuaci㮠hay varias que ten鳠que conocer que son:

1
4
4
1,73
ASIMOV
-7-
FISICA CERO
Fijate lo que significa cada una de estas cosas. Veamos primero qu頳on x e y. Si quiero
representar en el plano el punto ( 3 , 2 ) eso significa que:

Veamos ahora qu頥s m. La m representa la pendiente de la recta. La pendiente da una
idea de la inclinaci㮠que tiene la recta. Por ejemplo, la pendiente vale 2/3 eso significa
que la inclinaci㮠de la recta tendrᠱue ser tal que:
m=
2
3
Acᠨay que
avanzar 2

Acᠨay que avanzar 3
m=4
Si la pendiente es 4 puedo poner al Nro 4 como
y me queda:
1
Tengo muchos otros casos. Si la pendiente fuera m = 1 tendr�esto
( Es decir, ser�una recta a 45 ࠩ.
1
1
Si m fuera 1,73, el asunto quedar�as�
1

Entonces, la pendiente de una recta es una funci㮠en donde:

La parte de arriba indica lo que hay que avanzar
11
7
m =
7
11
en Y

La parte de abajo indica lo que hay que avanzar
en X

-1
-1
ASIMOV
-8-
FISICA CERO
Otra cosa: si la pendiente es negativa ( como m = –
7
11
) pongo m =
– 7
11
y la cosa queda:
11
Avanzar 11
Bajar 7
-7
El valor b se llama ordenada al origen y representa el lugar donde la recta corta al eje Y.
Por ejemplo, una recta as�

Otra recta as퍊

Y las rectas que son as퍊 tiene b = – 1

tambi鮠tiene b = -1

tienen b = 0. Es decir, salen del origen de coordenadas.
ӍO SE REPRESENTA UNA RECTA ?
Si tengo una ecuaci㮠y = m x + b y quiero representarla, lo que hago es darle valores a X
y obtener los de Y. Con estos valores formo una tablita y los represento en un par de
ejes x-y. Fijate: Si tengo por ejemplo y = 2 x + 1

Le doy a x el valor 0 y obtengo ? y = 2 . 0 + 1 = 1
Le doy a x el valor 1 y obtengo ? y = 2 . 1 + 1 = 3
Le doy a x el valor 池y obtengo ? y = 2. ( -1 ) + 1 = -1

Puedo tomar todos los valores que quiera pero con tomar 2 alcanza. Poniendo todo esto en
una tabla me queda:
x y
Y=2x+1
0 1
1 3
– 1 -1

Ahora represento los puntos ( 0 ; 1 ) ( 1 ; 3 ) y ( – 1 ; – 1 ) en el plano x-y. Uniendo los
puntos tengo la recta

2
x
1
1
2
ASIMOV
-9-
FISICA CERO
Si quisiera ver si la recta estᠢien trazada puedo fijarme en los valores de m y de b:

La recta corta al eje Y en 1, as�ue estᠢien. Veamos la pendiente:

La pendiente de y = 2 x + 1 es m = 2, as�ue el asunto verifica. Para entender esto mejor
tendr� que hacerte algunos ejercicios. Vamos:

DADA LA ECUACIӎ DE LA RECTA:
a) Ver cu᮴o valen m y b
b) Graficar la recta dᮤole valores de x y sacando los de y
c) Verificar en el grᦩco que los valores de m y b coinciden con los de a)
1) y = x

2) y = x – 1

3) y = 2 – x

4) y = – + 1
2

5) y = 2
Rta: m = 1 , b = 0

Rta : m = 1 , b = -1

Rta: m = – 1 , b = 2

Rta: m = – , b = 1
2

Rta: m = 0 , b = 2
-1
2

2

2
1
1
2
ASIMOV

6) y = 1.000 x + 1
– 10 –

Rta: m = 1.000 , b = 1
Prᣴicamente
son 90͊ FISICA CERO
1
Acᠶan otro tipo de ejercicios que tambi鮠son importantes:

* DADO EL GRFICO, CALCULAR m Y b Y DAR LA ECUACIӎ DE LA RECTA.
a)
1
Rta: m =
1
2
; b=0
y=
1
2
x+0
2
b)
5
Rta: m = –
5
6
; b=5
y= –
5
6
x + 5
6
c)
-1
Rta: m = – 1 ; b = 1
y=-1x+1
d)
-1
Rta: m= –
1
2
; b = -1
y = – x – 1
2
-2

PARBOLA
Una par᢯la es una curva as�
. Desde el punto de vista matemᴩco esta curva
estᠤada por la funci㮺
Y= a x2 + b x + c
? Ecuaci㮍
de la par᢯la
Fijate que si tuviera s㬯 el t鲭ino y = b x + c tendr�una recta. Al agregarle el t鲭ino
con x2 la recta se transforma en una par᢯la. Es el t鲭ino cuadrᴩco el que me dice
que es una par᢯la. Ellos dicen que y = a x2 + b x + c es una funci㮠cuadrᴩca porque
tiene un t鲭ino con x2. Una par᢯la t�ca podr�ser por ejemplo:
Y = 2 x2 + 5 x + 8
En este caso a ser�igual a 2, b a 5 y c ser�8. Los t鲭inos de la ecuaci㮠tambi鮍
pueden ser negativos como en:
Y = – x2 + 2 x -1
Acᠳer�a = – 1, b = 2 y c = -1. A veces el segundo o tercer t鲭ino pueden faltar.
( El primero NO por que es el cuadrᴩco ). Un ejemplo en donde faltan t鲭inos ser�

ASIMOV
– 11 –
FISICA CERO
o tambi鮺
Y= 0,5 x2 栳

Y = x2- 3 x
( a = 0,5 , b = 0, C = -3 )

( a = 1, b = – 3, c = 0 )
La ecuaci㮠tambi鮠puede estar desordenada, entonces para saber qui鮠es a, qui鮠b, y
qui鮠c, tengo que ordenarla primero. Ejemplo:

Y = – 3 x – 1 + 5 x2
( Y = 5 x2 栳 x -1 ?
a = 5, b = – 3, c = – 1)
REPRESENTACIӎ DE UNA PARBOLA
Lo que hago es darle valores a x y sacar los valores de y. Con todos estos valores voy
armando una tabla. Una vez que tengo la tabla, voy representando cada punto en un par
de ejes x,y. Uniendo todos los puntos, obtengo la par᢯la.

De acuerdo a los valores de a, b y c la par᢯la podrᠤar m᳠abierta, m᳠cerrada, m᳍
arriba o m᳠abajo, pero S͠hay una cosa que ten鳠que acordarte y es que si el t鲭ino
cuadrᴩco es negativo la par᢯la va a dar para abajo.
Es decir, por ejemplo, si en el ejemplo anterior hubiese sido Y= – x2 en vez de Y = x2, la
cosa habr�dado as�

or qu頰asa esto ? Rta : Porque a es negativo. ( En este caso a = – 1 )

ASIMOV
12
FISICA CERO
Entonces conviene que te acuerdes siempre que:

Si en la ecuaci㮠Y = a x2 + b x + c el valor de a es
negativo, entonces la par᢯la va a dar para abajo

Dicho de otra manera:

 si a la ecuaci㮠cuadrᴩca no le falta ningꮠt鲭ino ? Rta: No pasa nada, el asunto es
el mismo, lo ꮩco es que va a ser m᳠l�construir la tabla por que hay que hacer m᳍
cuentas. Fijate:

Ejercicios: Representar las siguientes par᢯las y decir cu᮴o valen los t鲭inos a, b y c:

1
ASIMOV
13
FISICA CERO
Soluci㮠de una ecuaci㮠cuadrᴩca
Una ecuaci㮠cuadrᴩca es la ecuaci㮠de una par᢯la igualada a cero. Es decir, si en vez
de tener y = a x2 + b x + c tengo a x2 + b x + c = 0 , eso serᠵna ecuaci㮠cuadrᴩca.
Por ejemplo, son ecuaciones cuadrᴩcas:
X2 + 4 = 0
, 5 X2 栳 X + 7 = 0
, 7 X 栳 X2 = 0
Lo que se busca son los valores de x que satisfagan la ecuaci㮮 u頳ignifica eso ?
Significa reemplazar x por un valor que haga que la ecuaci㮠d頣ero. Supongamos que
tengo:
x2 栴 = 0
頶alores tiene que tomar x para que x2 栴 de cero ? Bueno, a ojo me doy cuenta que
si reemplazo x por 2 la cosa anda. Fijate:
x
22 栴 = 0 ( Se cumple )

brᠡlgꮠotro valor? S�Hay otro valor es x = – 2. Probemos:
(-2)2 栴 = 4 栴 = 0 ( anda )
Este m鴯do de ir probando estᠭuy lindo pero no sirve. or qu頿 Rta: Porque en este
caso funcion㠰or la ecuaci㮠era fᣩl. Pero si te doy la ecuaci㮠0 = – x 2 + 20 x – 30 …
10
mo hac鳿 Acᠮo puede irse probando porque el asunto puede llevarte un aᯠentero.
( Por ejemplo para esa ecuaci㮠las soluciones son: x = 1,51142 y x = 198,4885 ).

A los valores de x que hacen que toda la ecuaci㮠de cero se los llama ra�s de la
ecuaci㮠o soluciones de la ecuaci㮮 Entonces, la idea es encontrar un m鴯do que sirva
para hallar las ra�s de la ecuaci㮮 Este m鴯do ya fue encontrado en el mil seiscientos
y pico y se basa en usar la siguiente f㲭ula ( la demostraci㮠estᠥn los libros ):
X1,2 =
– b ᠠ b 2 – 4ac
2a
Soluci㮠de una
ecuaci㮠cuadrᴩca
㭯 se usa esta f㲭ula ? Mirᠥste ejemplo: Encontrar las ra�s de la ecuaci㮍
Y = x2 栴 x + 3. En este caso a = 1; b =-4 y c = 3. Entonces el choclazo queda:
x1,2 =
– (- 4) ፊ (- 4)2 – 4 籠砳
2 籍

ASIMOV
14
FISICA CERO
? x1,2 =
4 ᠠ 16 – 12
2
? x1,2 =
4 ᠲ
2
x1,2 =
4 ᠠ 4
2
Ahora, para una de las soluciones uso el signo + y para la otra el signo menos. La cosa
queda as�

Entonces x = 3 y x = 1 son las soluciones de la ecuaci㮮

Quiero decirte una cosita m᳠con respecto a este tema: una ecuaci㮠cuadrᴩca podrፊtener una soluci㮬 2 soluciones o ninguna soluci㮮 㭯 es eso ? Fijate: u鍊significa igualar la ecuaci㮠de una par᢯la a cero ? Rta: Bueno, una par᢯la

es esto

Preguntar para qu頶alores de x la y da cero, significa preguntar d㮤e corta la Par᢯la
al eje de las x. Es decir, que las ra�s de una ecuaci㮠cuadrᴩca representan esto:

Soluciones de una ecuaci㮍
cuadrᴩca
Una soluci㮮
Otra soluci㮍
El caso de una soluci㮠ꮩca va a estar dado cuando la par᢯la NO corta al eje de las x
en dos puntos sino que lo corta en un solo punto. Es decir, voy a tener esta situaci㮠:

? Caso de ra�ꮩca.

La ecuaci㮠cuadrᴩca puede no tener soluci㮠cuando la par᢯la No corta en ningꮍ
momento al eje de las x. Por ejemplo:

b 2 – 4ac
?
㍊ ㍊ ASIMOV
15
FISICA CERO
Cuando te toque una ecuaci㮠de este tipo, te vas a dar cuenta porque al hacer
te va a quedar la ra�cuadrada de un nꭥro negativo (como por ejemplo – 4 ). No hay
ningꮠnꭥro que al elevarlo al cuadrado, de negativo, de manera que este asunto no
tiene soluci㮮 Acᠴe pongo algunos ejemplos:
Encontrar las soluciones de la ecuaci㮠usando la f㲭ula x =
( Pod鳠verificar los resultados graficando la par᢯la )
– b ᠠ b 2 – 4ac
2a
1) x2 栲 x 栳 = 0

2) x2 样 x + 12 = 0

3) x2 栲 x + 1 = 0

4) x2 栱8 x + 81

5) x2 + x + 1 = 0

6) x2 核 + 3 = 0
Rta: x1 = 3 ; x2 = -1

Rta: x1 = 4 x2 = 3

Rta: x = 1 ( Ra�doble )

Rta: x = 9 ( Ra�doble )

No tiene soluci㮮

No tiene soluci㮮
SISTEMAS DE 2 ECUACIONES CON 2 INCӇNITAS
Una ecuaci㮠con una inc㧮ita es una cosa as�? x – 3 = 5. Esta ecuaci㮠podr�ser la
ecuaci㮠de un problema del tipo: 㠅ncontrar un nꭥro x tal que si le resto 3 me da 5 䮍
㭯 se resolver�una ecuaci㮠de este tipo ?
Rta: Muy fᣩl. Se despeja x y chau. Fijate :
x泽5
x = 5 + 3 ? x =8
頰asa ahora si me dan una ecuaci㮠as� : x + y = 6 .
Esto es lo que se llama una ecuaci㮠con 2 inc㧮itas. As�omo estᬠno se puede resolver.
O sea, se puede, pero voy a tener infinitas soluciones. Por ejemplo, algunas podr� ser:

x=6; y=0
x=7; y=-1
x=8; y=-2

Creo que ves a d㮤e apunto. Si trato de buscar 2 nꭥros x e y tal que la suma sea 6,
voy a tener millones de soluciones. ( Bueno… millones no… infinitas !!! )

ASIMOV
16
FISICA CERO
Bueno, ahora distinta es la cosa si yo te digo: 㤡me dos nꭥros cuya suma sea 6 y cuya
resta sea 4䠁h�l asunto cambia. Este problema SI tiene soluci㮮 Matemᴩcamente se
pone as�
x +y=6
x-y=4
Esto es lo que ellos llaman sistema de dos ecuaciones con dos inc㧮itas.
mo se resuelve esto? Veamos.

SOLUCIӎ DE UN SISTEMA DE 2 ECUACIONES CON 2 INCӇNITAS
Hay varios m鴯dos para resolver 2 ecuaciones con 2 inc㧮itas. Te recuerdo los 2
m鴯dos m᳠fᣩles. Supongamos que tengo el sistema:
x +y=6
x-y=4
MɔODO 1 : DESPEJAR Y REEMPLAZAR ( SUBSTITUCIӎ )
Se despeja una de las inc㧮itas de la primera ecuaci㮠y se reemplaza en la segunda.
Por ejemplo, despejo x de la 1஠Me queda: x = 6 根.
Reemplazando esta x en la segunda ecuaci㮮 Me queda: ( 6 根 ) 根 = 4
Ahora:
6湭y=4
6洽2y
2 = 2 y ? y=1

Ya calcul頥l valor de y. Reemplazando esta Y en cualquiera de las 2 ecuaciones originales
saco el valor de x. Por ejemplo, si pongo y = 1 en la 1ra de las ecuaciones:

x+1=6

x = 6 栱 ? x=5

MɔODO 2 : SUMA Y RESTA
Se suman o se restan las 2 ecuaciones para que desaparezca alguna de las inc㧮itas.
Por ejemplo:
x +y=6
x-y=4
Sumo las ecuaciones miembro a miembro y me queda:
x+y+x湽6+4

ASIMOV

Ahora la y se va. Me queda:
17

2 x = 10 ? x = 5
FISICA CERO
Al igual que antes, reemplazando este valor de x en cualquiera de las 2 ecuaciones
originales, obtengo el valor de y. Una cosa: Acᠹo sum頬as ecuaciones, pero tambi鮠se
pueden restar.Si las hubiera restado, el asunto hubiera sido el mismo ( se iba a ir la x )
Este segundo m鴯do viene perfecto para los problemas de din᭩ca. El 1er m鴯do
tambi鮠se puede usar, claro. A ellos no les importa qu頭鴯do uses.

Otra cosita: en realidad cada una de las ecuaciones del sistema, es la ecuaci㮠de una
recta. Por ejemplo el sistema anterior se podr�haber puesto as�

ntonces cuᬠser�el significado geom鴲ico de encontrar la soluci㮠de un sistema de
2 ecuaciones con 2 inc㧮itas ? Rta: significa encontrar el punto de encuentro de las 2
rectas. Por ejemplo, en el caso de reci鮠tendr�esto:

Soluci㮠de un sistema de 2
ecuaciones con 2 inc㧮itas

EJERCICIOS
Resolver los siguientes sistemas de 2 ecuaciones con 2 inc㧮itas. ( Pod鳠representar
las 2 rectas para verificar)

ASIMOV
18
FISICA CERO
MATEMTICA CERO 栐ALABRAS FINALES
Acᠴermina mi resumen de matemᴩca. Pero atenci㮬 esta no es toda la
matemᴩca que existe. La matemᴩca es gigantesca. Lo que puse acᠥs lo hiper-
necesario y lo que seguro vas a usar. Hay otros temas que tambi鮠vas a necesitar
como vectores o trigonometr� Estos temas te los voy a ir explicando a lo largo del
libro.
Ahora, pregunta… etest᳠la matemᴩca ?
Rta: Bueno, no sos el ꮩco. El 95 % de la gente la detesta. Es que la matemᴩca es muy
fea. Y encima es dif�l.
ay alguna soluci㮠para esto ?
Rta: Mirᬮ.. no hay salida. Vas a tener que saber matemᴩca s� s�ara entender f�ca.
Y te aclaro, m᳠adelante ES PEOR. A medida que te internes en FISICA O MATEMATICA
vas a tener que saber m᳠matemᴩca, m᳠matemᴩca y m᳠matemᴩca. ( Me refiero a
Anᬩsis I, Anᬩsis II, ᬧebra y dem᳠). Lo ꮩco que se puede hacer para solucionar
esto es estudiar. ( Y estudiar mucho ). Es as�El asunto depende de vos.

FIN MATEMTICA CERO

ASIMOV
– 19 –
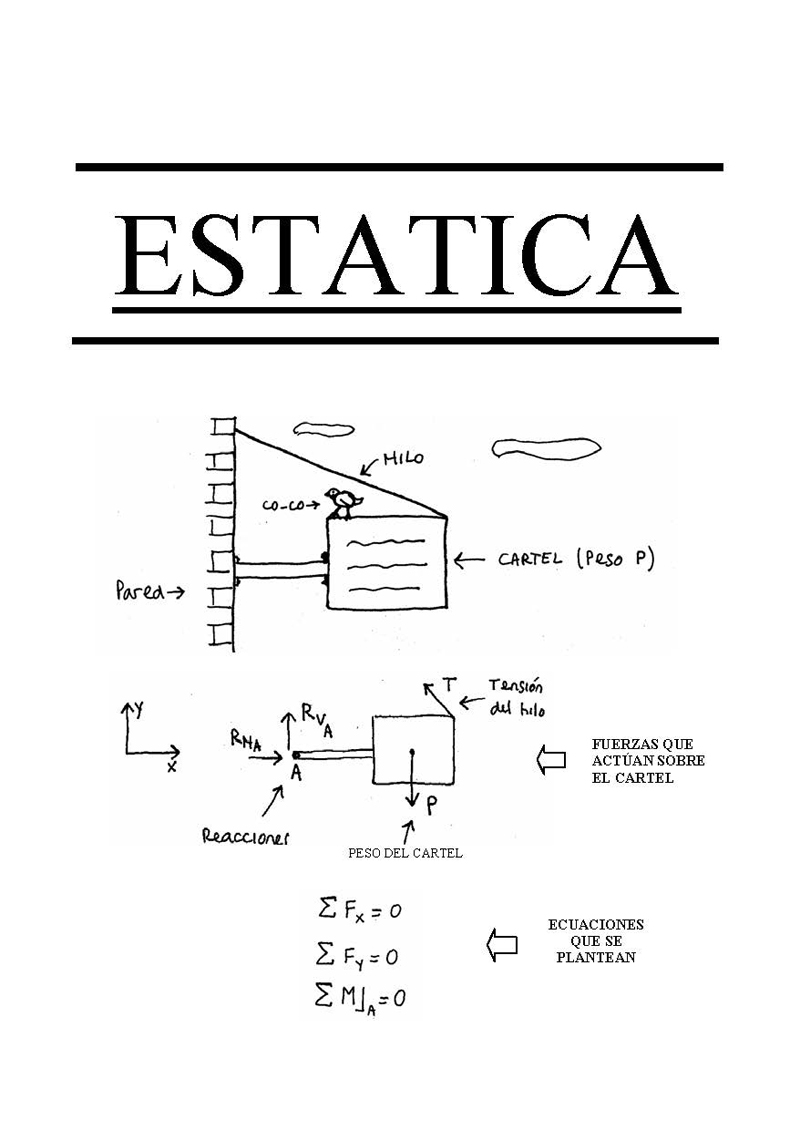
ESTATICA
ESTATICA

FUERZAS QUE
ACTځN SOBRE
EL CARTEL

PESO DEL CARTEL

ECUACIONES
QUE SE
PLANTEAN