
¯ ¯
¯
¯
¯
¯
CORRELACIÓN Y REGRESIÓN CON EXCEL Y GEOGEBRA
Cuando se estudian en forma conjunta dos características (variables estadísticas) de una población o
muestra, se dice que estamos analizando una variable estadística bidimensional. La correlación es el
grado de relación que existe entre ambas características, y la regresión es la forma de expresar
matemáticamente dicha relación.
COEFICIENTE DE CORRELACIÓN DE KARL PEARSON
Llamando también coeficiente de correlación producto-momento.
a) Para datos no agrupados se calcula aplicando la siguiente ecuación:
?? =
? ????
v(? ??2 )(? ??2 )
r = Coeficiente producto-momento de correlación lineal; ?? = ?? – ?? ; ?? = ?? – ??
Ejemplo ilustrativo: Con los datos sobre las temperaturas en dos días diferentes en una ciudad,
determinar el tipo de correlación que existe entre ellas mediante el coeficiente de PEARSON.
X 18 17 15 16 14 12 9 15 16 14 16 18 SX =180
Y 13 15 14 13 9 10 8 13 12 13 10 8 SY= 138
Solución:
Se calcula la media aritmética
??¯ =
? ????
??
Para X:
???? =
180
12
= 15
Para Y:
???? =
138
12
= 11,5
Se llena la siguiente tabla:
??
18
17
15
16
14
12
9
15
16
14
16
18
180
??
13
15
14
13
9
10
8
13
12
13
10
8
138
3
2
0
1
-1
-3
-6
0
1
-1
1
3
?? = ?? – ??
1,5
3,5
2,5
1,5
-2,5
-1,5
-3,5
1,5
0,5
1,5
-1,5
-3,5
?? = ?? – ??
????
9
4
0
1
1
9
36
0
1
1
1
9
72
????
4,5
7
0
1,5
2,5
4,5
21
0
0,5
-1,5
-1,5
-10,5
28
????
2,25
12,25
6,25
2,25
6,25
2,25
12,25
2,25
0,25
2,25
2,25
12,25
63
Se aplica la fórmula:
?? =
? ???? 28
=
v(? ??2 )(? ??2 ) v(72)(63)
= 0,416
Existe una correlación moderada

?? =
En Excel:
En GeoGebra:
El Diagrama de dispersión en Graph:
b) Para datos agrupados, el coeficiente de Correlación de Pearson se calcula aplicando la
siguiente fórmula:
?? · ? ?? · ???? · ???? – (? ???? · ????) (? ???? · ????)
v[?? · ? ???? · ????2 – (? ???? · ????)2 ][?? · ? ???? · ???? 2 – (? ???? · ????)2 ]
Donde:
?? = número de datos; ?? = frecuencia de celda; ???? = frecuencia de la variable X; ???? = frecuencia de la
variable Y; ???? = valores codificados o cambiados para los intervalos de la variable X, procurando que
al intervalo central le corresponda ???? = 0, para que se hagan más fáciles los cálculos; ???? = valores
codificados o cambiados para los intervalos de la variable X, procurando que al intervalo central le
corresponda ???? = 0, para que se hagan más fáciles los cálculos.
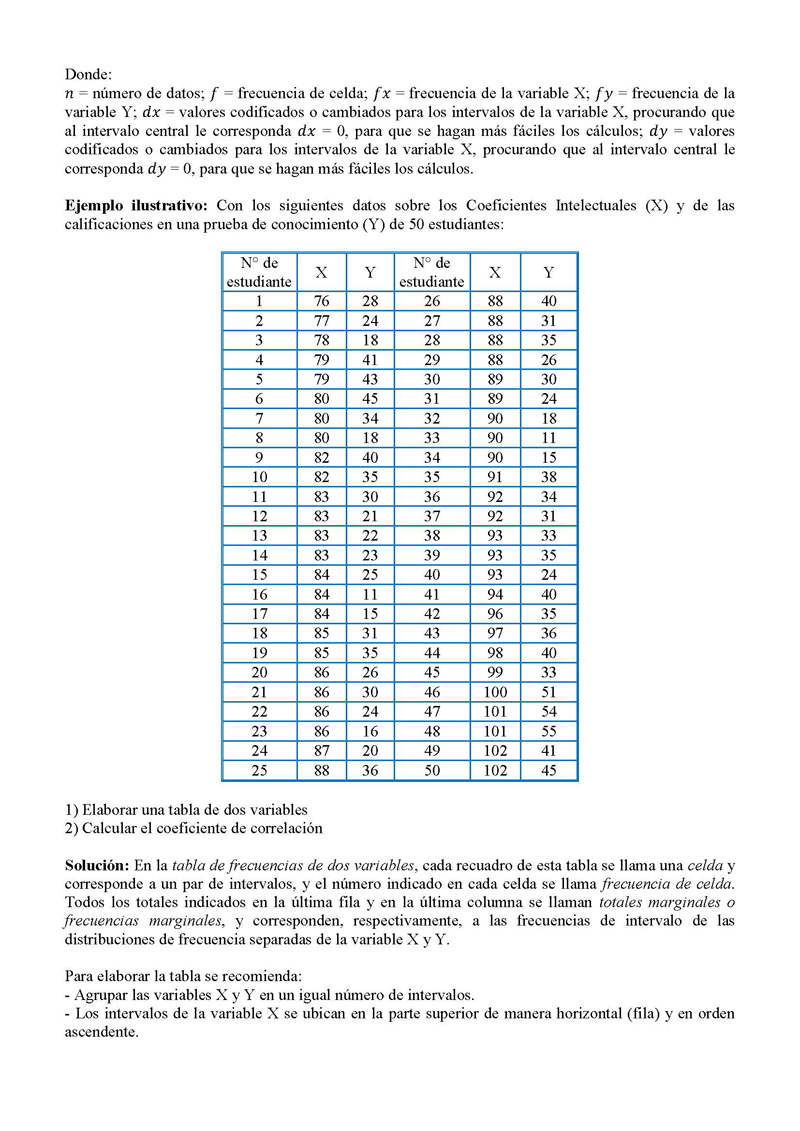
Ejemplo ilustrativo: Con los siguientes datos sobre los Coeficientes Intelectuales (X) y de las
calificaciones en una prueba de conocimiento (Y) de 50 estudiantes:
N° de
estudiante
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
X
76
77
78
79
79
80
80
80
82
82
83
83
83
83
84
84
84
85
85
86
86
86
86
87
88
Y
28
24
18
41
43
45
34
18
40
35
30
21
22
23
25
11
15
31
35
26
30
24
16
20
36
N° de
estudiante
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
X
88
88
88
88
89
89
90
90
90
91
92
92
93
93
93
94
96
97
98
99
100
101
101
102
102
Y
40
31
35
26
30
24
18
11
15
38
34
31
33
35
24
40
35
36
40
33
51
54
55
41
45
1) Elaborar una tabla de dos variables
2) Calcular el coeficiente de correlación
Solución: En la tabla de frecuencias de dos variables, cada recuadro de esta tabla se llama una celda y
corresponde a un par de intervalos, y el número indicado en cada celda se llama frecuencia de celda.
Todos los totales indicados en la última fila y en la última columna se llaman totales marginales o
frecuencias marginales, y corresponden, respectivamente, a las frecuencias de intervalo de las
distribuciones de frecuencia separadas de la variable X y Y.
Para elaborar la tabla se recomienda:
– Agrupar las variables X y Y en un igual número de intervalos.
– Los intervalos de la variable X se ubican en la parte superior de manera horizontal (fila) y en orden
ascendente.

Calificaciones(Y)
– Los intervalos de la variable Y se ubican en la parte izquierda de manera vertical (columna) y en
orden descendente.
Para elaborar los intervalos se procede a realizar los cálculos respectivos:
En la variable X:
Calculando el Rango se obtiene:
?? = ????á?? – ????í?? = 102 – 76 = 26
Calculando el número de intervalos se obtiene:
???? = 1 + 3,32 · ??????(??) = 1 + 3,32 · ??????50 = 6,6 = 7
Calculando el ancho se obtiene:
?? 26
?? = =
???? 6,6
= 3,93 = 4
En la variable Y:
Calculando el Rango se obtiene:
?? = ????á?? – ????í?? = 55 – 11 = 44
Calculando el número de intervalos se obtiene:
???? = 1 + 3,32 · ??????(??) = 1 + 3,32 · ??????50 = 6,64 = 7
Calculando el ancho se obtiene:
?? 44
?? = =
???? 6,64
= 6,62 = 7
Nota: Para la variable X se tomará un ancho de intervalo igual a 4 y para la variable Y un ancho de
intervalo igual a 7. Debe quedar igual número de intervalos para cada variable, que en este ejemplo es
igual a 7.
Contando las frecuencias de celda para cada par de intervalos de las variables X y Y se obtiene la
siguiente tabla de frecuencias de dos variables:
Coeficientes Intelectuales (X)
53-59
46-52
76-79
80-83 84-87 88-91 92-95 96-99 100-103
2
1
????
2
1
39-45
32-38
25-31
18-24
2
1
2
2
2
1
4
1
4
2
1
3
3
2
1
3
1
1
1
3
2
9
12
10
11
11-17
3
2
5
????
5
9
10
11
6
4
5
50
Interpretación:
– El número 2 es la frecuencia de la celda correspondiente al par de intervalos 76-79 en Coeficiente
Intelectual y 39-45 en Calificación obtenida en la prueba de conocimiento.
– El número 5 en la fila de ???? es el total marginal o frecuencia marginal del intervalo 76-79 en
Coeficiente Intelectual.
– El número 2 en la columna de ???? es el total marginal o frecuencia marginal del intervalo 53-59 en
Calificación obtenida en la prueba de conocimiento.
– El número 50 es total de frecuencias marginales y representa al número total de estudiantes.

Calificaciones(Y)
2) Realizando los cálculos respectivos se obtiene la siguiente tabla:
Coeficientes Intelectuales (X)
76-79 80-83 84-87 88-91 92-95 96-99 100-103
????
-3
-2
-1
0
1
2
3
???? ???? · ???? ???? · ???? 2 ?? · ???? · ????
????
53-59
46-52
3
2
2
1
18
6
2
1
6
2
18
4
18
6
39-45
32-38
25-31
18-24
1
0
-1
-2
2
1
2
-6
3
12
2
2
1
4
-4
0
2
16
1
4
2
0
4
4
1
3
3
2
0
0
0
0
1
3
1
1
1
0
-1
-2
1
3
2
0
2
6
9
12
10
11
9
0
-10
-22
9
0
10
44
-1
0
8
30
11-17
-3
3
9
2
0
5
-15
45
9
????
5
9
10
11
6
4
5
50
-30
130
70
???? · ????
???? · ???? 2
?? · ???? · ????
-15
45
9
-18
36
14
-10
10
17
0
0
0
6
6
-2
8
16
2
15
45
30
-14
158
70
Nota:
Los números de las esquinas de cada celda en la anterior tabla representan el producto
?? · ???? · ????, así por ejemplo, para obtener el número el número -6 de los intervalos 76-79 en X y 39-45
en Y se obtiene multiplicando 2·(-3)·1 = -6. Para obtener el número 18 de los intervalos 100-103 en X
y 53-59 en Y se obtiene multiplicando 2·3·3 = 18
-Los números de la última columna (18, 6, -1, 0, 8, 30 y 9) se obtienen sumando los números de las
esquinas en cada fila, así por ejemplo, para obtener el número -1 se suma (-6) + (-4) + 0 + 1 +2 + 6 = -1
-Los números de la última fila (9, 14, 17, 0, -2, 2 y 30) se obtienen sumando los números de las
esquinas en cada columna, así por ejemplo, para obtener el número 9 se suma (-6) + 3 + 12 = 9.
-Para obtener el número -30 de la antepenúlmina columna se obtiene sumando los resultados de ???? ·
????, es decir, representa la ? ???? · ????
-Para obtener el número -14 de la antepenúlmina fila se obtiene sumando los resultados de ???? · ????, es
decir, representa la ? ???? · ????
-Para obtener el número 130 de la penúltima columna se obtiene sumando los resultados de ???? · ????2 ,
es decir, representa ? ???? · ???? 2
-Para obtener el número 158 de la penúltima fila se obtiene sumando los resultados de ???? · ????2 , es
decir, representa ? ???? · ????2
-Para obtener último número 70 de la última columna se obtiene sumando los resultados de la última
columna 18 +6 +(-1) +0 + 8 + 30 +9 = 70, es decir, representa ? ???? · ???? · ????
-Para obtener último número 70 de la última fila se obtiene sumando los resultados de la última fila
9 + 14 + 17 + 0 +(-2) +2 + 30 = 70 , es decir, representa ? ???? · ???? · ???? . Por lo tanto tiene que ser igual
al último número de la última columna como comprobación que los cálculos de la tabla han sido
correctos.
Observando los datos en la tabla anterior se remplaza los valores en la ecuación del Coeficiente de
Correlación de Pearson para datos agrupados, obteniéndose:

?? =
=
=
2
?? · ? ?? · ???? · ???? – (? ???? · ????) (? ???? · ????)
v[?? · ? ???? · ????2 – (? ???? · ????)2 ][?? · ? ???? · ???? 2 – (? ???? · ????)2 ]
?? =
?? =
50 · 70 – (-14)(-30)
v[50 · 158 – (-14)2 ][50 · 130 – (-30)2 ]
3080 3080
=
= 0,469
v43142400 6568,287448
3500 – 420
v[7900 – 196][6500 – 900]
3080
v[7704][5600]
Existe una correlación positiva moderada
COEFICIENTE DE CORRELACIÓN POR RANGOS DE SPEARMAN
Este coeficiente se emplea cuando una o ambas escalas de medidas de las variables son ordinales, es
decir, cuando una o ambas escalas de medida son posiciones. Ejemplo: Orden de llegada en una carrera
y peso de los atletas. Se calcula aplicando la siguiente ecuación:
???? = 1 –
6 ? ??2
??(??2 – 1)
???? = Coeficiente de correlación por rangos de Spearman;d = Diferencia entre los rangos (X menos Y)
n = número de datos
Ejemplo ilustrativo N° 1: La siguiente tabla muestra el rango u orden obtenido en la primera
evaluación (X) y el rango o puesto obtenido en la segunda evaluación (Y) de 8 estudiantes
universitarios en la asignatura de Estadística. Calcular el coeficiente de correlación por rangos de
Spearman.
Estudiante ?? ??
Dyanita
Elizabeth
Mario
Orlando
Mathías
Josué
Emily
1 3
2 4
3 1
4 5
5 6
6 2
7 8
Monserrath 8 7
Para calcular el coeficiente de correlación por rangos de Spearman de se llena la siguiente tabla:
Estudiante ?? ?? ?? = ?? – ?? ??2 = (?? – ??)2
Dyanita
Elizabeth
Mario
Orlando
Mathías
Josué
Emily
1 3
2 4
3 1
4 5
5 6
6 2
7 8
-2
-2
2
-1
-1
4
-1
4
4
4
1
1
16
1
Monserrath 8 7
1
1
S?? = 32
Se aplica la fórmula:
???? = 1 –
6 ? ??2
??(??2 – 1)
= 1-
6 · 32
8(82 – 1)
=1-
192 504 – 192 312
= =
504 504 504
= 0,619
Por lo tanto existe una correlación positiva moderada entre la primera y segunda evaluación de los 8
estudiantes.

En Excel:
En GeoGebra:
Ejemplo ilustrativo N° 2: La siguiente tabla muestra las calificaciones de 8 estudiantes universitarios
en las asignaturas de Matemática y Estadística. Calcular el coeficiente de correlación por rangos de
Spearman.
N° Estudiante Matemática Estadística
1 Dyana
2 Elizabeth
3 Mario
4 Orlando
5 Mathías
6 Josué
7 Emily
8 Monserrath
10
9
8
7
7
6
6
4
8
6
10
9
8
7
6
9
Solución:
Para calcular el coeficiente de correlación por rangos de Spearman se procede a clasificar u ordenar los
datos en rangos (X para Matemática y Y para Estadística) tomando en cuenta las siguientes
observaciones:
En la asignatura de Matemática se observa:
– Dyana tiene la más alta calificación, ocupando el primer puesto, por lo que su rango es 1
– Elizabeth ocupa el segundo puesto, por lo que su rango es 2
– Mario se encuentra ubicado en el tercer lugar, por lo que su rango es 3
– Orlando y Mathías ocupan el cuarto y quinto puesto, por lo que su rango es la media aritmética de 4 y
5 que da por resultado 4,5
– Josué y Emily ocupan el sexto y séptimo lugar, por lo que su rango es la media aritmética de 6 y 7 que
da por resultado 6,5
– Monserrath se encuentra ubicada en el octavo lugar, por lo que su rango es 8
En la asignatura de Estadística se observa:
– Mario tiene la más alta calificación, ocupando el primer puesto, por lo que su rango es 1
– Orlando y Monserrath ocupan el segundo y tercer puesto, por lo que su rango es la media aritmética
de 2 y 3 que da por resultado 2,5

??
??
¯ ¯
– Dyana y Mathías ocupan el cuarto y quinto puesto, por lo que su rango es la media aritmética de 4 y 5
que da por resultado 4,5
– Josué se encuentra ubicado en el sexto lugar, por lo que su rango es 6
– Elizabeth y Emily ocupan el séptimo y octavo lugar, por lo que su rango es la media aritmética de 7 y
8 que da por resultado 7,5
Los rangos X y Y se presentan en la siguiente tabla:
N° Estudiante Matemática Estadística
??
??
1 Dyana
2 Elizabeth
3 Mario
4 Orlando
5 Mathías
6 Josué
7 Emily
8 Monserrath
10
9
8
7
7
6
6
4
8
6
10
9
8
7
6
9
1
2
3
4,5
4,5
6,5
6,5
8
4,5
7,5
1
2,5
4,5
6
7,5
2,5
Calculando ??, ??2 ?? S??2 se obtiene los siguientes resultados:
N° Estudiante Matemática Estadística
?? = ?? – ?? ??2
= (?? – ??)2
1 Dyana
2 Elizabeth
3 Mario
4 Orlando
5 Mathías
6 Josué
7 Emily
8 Monserrath
10
9
8
7
7
6
6
4
8
6
10
9
8
7
6
9
1
2
3
4,5
4,5
6,5
6,5
8
4,5
7,5
1
2,5
4,5
6
7,5
2,5
-3,5
-5,5
2
2
0
0,5
-1
5,5
12,25
30,25
4
4
0
0,25
1
30,25
S d2 = 82
Aplicando la fórmula se obtiene:
???? = 1 –
6 ? ??2
??(??2 – 1)
= 1-
6 · 82
8(82 – 1)
=1-
492 504 – 492
=
504 504
=
12
504
= 0,024
COEFICIENTE DE DETERMINACIÓN
Revela qué porcentaje del cambio en Y se explica por un cambio en X. Se calcula elevando al cuadrado
el coeficiente de correlación.
?? =
? ????
v(? ??2 )(? ??2 )
?? = ?? – ??; ?? = ?? – ??; r = Coeficiente de correlación de Pearson; ?? 2 = Coeficiente de determinación
La ecuación del coeficiente producto-momento (Coeficiente de Pearson) ?? =
escribirse en la forma equivalente:
?? ? ???? – (? ??)(? ??)
?????????????????????? ???? ?????????????? = ?? =
v[?? ? ??2 – (? ??)2 ][?? ? ??2 – (? ??)2 ]
? ????
v(? ?? 2)(? ?? 2)
puede
De donde coeficiente de determinación = ?? 2 = (Coeficiente de Pearson )2
Ejemplo ilustrativo: Con los datos de la siguiente tabla sobre las temperaturas, calcular el coeficiente
de determinación empleando la ecuación obtenida de la forma equivalente del coeficiente de Pearson.
X 18 17 15 16 14 12 9 15 16 14 16 18
Y 13 15 14 13 9 10 8 13 12 13 10 8

?? =
=
Solución:
Se calcula el coeficiente de Pearson llenando la siguiente tabla:
??
18
17
15
16
14
12
9
15
16
14
16
18
??
13
15
14
13
9
10
8
13
12
13
10
8
????
234
255
210
208
126
120
72
195
192
182
160
144
????
324
289
225
256
196
144
81
225
256
196
256
324
????
169
225
196
169
81
100
64
169
144
169
100
64
???? = ?????? ???? = ?????? ?????? = ???????? ?????? = ????????
Se aplica la ecuación para calcular el coeficiente de Pearson.
?????? = ????????
?? ? ???? – (? ??)(? ??)
v[?? ? ??2 – (? ??)2 ][?? ? ??2 – (? ??)2 ]
12 · 2098 – 180 · 138
v[12 · 2772 – (180)2 ][12 · 1650 – (138)2 ]
?? =
25176 – 24840
v[33264 – 32400][19800 – 19044]
=
336
v[864][756]
=
336
v653184
=
336
808,198
= 0,4157
Elevando al cuadrado coeficiente de Pearson queda calculado el coeficiente de determinación.
Coeficiente de determinación = ?? 2 = (0,4157)2 = 0,1728
Esto establece que 17,28% del cambio en Y se explica mediante un cambio en X.
Nota: El ?? 2 tiene significado sólo para las relaciones lineales. Dos variables pueden tener ?? 2 = 0 y sin
embargo estar relacionadas en sentido curvilíneo. El valor de ?? 2 no se interpreta como si la variable Y
fuera causado por un cambio de la variable X, ya que la correlación no significa causa.
ANÁLISIS DE REGRESIÓN
La regresión examina la relación entre dos variables, pero restringiendo una de ellas con el objeto de
estudiar las variaciones de una variable cuando la otra permanece constante. En otras palabras, la
regresión es un método que se emplea para predecir el valor de una variable en función de valores
dados a la otra variable.
a) LA RECTA DE LOS MÍNIMOS CUADRADOS
Se llama línea de mejor ajuste y se define como la línea que hace mínima la suma de los cuadrados de
las desviaciones respecto a ella de todos los puntos que corresponden a la información recogida.
La recta de los mínimos cuadrados que aproxima el conjunto de puntos
(??1 , ??1 ), (??2 , ??2 ), (??3 , ??3 ), … … (???? , ???? ) tomando en cuenta a Y como variable dependiente tiene por
ecuación
?? = ??0 + ??1 ??

{
?x
{
¯ ¯
?y
¯ ¯
¯ ¯
A esta ecuación suele llamarse recta de regresión de ?? sobre ??, y se usa para estimar los valores de ??
para valores dados de ??
Si a la recta de regresión ?? = ??0 + ??1 ?? se le suma en ambos lados ? ?? = ?(??0 + ??1 ??) se obtiene
? ?? = ??0 ?? + ??1 ? ??
Si a la recta de regresión ?? = ??0 + ??1 ?? se multiplica por ?? a ambos lados y luego se suma
? ?? ?? = ? ??(??0 + ??1 ??) se obtiene ? ?? ?? = ??0 ? ?? + ??1 ? ??2
Las constantes ??0 ?? ??1 quedan fijadas al resolver simultáneamente las ecuaciones anteriormente
encontradas, es decir, al resolver el siguiente sistema de ecuaciones:
S?? = ??0 ?? + ??1 S??
S???? = ??0 S?? + ??1 S??2
Que se llaman las ecuaciones normales para la recta de mínimos cuadrados.
Las constantes ??0 y ??1 de las anteriores ecuaciones también se pueden calcular empleando las
siguientes fórmulas:
??0 =
? ?? · ? ??2 – ? ?? · ? ????
?? ? ??2 – (? ??)2
??1 =
?? ? ???? – ? ?? · ? ??
?? ? ??2 – (? ??)2
Otra ecuación para los mínimos cuadrados para ?? = ?? – ?? , ?? = ?? – ?? de la recta de regresión de Y
sobre X es:
? ????
?? = ( 2 ) ??
La recta de los mínimos cuadrados que aproxima el conjunto de puntos
(??1 , ??1 ), (??2 , ??2 ), (??3 , ??3 ), … … (???? , ???? ) tomando en cuenta a X como variable dependiente tiene por
ecuación:
?? = ??0 + ??1 ??
A esta ecuación suele llamarse recta de regresión de X sobre Y, y se usa para estimar los valores de X
para valores dados de Y. Las constantes ??0 y ??1 quedan fijadas al resolver el siguiente sistema de
ecuaciones:
S?? = ??0 ?? + ??1 S??
S???? = ??0 S?? + ??1 S??2
Las constantes ??0 y ??1 del sistema de ecuaciones anterior se pueden calcular empleando las siguientes
fórmulas:
??0 =
? ?? · ? ??2 – ? ?? · ? ????
?? ? ??2 – (? ??)2
??1 =
?? ? ???? – ? ?? · ? ??
?? ? ??2 – (? ??)2
Otra ecuación para los mínimos cuadrados para ?? = ?? – ?? , ?? = ?? – ?? es:
? ????
?? = ( 2 ) ??
El punto de intersección entre las rectas ?? = ??0 + ??1 ?? con ?? = ??0 + ??1 ?? se simboliza (??, ??) y se
llama centroide o centro de gravedad

{
?x
{
{
=
=
=
|
|
=
=
=
Ejemplo ilustrativo: Con los datos de la siguiente tabla sobre la altura en centímetros (X) y los pesos
en kilogramos (Y) de una muestra de 8 estudiantes varones tomada al azar del segundo semestre de una
universidad.
X 152 157 162 167 173 178 182 188
Y 56 61 67 72 70 72 83 92
1) Ajustar la recta de mínimos cuadrados para Y como variable dependiente resolviendo el sistema:
S?? = ??0 ?? + ??1 S??
S???? = ??0 S?? + ??1 S??2
2) Ajustar la recta de mínimos cuadrados para Y como variable dependiente empleando las fórmulas:
??0 =
? ?? · ? ??2 – ? ?? · ? ????
?? ? ??2 – (? ??)2
??1 =
?? ? ???? – ? ?? · ? ??
?? ? ??2 – (? ??)2
3) Ajustar la recta de mínimos cuadrados para Y como variable dependiente empleando la fórmula:
? ????
?? = ( 2 ) ??
4) Ajustar la recta de mínimos cuadrados para X como variable dependiente resolviendo el sistema:
S?? = ??0 ?? + ??1 S??
S???? = ??0 S?? + ??1 S??2
5) Calcular el punto centroide.
6) Elaborar el diagrama de dispersión. Y en el mismo diagrama graficar las dos rectas de mínimos
cuadrados obtenidas en los pasos anteriores.
7) Estimar el valor de Y cuando X = 200 en el diagrama de dispersión de Y como variable dependiente.
8) Estimar el valor de X cuando Y= 100 en el diagrama de dispersión X como variable dependiente.
Solución: Se llena la siguiente tabla:
??
152
157
162
167
173
178
182
188
??
56
61
67
72
70
72
83
92
????
8512
9577
10854
12024
12110
12816
15106
17296
??2
23104
24649
26244
27889
29929
31684
33124
35344
??2
3136
3721
4489
5184
4900
5184
6889
8464
S?? = 1359 S?? = 573 S???? = 98295 S??2 = 231967 S??2 = 41967
1) Remplazando valores en el sistema se tiene:
S?? = ??0 ?? + ??1 S??
S???? = ??0 S?? + ??1 S??
573 = ??0 · 8 + ??1 · 1359 8??0 + 1359??1 = 573
2 ? 98295 = ??0 · 1359 + ??1 · 231967 ? {1359??0 + 231967??1 = 98295
Resolviendo el sistema por determinantes (regla de Cramer) se obtiene:
??0 =
573 1359
???0 |98295 231967| 573 · 231967 – 98295 · 1359 -665814
? 8 1359 8 · 231967 – 1359 · 1359 8855
1359 231967
= -75,191
??1 =
8 573
???1 |1359 98295| 8 · 98295 – 1359 · 573 7653
? 8855 8855 8855
= 0,864

¯
¯
Para calcular los valores de ??1 ?? ??0 en Excel se calcula de la siguiente manera:
Los cálculos en GeoGebra se muestran en la siguiente figura:
Remplazando valores en la ecuación respectiva se obtiene:
?? = ??0 + ??1 ?? ? ?? = -75,191 + 0,864??
Interpretación:
– El valor ??1 = 0,864 indica que la recta tiene una pendiente positiva aumentando a razón de 0,864
– El valor de ??0 = -75,191 indica el punto en donde la recta interseca al eje Y cuanto X = 0
2) Con los datos de la tabla anterior se substituye valores en las siguientes ecuaciones:
??0 =
? ?? · ? ??2 – ? ?? · ? ???? 573 · 231967 – 1359 · 98295 -665814
= =
?? ? ??2 – (? ??)2 8 · 231967 – (1359)2 8855
– 75,191
??1 =
?? ? ???? – ? ?? · ? ?? 8 · 98295 – 1359 · 573 7653
= =
?? ? ??2 – (? ??)2 8 · 231967 – (1359)2 8855
= 0,864
Remplazando valores en la ecuación respectiva se obtiene:
?? = ??0 + ??1 ?? ? ?? = -75,191 + 0,864??
3) Se calcula las medias aritméticas de X y Y para llenar la siguiente tabla:
?? =
1359
8
= 169,875 ; ?? =
573
8
= 71,625

¯
¯
?x
¯
¯
{
{
¯ ¯
¯ ¯
??
152
157
162
167
173
178
182
188
??
56
61
67
72
70
72
83
92
-17,88
-12,88
-7,875
-2,875
3,125
8,125
12,125
18,125
?? = ?? – ??
?? = ?? – ??
-15,625
-10,625
-4,625
0,375
-1,625
0,375
11,375
20,375
????
279,297
136,797
36,422
-1,078
-5,078
3,047
137,922
369,297
?? 2
319,516
165,766
62,016
8,266
9,766
66,016
147,016
328,516
?? 2
244,141
112,891
21,391
0,141
2,641
0,141
129,391
415,141
S?? = 1359
S?? = 573
S???? = 956,625 S?? 2 = 1106,875 S?? 2 = 925,875
Remplazando valores en la fórmula respectiva se obtiene:
? ????
?? = ( 2 ) ?? ? ?? =
956,625
1106,875
?? ? ?? – ?? =
956,625
1106,875
(?? – ??)
?? – 71,625 =
956,625
1106,875
(?? – 169,875) ? 1106,875(?? – 71,625) = 956,625(?? – 169,875)
1106,875?? – 79280,20838 = 956,625?? – 162510,4984
1106,875?? = 956,625?? – 162510,4984 + 79280,20838
1106,875?? = 956,625?? – 83230,29
?? =
956,625?? – 83230,29
1106,875
? ?? =
956,625?? 83230,29
–
1106,875 1106,875
? ?? = 0,864?? – 75,19
?? = -75,19 + 0,864??
4) Remplazando valores en sistema respectivo se obtiene:
S?? = ??0 ?? + ??1 S??
S???? = ??0 S?? + ??1 S??
1359 = ??0 · 8 + ??1 · 573 8??0 + 573??1 = 1359
2 ? 98295 = ??0 · 573 + ??1 · 41967 ? 573??0 + 41967??1 = 98295
Resolviendo el sistema se obtiene:
??0 = 95,871; ??1 = 1,033
Remplazando valores en la ecuación de la recta de mínimos cuadrados se obtiene:
?? = ??0 + ??1 ?? ? ?? = 95,871 + 1,033??
Los cálculos en GeoGebra insertando Ajuste Lineal se muestran en la siguiente figura:
Interpretación:
– El valor ??1 = 1,033 indica que la recta tiene una pendiente positiva aumentando a razón de 1,033
– El valor de ??0 = 95,871 indica el punto en donde la recta interseca al eje X cuanto Y = 0
5) Para calcular el centroide (??, ??) se resuelve el sistema formado por las dos rectas de los mínimos
cuadrados en donde X es ?? y Y es ??.
?? = -75,191 + 0,864??
?? = 95,871 + 1,033??
Al resolver el sistema se obtiene el centroide: X = 169,3 y Y = 71,092

2
Año
6) Empleando el programa Graph se obtiene la siguiente figura:
7) Remplazando X = 200 en la ecuación solicitada se obtiene:
?? = -75,191 + 0,864?? = -75,191 + 0,864 · 200 = -75,191 + 172,8 = 97,609
8) Remplazando Y = 100 en la ecuación solicitada se obtiene:
?? = 95,871 + 1,033?? = ?? = 95,871 + 1,033 · 100 = ?? = 95,871 + 103,3 = 199,171
b) LA PARÁBOLA DE LOS MÍNIMOS CUADRADOS
La
parábola
de
mínimos
cuadrados
que
aproxima
el
conjunto
de
puntos
(??1 , ??1 ), (??2 , ??2 ), (??3 , ??3 ), … (???? , ???? ) tiene ecuación dada por ?? = ??0 + ??1 ?? + ??2 ?? , donde las
constantes ??0 , ??1 y ??2 se determinan al resolver simultáneamente el sistema de ecuaciones que se
forma al multiplicar la ecuación ?? = ??0 + ??1 ?? + ??2 ??2 por 1, ??, ?? sucesivamente, y sumando después.
S?? = ??0 ?? + ??1 S?? + ??2 S??2
{ S???? = ??0 S?? + ??1 S??2 + ??2 S??3
S??2 ?? = ??0 S??2 + ??1 S??3 + ??2 S??4
Ejemplo ilustrativo: La siguiente tabla muestra la población de un país en los años 1960-2010 en
intervalos de 5 años.
196019651970 197519801985 1990 1995 2000 2005 2010
Población (millones) 4,52 5,18 6,25 7,42 8,16 9,12 10,9211,6212,68 13,1213,97
1) Ajustar una parábola de mínimos cuadrados de la forma ?? = ??0 + ??1 ?? + ??2 ??2
2) Calcular los valores de tendencia para los años dados.
3) Estimar la población para los años 2015 y 2020.
4) Elaborar un diagrama de dispersión, y en el mismo diagrama graficar la parábola de los mínimos
cuadrados.
Nota: Se recomienda codificar o cambiar la numeración de los años, tratando que X = 0 esté ubicado
en lo posible en el centro.

{
|
|
|
|
|
|
Solución: Para ajustar una parábola de mínimos cuadrados se llena la siguiente tabla:
Año
1960
1965
1970
1975
1980
1985
1990
1995
2000
2005
2010
S
??
-5
-4
-3
-2
-1
0
1
2
3
4
5
0
??
4,52
5,18
6,25
7,42
8,16
9,12
10,92
11,62
12,68
13,12
13,97
102,96
??2
25
16
9
4
1
0
1
4
9
16
25
110
??3
-125
-64
-27
-8
-1
0
1
8
27
64
125
0
??4
625
256
81
16
1
0
1
16
81
256
625
1958
????
-22,6
-20,72
-18,75
-14,84
-8,16
0
10,92
23,24
38,04
52,48
69,85
109,46
??2 ??
113
82,88
56,25
29,68
8,16
0
10,92
46,48
114,12
209,92
349,25
1020,66
Se remplaza valores en el sistema y se obtiene:
S?? = ??0 ?? + ??1 S?? + ??2 S??2
{ S???? = ??0 S?? + ??1 S??2 + ??2 S??3
S??2 ?? = ??0 S??2 + ??1 S??3 + ??2 S??4
102,96 = a0 · 11 + a1 · 0 + a2 · 110
11a0 + 0a1 + 110a2 = 102,96
109,46 = a0 · 0 + a1 · 110 + a2 · 0 ? { 0a0 + 110a1 + 0a2 = 109,46
1020,66 = a0 · 110 + a1 · 0 + a2 · 1958
110a0 + 0a1 + 1958a2 = 1020,66
Resolviendo el sistema empleando determinantes (regla de Cramer) se obtiene:
102,96
0
110
???? =
???0
?
=
102,96 0
| 109,46 110
1020,66 0
11 0
| 0
110
110
0
110
0 |
1958
110
0 |
1958
=
109,46 110
|1020,66 0
102,96 0
109,46 110
11 0
0
110
|110
0
11
0
0
1958|
110
0
110
0
1958|
110
0
110
0
a0 =
22175524,8 + 0 + 0 – 12349986 – 0 – 0 9825538,8
=
2369180 + 0 + 0 – 1331000 – 0 – 0 1038180
= 9,464
11
102,96
110
??1 =
???1
?
=
11
| 0
110
102,96 110
109,46 0 |
1020,66 1958
1038180
=
0
|110
11
0
109,46 0
1020,66 1958|
102,96 110
109,46 0
1038180
??1 =
23577549,48 + 0 + 0 – 1324466 – 0 – 0 2357549,48
=
1038180 1038180
= 0,995

|
|
11
0
102,96
??2 =
???2
?
=
11
| 0
110
0 102,96
110 109,46 |
0 1020,66
1038180
=
0
|110
11
0
110 109,46
0 1020,66|
0 102,96
110 109,46
1038180
??2 =
1234998,6 + 0 + 0 – 1245816 – 0 – 0 -10817,4
=
1038180 1038180
= -0,01
El sistema de ecuaciones resuelto en GeoGebra:
67669
7150
= 9,464 ;
5473
5500
= 0,995 ; –
149
14300
= -0,01
Remplazando los valores encontrados se obtiene la ecuación de la parábola de mínimos cuadrados:
?? = ??0 + ??1 ?? + ??2 ??2 ? ?? = 9,464 + 0,995?? – 0,01??2
2) Los valores de tendencia se obtienen al remplazar los valores de X en la ecuación de la parábola de
mínimos cuadrados, los cuales se presenta en la siguiente tabla:
Año
??
??
Valores de tendencia
?? = 9,464 + 0,995?? – 0,01??2
1960
1965
1970
1975
1980
1985
1990
1995
2000
2005
2010
-5
-4
-3
-2
-1
0
1
2
3
4
5
4,52
5,18
6,25
7,42
8,16
9,12
10,92
11,62
12,68
13,12
13,97
4,24
5,32
6,39
7,43
8,46
9,46
10,45
11,41
12,36
13,28
14,19
3) Para estimar la población de los años 2015 y 2020 se transforma estos años a X siguiendo la
secuencia de la tabla anterior, siendo X = 6 para el año 2015 y X= 7 para el 2020
Entonces para el 2015 se tiene:
Y = 9,464 + 0,995X – 0,01X2 =9,464 + 0,995(6) – 0,01(6)2 = 9,464 + 5,97-0,36 =15,074
Para el 2020 se tiene:
Y = 9,464 + 0,995X – 0,01X2 =9,464 + 0,995(7) – 0,01(7)2 = 9,464 + 6,965-0,49 =15,939

{
4) El diagrama de dispersión y la parábola de los mínimos cuadrados en GeoGebra:
REGRESIÓN EXPONENCIAL
Cuando la curva de regresión de y sobre x es exponencial, es decir para cualquier x considerada, la
media de la distribución está dada por la siguiente ecuación predictora:
?? = ?? · ?? ??
Tomando logaritmos en ambos miembros:
???????? = ???????? + ?? · ????????
Y se puede estimar ahora log Y y log ß, y de ahí obtener ?? y ??, aplicando los métodos de los mínimos
cuadrados.
Donde las constantes ?? y ?? quedan fijadas al resolver simultáneamente las ecuaciones:
S???????? = ???????? · ?? + ???????? · SX
SX · logY = loga · SX + logß · S??2
Ejemplo ilustrativo: Las cifras siguientes son datos sobre el porcentaje de llantas radiales producidas
por cierto fabricante que aún pueden usarse después de recorrer cierto número de millas:
Miles de Millas recorridas (X)
Porcentaje útil (Y)
1
99
2
95
5
85
15
55
25
30
30
24
35
20
40
15
1) Ajustar una curva exponencial aplicando el método de mínimos cuadrados.
2) Calcular la ecuación predictora.
3) Graficar la ecuación predictora.
4) Estimar qué porcentaje de las llantas radiales del fabricante durarán 50000 millas.

2
{
{
?{
Solución:
1) Se llena la siguiente tabla:
??
1
2
5
15
25
30
35
40
??
99
95
85
55
30
24
20
15
????????
1,996
1,978
1,929
1,740
1,477
1,380
1,301
1,176
??2
1
4
25
225
625
900
1225
1600
?? · ????????
1,996
3,955
9,647
26,105
36,928
41,406
45,536
47,044
S?? = 153
S???????? = 12,97759
S?? = 4605 S?? · ???????? = 212,61769
Remplazando valores en el sistema se obtiene:
S???????? = ???????? · ?? + ???????? · SX
SX · logY = loga · SX + logß · S??2
12,97759 = loga · 8 + logß · 153
212,61769 = loga · 153 + logß · 4605
8loga + 153logß = 12,97759
153loga + 4605logß = 212,61769
Al resolver el sistema se obtiene:
??????a = 2,027495747; l????ß = -0,02119180389
Remplazando valores se obtiene:
???????? = ???????? + ?? · ???????? ? ???????? = 2,027496 – 0,02119??
Aplicando el antilogaritmo se obtiene:
a = anti log 2,027495747 = 106,536; ß = anti log(-0,02119180389) = 0,952
2) Remplazando en la ecuación predictora se obtiene:
?? = ?? · ?? ?? ? ?? = 106,536 · 0,952??
3) Realizando el diagrama de dispersión y los cálculos de la ecuación predictora de GeoGebra
insertando AjusteBaseExp[ < Lista de Puntos> ] se obtiene:
4) La estimación del porcentaje de llantas radiales que durarán 50000 millas se obtiene remplazando en
la ecuación predictora el valor de X = 50
?? = 106,536 · 0,952?? ? ?? = 106,536 · 0,95250 = 9,106
Entonces el porcentaje sería de 9,106%

{
??
1
4
5
6
7
S?? = 28
{
REGRESIÓN POTENCIAL
La regresión potencial tiene por ecuación predictora:
?? = ?? · ????
Y la regresión recíproca es:
?? =
1
?? + ?? · ??
Para el primer caso los valores siguen una ley potencial. Si la ecuación predictora está dada por:
?? = ?? · ???? tomando logaritmos en ambos miembros, queda:
???????? = ???????? + ?? · ????????
Donde las constantes ?? y ?? quedan fijadas al resolver simultáneamente las ecuaciones:
S???????? = ???????? · ?? + ?? · SlogX
SlogX · logY = loga · SlogX + ß · S(????????)2
Para el segundo caso, si la ecuación predictora está dada por ?? =
1
??+??·??
misma expresión se puede escribir =
, o sea:
??
1
1 1
?? =
? = ?? + ?? · ??
?? + ?? · ?? ??
1
??+??·??
, entonces invirtiendo, la
Donde las constantes ?? y ?? quedan fijadas al resolver simultáneamente las ecuaciones:
1
S = ?? · ?? + ?? · SX
{
SX · = ?? · SX + ß · S??2
??
Ejemplos ilustrativo N° 1: Sea el siguiente conjunto de valores, las lecturas de un experimento donde
X es el volumen (variable independiente) e Y es la presión de una masa dada de gas (variable
resultante).
X 1 2 3 4
5
6
7
Y 7 30 90 170 290 450 650
1.1) Ajustar una curva exponencial aplicando el método de mínimos cuadrados.
1.2) Calcular la ecuación predictora.
1.3) Graficar la ecuación predictora.
1.4) Estimar la presión de la masa de gas de volumen 9.
Solución:
1.1) Para ajustar una curva exponencial aplicando el método de mínimos cuadrados:
??
1
2
3
??
7
30
90
170
290
450
650
????????
0,0000
0,3010
0,4771
0,6021
0,6990
0,7782
0,8451
????????
0,8451
1,4771
1,9542
2,2304
2,4624
2,6532
2,8129
???????? · ????????
0,0000
0,4447
0,9324
1,3429
1,7211
2,0646
2,3772
(????????)2
0,0000
0,0906
0,2276
0,3625
0,4886
0,6055
0,7142
S???????? = 3,7024 S???????? = 14,4354 S???????? · ???????? = 8,8829 S(????????)2 = 2,4890
Remplazando valores en el sistema de ecuaciones se obtiene:
S???????? = ???????? · ?? + ?? · SlogX
SlogX · logY = loga · SlogX + ß · S(????????)2

{
?{
14,4354 = ???????? · 7 + ?? · 3,7024
8,8829 = ???????? · 3,7024 + ?? · 2,4890
7???????? + 3,7024?? = 14,4354
3,7024???????? + 2,4890?? = 8,8829
Al resolver el sistema se obtiene: log a = 0,819; ß = 2,351
Remplazando valores en la ecuación predictora expresada en logaritmos se tiene:
???????? = ???????? + ?? · ???????? ? ???????? = 0,819 + 2,351 · ????????
1.2) Para calcular la ecuación predictora, primero se calcula el valor de a de la siguiente manera:
???????? = 0,819 ? ?? = ?????????????? 0,819 = 6,592
Remplazando en la ecuación predictora se obtiene:
?? = ?? · ???? ? ?? = 6,592 · ??2,351
1.3) Realizando el diagrama de dispersión y calculando la ecuación predictora en GeoGebra:
1.4) Para estimar la presión de la masa de gas de volumen 9 se reemplaza el valor X = 9 en la ecuación
predictora
?? = 6,592 · ??2,351 ? ?? = 6,592 · 92,351 = 1154,63
Ejemplo ilustrativo N° 2: Sea el siguiente conjunto de valores, las lecturas de un experimento donde
X es la variable independiente e Y la variable resultante.
X 1
2 3
4
5
6
7
Y 1,4 1 0,9 0,7 0,6 0,55 0,5
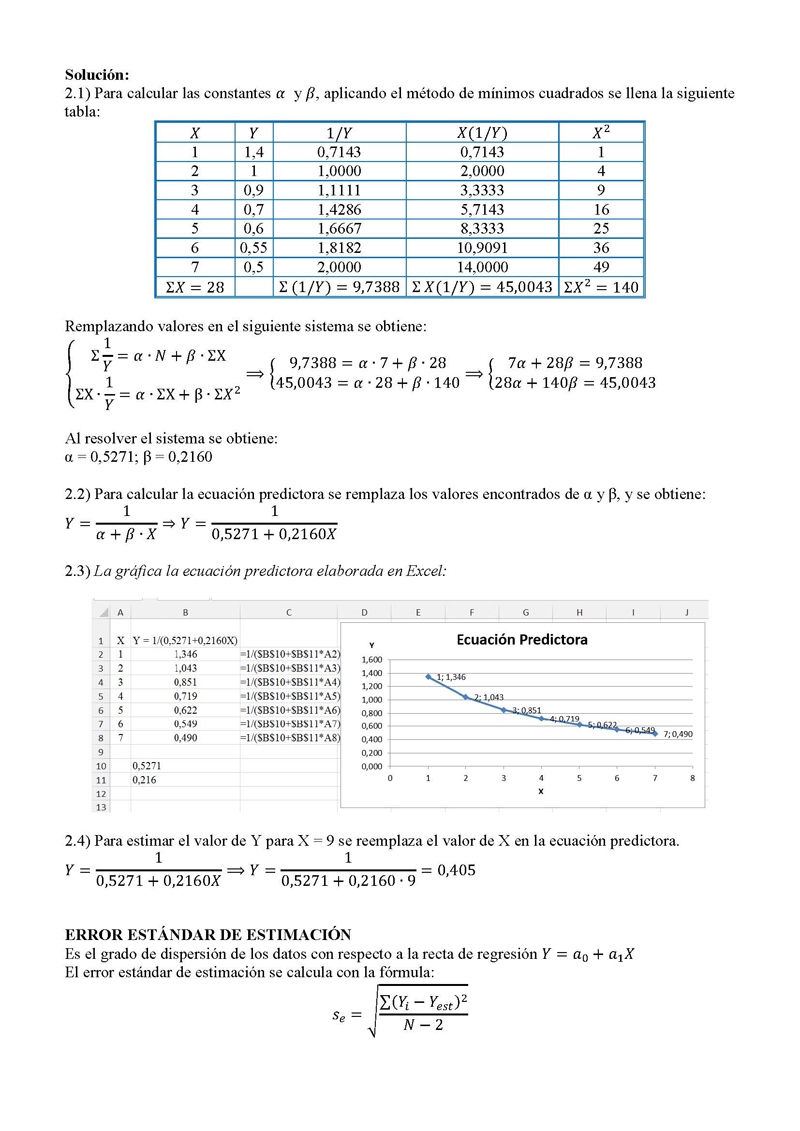
2.1) Calcular las constantes ?? y ??, aplicando el método de mínimos cuadrados.
2.2) Calcular la ecuación predictora.
2.3) Graficar la ecuación predictora.
2.4) Estimar el valor de Y para X = 9
2
{
Solución:
2.1) Para calcular las constantes ?? y ??, aplicando el método de mínimos cuadrados se llena la siguiente
tabla:
??
1
2
3
4
5
6
7
??
1,4
1
0,9
0,7
0,6
0,55
0,5
1/??
0,7143
1,0000
1,1111
1,4286
1,6667
1,8182
2,0000
??(1/??)
0,7143
2,0000
3,3333
5,7143
8,3333
10,9091
14,0000
??2
1
4
9
16
25
36
49
S?? = 28
S (1/??) = 9,7388 S ??(1/??) = 45,0043 S?? = 140
Remplazando valores en el siguiente sistema se obtiene:
1
S = ?? · ?? + ?? · SX
??
1
SX · = ?? · SX + ß · S??2
??
?{
9,7388 = ?? · 7 + ?? · 28
45,0043 = ?? · 28 + ?? · 140
?{
7?? + 28?? = 9,7388
28?? + 140?? = 45,0043
Al resolver el sistema se obtiene:
a = 0,5271; ß = 0,2160
2.2) Para calcular la ecuación predictora se remplaza los valores encontrados de a y ß, y se obtiene:
?? =
1
?? + ?? · ??
? ?? =
1
0,5271 + 0,2160??
2.3) La gráfica la ecuación predictora elaborada en Excel:
2.4) Para estimar el valor de Y para X = 9 se reemplaza el valor de X en la ecuación predictora.
?? =
1
0,5271 + 0,2160??
? ?? =
1
0,5271 + 0,2160 · 9
= 0,405
ERROR ESTÁNDAR DE ESTIMACIÓN
Es el grado de dispersión de los datos con respecto a la recta de regresión ?? = ??0 + ??1 ??
El error estándar de estimación se calcula con la fórmula:
???? = v
?(???? – ???????? )2
?? – 2

???? = v
¯
¯
???? = v
???? = v
8-2
= 4,556
Donde:
???? = cada valor de Y
???????? = valor estimado de Y a partir de la recta de regresión
N = número de datos
Otras ecuaciones para calcular el error estándar de estimación son:
? ??2 – ??0 ? ?? – ??1 ? ????
?? – 2
???? = v
? ?? 2 – ??1 ? ????
?? – 2
Donde:
??0 = ordenada en el origen (punto de intersección de la recta con el eje y)
??1 = pendiente de la recta (tangente del ángulo de inclinación de la recta)
?? = ?? – ??
?? = ?? – ??
Ejemplo ilustrativo: Calcular error estándar de estimación empleando las 3 fórmulas dadas, utilizando
los datos de la tabla del ejemplo para ajustar la recta de mínimos cuadrados para Y como variable
dependiente.
X 152 157 162 167 173 178 182 188
Y 56 61 67 72 70 72 83 92
Solución:
Para comenzar a resolver este ejemplo recordemos que ya se obtuvo los valores respectivos al resolver
el ejemplo para ajustar la recta de mínimos cuadrados, los cuales fueron:
S?? = 1359; S?? = 573; S???? = 98295; S??2 = 231967; S??2 = 41967; S???? = 956,625
S??2 = 1106,875; S??2 = 925,875; ??0 = -75,191; ??1 = 0,864; ?? = -75,191 + 0,864??
1) Para emplear la primera fórmula se llena la siguiente tabla:
??
152
157
162
167
173
178
182
188
??
56
61
67
72
70
72
83
92
???????? = 75,191 + 0,86??
-75,191+0,86(152)
-75,191+0,86(157)
-75,191+0,86(162)
-75,191+0,86(167)
-75,191+0,86(173)
-75,191+0,86(178)
-75,191+0,86(182)
-75,191+0,86(188)
????????
55,529
59,829
64,129
68,429
73,589
77,889
81,329
86,489
(?? – ???????? )2
0,222
1,371
8,243
12,752
12,881
34,680
2,792
30,371
S
Se remplaza valores en la primera fórmula se obtiene:
103,312
?(???? – ???????? )2
?? – 2
103,312
=v
8-2
= 3,842
2) Remplazando valores en la segunda fórmula se obtiene:
? ??2 – ??0 ? ?? – ??1 ? ????
?? – 2
41967 – (-75,191)(573) – 0,864(98295)
???? = v
41967 + 43084,443 – 84926,88
=v
6

???? = v
3) Remplazando valores en la tercera fórmula se obtiene:
? ??2 – ??1 ? ????
?? – 2
925,875 – 0,864(956,625)
=v
8-2
=v
99,351
6
= 4,069
Empleando exclusivamente Excel para calcular el error estándar de estimación se procede de la
siguiente manera:
Se inserta la función ERROR.TIPICO.XY. Se selecciona las celdas respectivas. Pulsar en Aceptar.
Interpretación: El valor de ???? = 4,064, significa que los puntos están dispersos a una distancia de
4,064 de la recta de regresión.
Fuente:
Suárez, Mario. & Tapia, Fausto. (2014). Interaprendizaje de Estadística Básica. Ibarra, Ecuador:
Universidad Técnica de Norte
Suárez, Mario. (2014). Probabilidades y Estadística empleando las TIC. Ibarra, Ecuador: Imprenta
GRAFICOLOR
Libros y artículos del Mgs. Mario Suárez sobre Aritmética, Álgebra, Geometría, Trigonometría, Lógica Matemática,
Probabilidades, Estadística Descriptiva, Estadística Inferencial, Cálculo Diferencial, Cálculo Integral, y Planificaciones
Didácticas se encuentran publicados en:
http://es.scribd.com/mariosuarezibujes
http://repositorio.utn.edu.ec/handle/123456789/760
http://www.docentesinnovadores.net/Usuarios/Ver/29591
