
1 Objetivos Definir el concepto de Funciones de red Definir la
función de red en términos de polos y ceros.
Elaborar diagramas de BODE (Magnitud y Fase), considerando los
siguientes factores: términos constantes, polos y ceros en
el origen y de orden "N", polos y ceros simples, polos y ceros
cuadráticos de redes eléctricas. 5.1
Introducción 5.2 Análisis de respuesta de
frecuencia variable. Funciones de la red. Polos y ceros. 5.3
Análisis de frecuencia compleja Respuesta utilizando el
diagrama de Bode: Términos constantes, Polo o ceros en el
origen de orden 'n' Polo o cero simple, Polos o ceros
cuadráticos Contenido

2 Una red que contiene un capacitor y una bobina opera de manera
diferente si se cambia la frecuencia. Esto se debe a que la
impedancia de ambos elementos del circuito dependen de la
frecuencia. Si la frecuencia de las fuentes de la red
varía en algún rango, podemos esperar que
también la red experimente variaciones en respuesta a esos
cambios de frecuencia. 5.1 Introducción Un ejemplo
concreto es un amplificador estereofónico. La señal
de entrada contiene ondas de sonido con frecuencias que van de
principio a fin; y, sin embargo, el amplificador debe ampliar
cada componente de frecuencia exactamente en la misma
proporción a fin de alcanzar una reproducción
perfecta del sonido Esto no es una tarea trivial, y cuando Usted
compra un muy buen amplificador, parte del precio refleja el
diseño necesario para lograr una amplificación
constante sobre la amplia gama de frecuencias.

3 Los dispositivos de comunicación modernos utilizan
dispositivos llamados filtros para separar las señales
eléctricas en base a su contenido en frecuencia. Por lo
tanto, es importante describir las relaciones que dependen de la
frecuencia, tanto la amplitud como la fase, entre la señal
senoidal de entrada y la señal senoidal de salida. Nuestro
estudio consistirá en examinar el funcionamiento de redes
eléctricas cuando son excitadas por fuentes de frecuenta
variable. Estos efectos son importantes en el análisis y
diseño de redes reales como filtros, sintonizadores y
amplificadores que tienen una extensa aplicación en
sistemas de comunicación y control. La respuesta en
frecuencia de un circuito es la relación dependiente de la
frecuencia, tanto en magnitud como en fase, entre una entrada
senoidal de estado estable y una señal de salida senoidal
de estado estable.

4 La impedancia de la Resistencia es: ZR = R = R|0o, donde la
magnitud y la fase son constantes e independientes de la
frecuencia. La gráfica de magnitud y fase de la impedancia
del Resistor en el dominio de la frecuencia se muestra en la
Figura 1. 5.2 Análisis de la respuesta de frecuencia
variable La impedancia de la Bobina es: ZL = j?L = ?L|90o, donde
la fase es constante a 90º pero la magnitud es directamente
proporcional a la frecuencia. La gráfica de magnitud y
fase de la impedancia de la Bobina en el dominio de la frecuencia
se muestra en la Figura 2.

5 La impedancia del Capacitor es: ZC = 1/j?C = (1/?C)|-90o, donde
la fase es constante a -90º pero la magnitud es inversamente
proporcional a la frecuencia. La gráfica de magnitud y
fase de la impedancia del Capacitor en el dominio de la
frecuencia se muestra en la Figura 3.

6 Ahora veamos el circuito RLC serie mostrado en la Figura 4,
donde la impedancia equivalente es:

7 La Figura 5 muestra la magnitud y fase de esta impedancia en
función de la frecuencia. Observe que a muy bajas
frecuencia, el capacitor aparece como un circuito abierto y, por
consiguiente la impedancia es muy grande en esta escala. A altas
frecuencias el capacitor tiene un efecto muy pequeño y la
impedancia es dominada por la bobina, cuya impedancia se sigue
elevando con la frecuencia.

8 A medida que los circuitos se hacen más complicados, las
ecuaciones se vuelven más molestas. En un intento por
simplificarlas, hacemos la sustitución s=j? (Esta
sustitución tiene un significado más importante).
Con esta sustitución, la expresión para la
impedancia Zeq se convierte en: Si revisamos los cuatros
circuitos vistos hasta aquí, encontramos que en cada caso
la impedancia es la razón de dos polinomios en s y es de
la forma general Esta ecuación es válida para
impedancias y también para todos los voltajes, las
corrientes, las admitancias y las ganancias en la red. La
única restricción es que los valores de todos los
elementos de circuito (resistencias, capacitores, bobinas y
fuentes dependientes) deben ser números reales.

9 Considere la red que se muestra en la Figura 6. Se desea
determinar la variación del voltaje de salida como
función de la frecuencia en la escala de 0 a 1KHz. Ejemplo
Usando el divisor de voltaje, la salida puede expresarse como
Solución

10 Utilizando los valores de los elementos, la ecuación se
convierte en: En este punto podemos sustituir simplemente los
diferentes valores de la frecuencia en la escala de
interés en la ecuación, y determinar la magnitud y
fase del voltaje de salida. Usando un gran número de esos
puntos podemos hacer gráficas de la magnitud y fase del
voltaje de salida como función de la frecuencia. Este
efectivo pero tedioso método puede simplificarse bastante
si se aplica un software (Pspice, Matlab, etc). Las
gráficas que resultan de la magnitud y la fase se muestran
en la Figura 7.

11 La función de red es designada generalmente como H(s),
y define la razón de respuesta a la entrada. Como la
función describe una reacción debida a una
excitación en algún otro punto del circuito, las
funciones de la red de estación también se llaman
funciones de transferencia. Además, las funciones de
transferencias no están limitadas a razones de voltaje. Lo
mismo que en redes eléctricas, las entradas o salidas
pueden ser voltajes o corrientes hay cuatro posibles de la red,
como se enlista en la siguiente tabla. Funciones de la red

12 Ejemplo También hay funciones de puntos de entrada, que
son impedancias o admitancias definidas en un solo par de
terminales. Por ejemplo, la impedancia de entrada de una red es
una función de entrada. Para el circuito mostrado en la
Figura 8, determine la Transadmitancia [I2(s)/V1(s)] y la
ganancia de voltaje.

13 Solución Haciendo LKV a la malla 1 se obtiene:
Resolviendo las ecuaciones para I2(s) se obtiene: (R1+sL)I1(s)
– sLI2(s) = V1(s) Haciendo LKV a la malla 2 se obtiene:
-sLI1(s) + (R2+sL+1/sC)I2(s) = 0 V2(s) = I2(s)R2 Por lo tanto, la
Transadmitancia es:

14 Y la ganancia de voltaje es: Polos y Ceros Como hemos indicado
anteriormente, la función de red puede expresarse como la
razón de los dos polinomios en s. Además notamos
que como los valores de nuestros elementos de circuitos, o
fuentes controladas, son números reales, los coeficientes
de los dos polinomios serán reales. Por lo tanto,
expresamos una función de red en la forma:

15 donde N(s) es el polinomio del numerador de orden m y D(s) es
el polinomio del denominador de orden n. La ecuación
anterior también puede escribirse en la forma siguiente:
Donde Ko es una constante, z1, ?, zm son las raíces de
N(s), y p1, ?, pn son las raíces de D(s). Observe que si
s=z1, o z2, ?, zm, entonces H(s) se hace cero y de aquí
z1, ?, zm se llaman ceros de la función de transferencia.
De manera similar, si s=p1, o p2, ?, pn, entonces H(s) se hace
infinito y, por consiguiente p1, ?, pm se llaman ceros polos de
la función de transferencia. Los ceros o polos realmente
son complejos. Sin embargo, si ellos son complejos deben
presentarse en pares conjugados, ya que los coeficientes de los
polinomios son reales

16 La representación de la función de la red
especificada en términos de polos y ceros, es
extremadamente importante y en general se emplea para representar
cualquier sistema lineal invariante en el tiempo. La importancia
de esta forma se deriva del hecho de que las propiedades
dinámicas de un sistema pueden recogerse de un examen de
los polos del sistema. 5.3 Análisis de frecuencia senoidal
Aunque hay casos específicos en los que una red opera a
sólo una frecuencia (por ejemplo, la red del sistema de
potencia), en general estamos interesados en el comportamiento de
una red como función de la frecuencia. En análisis
senoidal de estado estable, la función de la red puede
expresarse como: donde M(?)=|H(j?)| y ?(?) es la fase. Una
gráfica de esas dos funciones, que se llaman
comúnmente magnitud y característica de fase,
despliega la forma en que la respuesta varía con la
frecuencia de entrada ?.

17 Si las características de la red son trazadas en una
escala semilogarítmica, es decir, una escala lineal para
la ordenada y una escala logarítmica para la abscisa, se
conocen como gráficas de Bode (llamadas así en
recuerdo de Hendrik W. Bode). Respuesta de frecuencia usando una
gráfica de Bode Esta gráfica es una herramienta
poderosa en el análisis y diseño de sistemas
dependientes de la frecuencia y de las redes, como filtros,
sintonizadores y amplificadores. Al usar la gráfica,
hacemos gráficas de 20log10M(?) contra log10(?) en vez de
M(?) contra (?). La ventaja de esta técnica es que
más que trazar las características punto por punto,
podemos emplear aproximaciones en línea recta para obtener
la característica de manera muy eficiente. La ordenada
para la gráfica de la magnitud es el decibel (dB). Esta
unidad fue empleada originalmente para medir la razón de
potencias, es decir: número en dB =10log10(P2/P1)

18 Si las potencia son absorbidas por dos resistencias iguales,
entonces El término “dB” ha llegado a ser tan
popular que ahora se usa para razones de voltaje y corriente,
como se ilustra en la ecuación anterior, haciendo caso
omiso de la impedancia empleada en cada caso. En el caso senoidal
en estado estable, H(j?) puede escribirse en general como:

19 Recuerde que s=j? y ?=1/?, entonces la ecuación
anterior se puede escribir como: Observe que ambas ecuaciones
contienen los siguientes factores típicos: 1. Un factor
Ko>0 independiente de la frecuencia. 2. Polos o ceros en el
origen de la forma j?, es decir, (j?)+N para ceros y (j?)-N para
polos. 3. Polos o ceros de la forma (1+j??). 4. Polos o ceros
cuadráticos de la forma 1 + 2?(j??) + (j??)2.

20 Tomando el logaritmo de la magnitud de la función H(j?)
se obtiene: 20log10|H(j?)| = 20log10Ko ? 20Nlog10|j?| +
20log10|1+j??1| Observe que hemos usado el hecho de que el
logaritmo del producto de dos o más términos es
igual a la suma de los términos individuales, el logaritmo
del cociente de dos términos es igual a la diferencia de
los logaritmos individuales, y el hecho de que log10An = nlog10A.
El ángulo de fase para H(j?) es: +
20log10|1+2?3(j??3)+(j??3)2| + ? – 20log10|1+j??a| –
20log10|1+2?b(j??b)+(j??b)2| – ? |H(j?) = 0 ? N(90º)
+tan-1??1

21 Examinemos algunos de los términos individuales e
ilustremos una manera eficiente de graficarlos en un diagrama de
Bode. El diagrama de magnitud es una línea horizontal
puesta a: 0 dB si |Ko| = 1 bajo de 0 dB si |Ko| < 1 arriba del
0 dB si |Ko| > 1 Funciones con frecuencia invariante (Termino
constante) H(s) = Ko, entonces |H(s)|dB = 20log10Ko

22 El diagrama de fase es una línea horizontal puesta a:
0o si Ko es positiva -180º si Ko es negativa

23 El diagrama de magnitud es una línea con pendiente de
+20 dB/década sobre todo el rango de frecuencias, para el
caso de un cero. Si ?/?o = 1, la curva pasa por 0 dB. Funciones
con raíces en el origen (polos o ceros en el origen) H(s)
= (s/?o)?1, el signo + si la raíz es un cero y el signo
– si la raíz es un polo |H(s)|dB =
?20log10(?/?o)
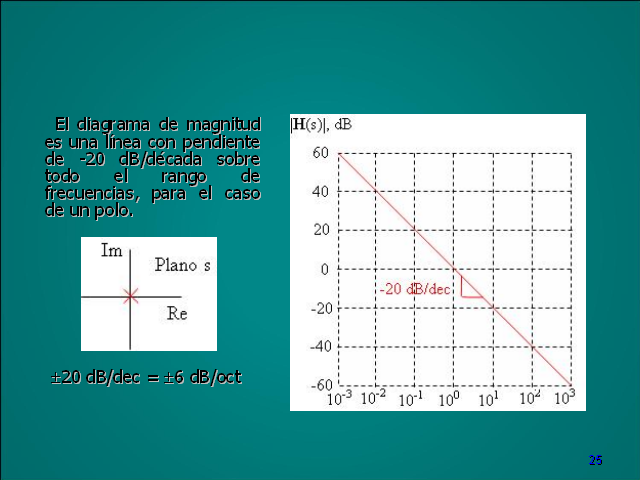
24 El diagrama de magnitud es una línea con pendiente de
-20 dB/década sobre todo el rango de frecuencias, para el
caso de un polo. ?20 dB/dec = ?6 dB/oct

25 El diagrama de fase es una línea horizontal a +90º
sobre todo el rango de frecuencias, para el caso de un
cero.

26 El diagrama de fase es una línea horizontal a -90º
sobre todo el rango de frecuencias, para el caso de un
polo.
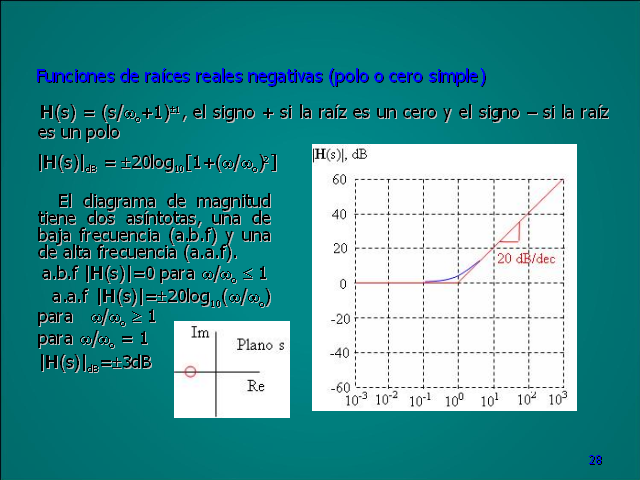
27 El diagrama de magnitud tiene dos asíntotas, una de
baja frecuencia (a.b.f) y una de alta frecuencia (a.a.f). a.b.f
|H(s)|=0 para ?/?o ? 1 a.a.f |H(s)|=?20log10(?/?o) para ?/?o ? 1
Funciones de raíces reales negativas (polo o cero simple)
H(s) = (s/?o+1)?1, el signo + si la raíz es un cero y el
signo – si la raíz es un polo |H(s)|dB =
?20log10[1+(?/?o)2] para ?/?o = 1 |H(s)|dB=?3dB

28 El diagrama de magnitud tiene dos asíntotas, una de
baja frecuencia (a.b.f) y una de alta frecuencia (a.a.f). a.b.f
|H(s)|=0 para ?/?o ? 1 a.a.f |H(s)|=?20log10(?/?o) para ?/?o ? 1
para ?/?o = 1 |H(s)|dB=?3dB

29 El diagrama de fase tiene dos asíntotas, una de baja
frecuencia (a.b.f) y una de alta frecuencia (a.a.f). a.b.f
?H(s)=0o para ?/?o ? 0.1 a.a.f ?H(s)=?90º para ?/?o ? 10.
Para 0.1 ? ?/?o ? 10 existen pendientes de ?45º para ?/?o =
1 ?H(s) =?45º para ?/?o = 0.1 y ?/?o = 10 la fase tiene
desviaciones de cerca 6º.

30 El diagrama de fase tiene dos asíntotas, una de baja
frecuencia (a.b.f) y una de alta frecuencia (a.a.f). a.b.f
?H(s)=0o para ?/?o ? 0.1 a.a.f ?H(s)=?90º para ?/?o ? 10.
Para 0.1 ? ?/?o ? 10 existen pendientes de ?45º para ?/?o =
1 ?H(s) =?45º para ?/?o = 0.1 y ?/?o = 10 la fase tiene
desviaciones de cerca 6º.

31 El diagrama de magnitud tiene dos asíntotas, una de
baja frecuencia (a.b.f) y una de alta frecuencia (a.a.f). a.b.f
|H(s)|=0 para ?/?o ? 1 a.a.f |H(s)|=?40log10(?/?o) para ?/?o ? 1
Funciones con pares de raíces complejas (polos o ceros
cuadráticos) H(s) = [(s/?o)2+2?(s/?o)+1]?1, el signo + si
la raíz es un cero y el signo – si la raíz es
un polo |H(s)|dB = ?10log10{[1+(?/?o)2]2+[2?(?/?o)]2} H(j?) =
[1-(?/?o)2+2?j(?/?o)]?1

32

33

34 El diagrama de fase tiene dos asíntotas, una de baja
frecuencia (a.b.f) y una de alta frecuencia (a.a.f). a.b.f
?H(s)=0o para ?/?o ? 0.1 a.a.f ?H(s)=?180º para ?/?o ? 10.
Para 0.1 ? ?/?o ? 10 existen pendientes de ?90º

35

36 Las aproximaciones en línea rectas (asíntotas),
para este caso son satisfactorias para ? cerca 1/?2, pero para
pequeños valores de ? debemos aplicar correcciones para
reflejar la presencia de un pico. Estas correcciones son hechas
en los siguientes puntos significantes. 1) a la frecuencia de
corte, es decir, ?/?o = 1, entonces |H(s)|dB = ?20log102? 2) a la
frecuencia donde se da el pico, ?/?o = ?(1-?2), entonces |H(s)|dB
= ?10log10[4?2(1-?2)] 3) una octava debajo de la frecuencia de
corte, es decir ?/?o = 1/2, entonces |H(s)|dB =
?10log10(?2+0.752) 4) a la frecuencia a la cual la curva de
magnitud cruza el eje de 0 dB, ?/?o = ?[2(1-2?2)] 5) a la fase,
una octava debajo de la frecuencia de corte, es decir, ?/?o =
1/2, entonces ?H(s) = ?tan-1(?/0.75)

37 6) a la fase, una octava arriba de la frecuencia de corte, es
decir, ?/?o = 2, entonces ?H(s) = ?[180-tan-1(?/0.75)] En las
siguientes Figuras se muestran los puntos de las correcciones que
se deben hacer

38 Como estamos usando una hoja milimetrada, es necesario
introducir la definición de intervalo de década o
llamado también ciclo. Dado un valor de frecuencia
específica dentro del ciclo 10n ? ? ? 10n+1 rad/s, su
localización “l” dentro del ciclo es:
Múltiples raíces Si una raíz o una pareja de
raíces complejas tienen multiplicidad r, entonces el
término correspondiente tiene la forma Hr. Así
tenemos: |Hr(j?)|dB = r*|H(j?)|dB ?Hr(j?) = r*?H(j?)

39 Localizar 320 rad/s, y 2000 rad/s Ejemplo Solución 102
rad/s ? 320 rad/s ? 103 rad/s, entonces: 103 rad/s ? 2000 rad/s ?
104 rad/s, entonces:
