Las leyes de Kepler a partir de la conservación de momento angular
Las leyes de Kepler a partir de la conservación de momento angular
La torca  producida por una fuerza central
producida por una fuerza central  está dada por la expresión:
está dada por la expresión:
 (1)
(1)
En donde:  es un vector de posición
es un vector de posición
Dado que geométricamente se satisface:  II
II 
1a Ley de Kepler. "Los planetas se mueven siguiendo trayectorias cerradas (elípticas) que están contenidas en un plano ( con el sol en uno de sus focos)"
Considerando la siguiente figura:
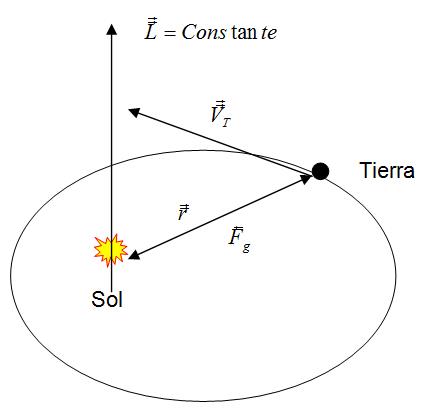
En donde:
 Corresponde a la fuerza gravitacional entre el sol y la tierra.
Corresponde a la fuerza gravitacional entre el sol y la tierra.
 Corresponde a la distancia entre el centro del sol y la tierra.
Corresponde a la distancia entre el centro del sol y la tierra.
 Corresponde a la velocidad tangencial de la tierra en su trayectoria elíptica.
Corresponde a la velocidad tangencial de la tierra en su trayectoria elíptica.
Dado que  es radial a la trayectoria de la Tierra alrededor del sol, entonces de la expresión (1) se establece:
es radial a la trayectoria de la Tierra alrededor del sol, entonces de la expresión (1) se establece:
Si entonces
entonces 
(Dado que se satisface:  )
)
Por lo tanto la trayectoria cerrada que describe la tierra alrededor del sol corresponde a un plano.
2a Ley de Kepler. "Durante intervalos iguales de tiempo, una línea que une al sol al planeta (por ejemplo la Tierra) barre áreas iguales en cualquier parte de su trayectoria"
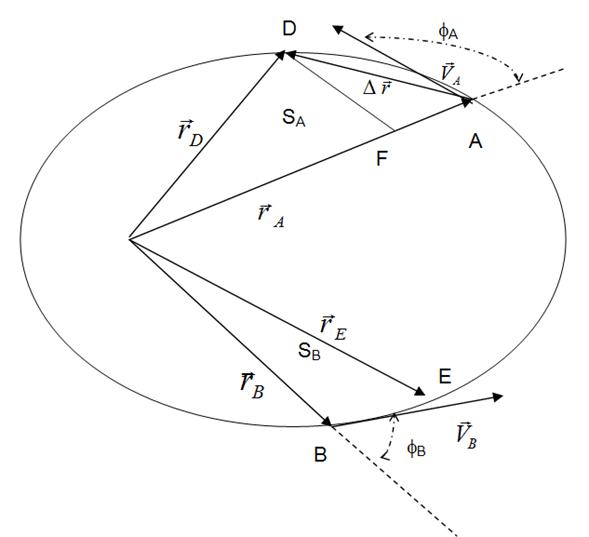
La magnitud del momento angular en el punto A, esta dado por:

La magnitud del momento angular en el punto B, esta dado por:

Dado que las Orbitas son estables entonces:

Es decir:
 (2)
(2)
Para la superficie SA se obtiene:

El área del triangulo ADC es equivalente a SA que esta dada por:

En donde:  sustituyendo este resultado la relación anterior de SA, resulta:
sustituyendo este resultado la relación anterior de SA, resulta:
 (3)
(3)
Ahora:
D F = D A sen ( (4)
Dado que: ( + (A = 180o, es decir: ( = 180o – (A, entonces se satisface:
sen ( = sen (A
Sustituyendo la expresión anterior en la relación (4), resulta:
D F = D A sen (A
Sustituyendo la relación anterior en la ecuación (4), se obtiene:
 (5)
(5)
Considerando que: 
Sustituyendo la relación anterior en la ecuación (5), resulta:
 (6)
(6)
Dado que:

Sustituyendo la relación anterior en la expresión (6), resulta:
 (7)
(7)
En forma análoga si el cuerpo se encuentra en el punto B y se mueve en dirección al punto E, resulta:
 (8)
(8)
De las condiciones expresadas en las ecuaciones (2), (7) y (8) se infiere:

Por lo tanto:
SA = SB
3a Ley de Kepler. " El cuadrado del periodo de un planeta es proporcional al cubo de su distancia media al sol"
Para una velocidad angular constante (, la aceleración centrípeta ac a lo largo de su trayectoria cerrada, esta dada por:
 (9)
(9)
Dado que:

En donde:
T: corresponde al periodo.
Sustituyendo la relación anterior en la ecuación (9), se obtiene:
 (10)
(10)
Por consideraciones de estabilidad dinámica se estable:
 (11)
(11)
En donde:
Fg: corresponde a la fuerza gravitacional (central) que actúa entre el sol y el planeta.
Fc: corresponde a la fuerza centrípeta (central) ejercida por la trayectoria del planeta.
Dado que:
 (12)
(12)
En donde:
mT: corresponde a la masa terrestre.
MS: corresponde a la masa del sol.
G: corresponde a la constante de gravitación universal.
R: corresponde a la distancia del sol y la tierra.
Ahora:
 (13)
(13)
Sustituyendo (12) y (13) en (11), resulta:

Es decir:

Por lo tanto:

En donde, ( es una constante de proporcionalidad.
BIBLIOGRAFÍA.
-Alonso M y Finn E Física Vol. I Mecánica Edit. Addison- Wesley Iberoamericana (1970)
– McGill D. y King W Mecánica para ingeniería y sus aplicaciones II Dinámica Edit Grupo editorial Iberoamericana (19991)
-Resnick R., Holliday D., Física vol. 1, CECSA, 1993
