Compensación automática de fuerzas dinámicas en un rotor tipo Stodola-Green
Un análisis de un sistema de
autobalanceo es presentado en este artículo, el cual
utiliza cuerpos (bolas) balanceadores que se mueven libremente al
girar junto con el rotor por balancear. Utilizando las ecuaciones de
Lagrange´s, nosotros derivamos las ecuaciones no lineales
de movimiento
para un sistema autónomo con respecto a un sistema de
coordenadas polar. De las ecuaciones de movimiento para el
sistema autónomo, las posiciones de equilibrio y
las ecuaciones lineales del variacional son obtenidas por el
método de
perturbación. A causa de la resistencia para
el movimiento, la excentricidad, a una velocidad
excesiva hace a que los cuerpos balanceadores sean movidos y la
influencia de las vibraciones externas hace imposible lograr un
balanceo completo. Basado en las ecuaciones del variacional, la
estabilidad dinámica del sistema en la cercanía
de las posiciones de equilibrio se investiga. Los resultados del
análisis de estabilidad proporcionan los requerimientos de
diseño
para el sistema de atobalanceo.
1.- Introducción.
El desbalance es la distribución irregular de las masas de un
cuerpo respecto al centro geométrico de rotación,
dando como resultado la descompensación de masas que al
girar con cierta aceleración originan fuerzas excitadoras
radiales que causan desgaste, vibración, componentes
doblados o rotos y componentes excéntricos. Si se aplica
la técnica de balanceo automático a la maquinaria
rotatoria, se pueden eliminar problemas de
vibración por desbalance, dando como resultado mayor
disponibilidad y confiabilidad en la maquinaria rotatoria,
así como una mayor durabilidad de esta.
La rotación de cuerpos o rotores en desbalance
producen vibración y provocan cargas dinámicas
adicionales. Las altas velocidades de los equipos rotatorios
actuales hacen de este problema una necesidad rigurosa en
materia de
balance de las partes en movimiento. Sin embargo en un sistema
donde la distribución de las masas varía, durante
la operación o cada vez que tiene que ser arrancada
nuevamente por algún paro
técnico, el método convencional de balance de
rotores se vuelve impráctico.
Es aquí donde los métodos de
autobalance se pueden practicar y tratar de eliminar los tiempos
muertos de estos equipos por paros necesarios debido al
desbalance. Estos métodos de autobalance se basan en
mecanismos ya sea líquidos o cuerpos (péndulos,
bolas, etc.) que se posicionan en sentido opuesto a la fuerza que
provoca el desbalance. En el caso de un líquido, el grado
de balance que se puede lograr es del 50% del desbalance original
e inicial. Mientras que al utilizar péndulos o bolas es
teóricamente posible optimizar el balanceo al
100%.
En los mismos sistemas de
balanceo, la investigación básica se
comenzó por Thearle [2, 3], Alexander [4] y Cade [5]. El
análisis dinámico de las ecuaciones
diferenciales para los mismos sistemas de balanceo puede
encontrarse en las referencias [7-9]. Las ecuaciones obtenidas
son para los sistemas no autónomos, estas ecuaciones
tienen las limitaciones en el análisis de estabilidad.
Chung y Ro [9] estudiaron la estabilidad y la conducta
dinámica de un ABB para el rotor Jeffcott. Ellos derivaron
las ecuaciones de movimiento para un sistema autónomo
usando las coordenadas polares en lugar de las coordenadas
rectangulares. Hwang y Chung [10] aplicaron este acercamiento al
análisis de un ABB con carreras dobles. En este estudio,
los autores consiguieron un análisis similar para un eje
flexible con dos sistemas de balanceo. Describiendo el centro
geométrico del rotor con las coordenadas polares, se
derivan las ecuaciones no lineales de movimiento para un sistema
autónomo de la ecuación de Lagrange. Después
de una posición de equilibrio balanceado y linealizando
las ecuaciones en la cercanía de la posición de
equilibrio son obtenidas por el método de
perturbación.
Por un largo tiempo el
balanceo automático en un plano ha sido un fenómeno
bien conocido (según Blekhman 2000, sperling et al 1998).

Este método fue propuesto por Thearle para el
balanceo en un plano, desarrollando la metodología y verificando la eficiencia del
mismo. Mas adelante R. Sokolowska investigó la posibilidad
de compensar las fuerzas dinámicas por el objeto rotante y
comprobó que sólo una parte del desbalance
podría ser compensado por elementos libres.
Si el rotor tiene desbalance estático y
desbalance dinámico entonces existen fuerzas
centrífugas y momentos que giran con el rotor, donde estas
fuerzas actúan a lo largo de todo el sistema del rotor, en
un plano transversal; para esto es necesario introducir o crear
dos fuerzas, en planos previamente analizados, similares a las
fuerzas originadas por el desbalance pero en sentido opuesto,
tratando de llevar la vibración originada inicialmente a
cero. Esto se puede lograr con elementos rodantes en discos con
una arquitectura de
tal manera que las bolas o esferas busquen una posición a
180º de las fuerzas inerciales de origen.
Finalmente la aportación de la
investigación será la de realizar el
análisis dinámico para un rotor tipo Stodola-Green
aplicando una metodología similar a la que utilizaron los
investigadores mencionados anteriormente, en la cual
también se tendrá la tarea de realizar una simulación
computarizada para el sistema de ecuaciones, en la cual se
podrá observar el comportamiento
del sistema de balanceo.
Cabe destacar que esta teoría
será aplicable en casos como el de una lavadora; en donde
en la etapa de secado, la ropa no se distribuye uniformemente al
estar girando la tina. Lo cual esta mala distribución de
la ropa ocasiona que los soportes y los rodamientos tengan un
desgaste excesivo provocando que tengan una duración mas
corta. Este sistema automáticamente compensará esta
vibración y optimizará el comportamiento de los
elementos en cuestión.
Así como este ejemplo existen muchos otros, de
mayor o igual importancia, ya que el desbalanceo en maquinaria
rotatoria provoca una menor durabilidad de esta, además de
que de igual manera se pone en riesgo a las
personas que operan estos equipos. Algunos otros equipos que
podríamos mencionar en los cuales se pudiese implementar
un sistema de balanceo automático son: unidades de
CD-ROM,
maquinaria rotodinámica como son (turbinas, motores, etc.).
Así pues, el propósito fundamental de esta
investigación es la de eliminar el desbalance en la
maquinaria rotatoria por medio del balanceo
automático.

Figura 1.- Sistema de autobalanceo en
un rotor tipo Stodola-Green.
El rotor tipo Stodola-Green con un sistema de
autobalanceo es mostrado en la figura 1, en la cual la flecha del
rotor esta apoyado en uno de sus extremos por el mismo sistema de
autobalanceo. En este análisis es supuesto que la masa de
la flecha es despreciable comparado con la masa del rotor. El
sistema de coordenadas XYZ es un marco de referencia inercial con
un espacio-fijo y los puntos C y G son el centro de masa y
centroide del rotor respectivamente. El punto O puede ser
considerado como la proyección de centroide C hacía
el eje O`Z. El balanceador de bolas consiste de un rotor circular
con una ranura que contiene las bolas y un fluido humedecedor.
Las bolas se mueven libremente en la ranura y el rotor con
una velocidad angular ω. Es supuesto que la
deflexiσn de la flecha es pequeρa pero
puede asumirse que el centroide C se mueve en el plano
XY.
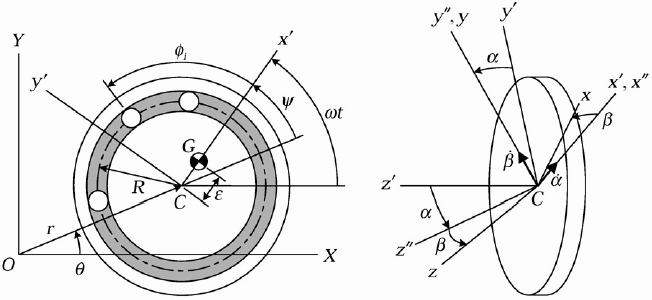
Figura 2.- Representación
esquemática del sistema de autobalanceo.
Como es mostrado en la Figura 2, el centroide C puede
definirse por las coordenadas polares r y
El centro de masa puede definirse por la excentricidad
y el ángulo t, para la
posición dada del centroide y la posición angular
de la bola Bi es dado por el radio de paso R y
el ángulo i.
Para describir las rotaciones del cuerpo rígido
del rotor en el eje X y Y, se usan los ángulos de Euler,
para dar orientación al rotor-fijo en el sistema de
coordenadas relativo xyz y para el espacio-fijo el sistema de
coordenadas XYZ. En este caso, los ángulos de Euler de
t, y son usados como se muestra en la
Figura 2. Una rotación a través del ángulo
t sobre el eje Z resulta en el primer sistema.
Semejantemente la rotación sobre el eje x´
y una rotación sobre el eje y´´
resulta el segundo sistema y el sistema de coordenadas xyz
respectivamente. En forma matricial:
![]() (1)
(1)
y las matrices de
rotación:
 (2)
(2)
![]() (3)
(3)
En la cual todos los componentes son vectores
unitarios alo largo de las direcciones asociadas
respectivamente.
En el primer paso es considerado la energía
cinética del rotor con el sistema de autobalanceo. El
vector de posición del centro de masa G puede ser
expresada usando la matriz de
rotación:
![]() (4)
(4)
En donde
![]() (5)
(5)
Usando una coordenada generalizada común
definida por
![]() (6)
(6)
Después del producto
matricial, el vector de posición del centro de masa,
rG es:
 (7)
(7)
Y el vector de posición de la bola:
 (8)
(8)
En este estudio nosotros estamos suponiendo que estamos
utilizando 2 bolas, en la cual la energía cinética
es dada por:
![]() (9)
(9)
Donde J es la matriz de inercia y es el vector
de la velocidad angular del rotor:
 (10)
(10)
![]() (11)
(11)
En el cual J es el momento de inercia de la masa sobre
el eje x,y,z. Despreciando la gravedad, el par torsional y la
deflexión longitudinal de la flecha, la energía
potencial o la emergía de tensión, forman los
resultados de la curva de deflexión de la flecha. Como se
muestra en la Figura 1. La flecha puede ser considerada como una
viga en cantiliver, en la cual es fijo en Z=0 y libre en Z=L. La
deflexión en la direcciones X y Y en Z=L, Dx y Dy, son
dadas por:
![]() (12)
(12)
Para los ángulos de rotación y
, los ángulos de rotación sobre los ejes X
y Y son:
![]() (13)
(13)
La deflexión y pendiente en Z=L en el plano ZX
son DX y Y, mientras que en el
plano ZY son DY y -X,
las deflexiones en las curvas de la flecha en los planos ZX y ZY,
δx y δy, pueden ser expresados como:
 (14)
(14)
En este caso, la energía de tensión V
esperado para la flecha deformada es:
 (15)
(15)
En donde E es el modulo de Young’s y I es el
momento de inercia del área de la sección de la
flecha.
En otras palabras, la función de
disipación de Rayleigh’s F puede ser representada
por:
![]() (16)
(16)
En donde ct y cr es
respectivamente el coeficiente de humedecimiento equivalente para
la traslación y rotación y D es el coeficiente de
viscosidad de
rozamiento de las bolas en el fluido humedecedor.
Las ecuaciones de movimiento son derivadas a
partir de la ecuación de Lagrange’s:
![]() (17)
(17)
En esta formula qk son las coordenadas
generalizadas. Para el sistema dado, las coordenadas
generalizadas son r,
y
por lo
tanto, el comportamiento dinámico del sistema de
autobalanceo es gobernado por 2+4 ecuaciones independientes de
movimiento. Bajo la suposición de que r,
son pequeños y sus
productos
también, las ecuaciones de movimiento son simplificadas y
linealizadas por el método de
perturbación:
![]() (18)
(18)
En este caso cada ecuación anterior tiene dos
componentes; las coordenadas para las posiciones de equilibrio y
sus pequeñas perturbaciones. Se considera que ![]() =0 en la posición
=0 en la posición
de equilibrio. Y las ecuaciones linealizadas de moviendo
son:
 (19)
(19)
 (20)
(20)
 (21)
(21)
 (22)
(22)
 (23)
(23)
Es supuesto en las 4 ecuaciones anteriores
que:
![]() (24)
(24)
Los momentos de inercia de la masa,
JX=JY y JZ son dadas
por:
![]() (25)
(25)
La posición del equilibrio
balanceado puede ser representada por:
 (26)
(26)
Las pequeñas perturbaciones de las coordenadas
generalizadas de la posición balanceada pueden ser
escritas como:
 (27)
(27)
y es un eigenvalor. Sustituyendo las ecuaciones
(26) y (27) en las ecuaciones (19-22), usando la ecuación
de identidad de
Pitágoras y la condición que dan las ecuaciones
(27), se tienen soluciones no
triviales que pueden ser expresadas como una ecuación
característica dada como:
![]() (28)
(28)
en donde los coeficientes
ck(k=0,1,….12) son funciones de
, M, m, R, L, , E, I, D, ct y
cr. Las expresiones explicitas de ck son
omitidas de este articulo. El criterio de Routh-Hurwitz mantiene
una condición suficiente para las partes reales de todas
las raíces para ser negativas. Los parámetros de la
geometría siguiente son considerados
como:
![]() (29)
(29)
Y o es la referencia de la
frecuencia; ty r
son factores de humedecimiento adimensionales para la
translación y rotación. En este articulo se estudia
la estabilidad del balanceador por las variaciones de los
parámetros de los sistemas no adimensionales como es
/o contra /R. Estos son
algunos parámetros para ser considerados: L/R=2, y m/M =
/R = D/mR2o =
t = r = 0.01.
Figura 3.- Posible posición de
equilibrio par alas variaciones de velocidad de
rotación.
Para ver el
gráfico seleccione la opción "Descargar" del
menú superior
Figura 4.- Representación
esquemática de 2 posiciones del rotor a) Posición
de equilibrio,
b) posición de
desequilibrio.
Los cuerpos balanceadores (bolas) del sistema de
autobalanceo no asumen las posiciones que aseguren el
balanceamiento completo del rotor. Las posiciones eficaces de un
cuerpo balanceador difieren por la posición de equilibrio
. Otras razones que
también pueden aparecer son la fricción de los
cuerpos balanceadores contra las caras que están
dispuestas dentro de ellos, irregularidades de forma o la
distribución del peso asimétrico axial de los
cuerpos balanceadores. Los errores de posición son
relativamente grandes y el mas grande de ellos es el alto
coeficiente de resistencia al movimiento rotativo y es la
razón mas alta de /o (cuando es
mayor que 1) Para reducir estos errores seria necesario cambiar
el método de guiado de los cuerpos balanceadores. Por
ejemplo aire amortiguado,
cuerpos suspendidos por fuerzas magnéticas o
electrostáticas.
Para obtener el balanceo, debe ser mayor que la
primera frecuencia natural, el fluido humedecedor D y la
disipación por translación ct son
necesarios para obtener el balanceo, pero la disipación
por rotación cr no lo es. La estabilidad del
sistema se ha analizado con las ecuaciones lineales del
variacional y el criterio de Routh-Hurwitz.
1.- J. N. MacDuff and J. R. Curreri, Vibration
Control, McGraw-Hill, New York (1958).
2.- E. L. Thearle 1950 Machine Design 22,
119-124. Automatic dynamic balancers (Part 1.
leblanc).
3.- E. L. Thearle 1950 Machine Design 22,
103-106. Automatic dynamic balancers (Part 2. ring, pendulum,
ball balancers).
4.- J. D. Alexander 1964 Proceedings of
2nd Southeastern Conference vol. 2, 415-426. An
automatic dynamic balancer.
5.- J. W. Cade 1965 Design News, 234-239.
Self-compensating balancing in rotating mechanisms.
7.- Majewski Tadeusz 1988, Mechanism and Machine
Theory, Position Error Occurrence in Self Balancers Used in
Rigid Rotors of Rotating Machinery, Vol. 23, No. 1 pp71-78,
1988.
8.- C. Rajalingham and S. Rakheja 1998 Journal of
Sound and Vibration 217, 453-466. Whirl suppression in
hand-held power tool rotors using guided rolling
balancers.
9.- J. Chung and D. S. Ro 1999 Journal of Sound and
Vibration 228, 1035-1056. Dynamic analysis of an automatic
dynamic balancer for rotating mechanisms.
10.- C. H. Hwang and J. Chung 1999 JSME International
Journal 42, 265-272. Dynamic analysis of an automatic ball
balancer with double races.
Ing. Álvaro Aguilar Aguilar
Licenciatura: En Ingeniería Mecánica en la Universidad
Autónoma de Tlaxcala.
Maestría : Actualmente alumno del quinto semestre
de la Maestría en Ciencias en
Ingeniería Mecánica
(opción Diseño) del Instituto
Tecnológico de Puebla.
M.C. Marco Antonio Meraz Melo
Profesor de la Maestría en Ciencias en
Ingeniería Mecánica del Instituto
Tecnológico de Puebla.

