c) Integrador
Un integrador tiene por salida la integral de la
función
de entrada. El diagrama de
Bode de fases es constante en ?90º. Esto es lógico ya
que la integral de un seno es un menos coseno, que está
retrasado 90º respecto el seno.
 (4)
(4)
El diagrama de Bode de ganancias es una recta con
pendiente ?20 dB/década. La recta pasa por 0 dB en la
frecuencia de 1 rad/s.
 (fig.3)
(fig.3)
d) Derivador
Un derivador tiene por salida la derivada de la
función de entrada. El diagrama de Bode de fases es
constante en 90º. Esto es lógico ya que la derivada
de un seno es un coseno, que está adelantado 90º
respecto el seno.
 (5)
(5)
El diagrama de Bode de ganancias es una recta con
pendiente 20 dB/década. Igual que los integradores, la
recta pasa por 0 dB en la frecuencia de 1 rad/s.
 (fig.4)
(fig.4)
e) Polo simple
Un polo simple es un sistema de primer
orden con ganancia estática
igual a la unidad.
 (6)
(6)
Las ganancias y fases de la ecuación (6) se van a
particularizar para distintos casos. En la
ecuación
(7) se observa cómo la ganancia a bajas
frecuencias es aproximadamente 0 dB. Para altas frecuencias la
ganancia se parece a un integrador, una recta de pendiente ?20
dB/década, que pasa por 0 dB en la frecuencia igual a la
inversa de la constante de tiempo.
 (7)
(7)
En la ecuación (8) se observa cómo la fase
para bajas frecuencias es aproximadamente 0º y para altas
frecuencias ?90º.
 (8)
(8)
El diagrama de la (fig.5) corrobora el comportamiento
en ganancias y en fases.
 (fig.5)
(fig.5)
f) Cero simple
En este apartado se estudia el caso inverso del apartado
anterior.
![]() (9)
(9)
La ganancia a bajas frecuencias también comienzan
en 0 dB, ecuación (10). En cambio, para
altas frecuencias la ganancia se comporta como un derivador; una
recta de pendiente 20 dB/década, que pasa por 0 dB en la
frecuencia igual a la inversa de la constante de
tiempo.
 (10)
(10)
En fases, ecuación (11) para bajas frecuencias
toma valores
próximos a 0º y para altas frecuencias
aproximadamente 90º.
 (11)
(11)
El diagrama de Bode de la (fig.6) muestra el
comportamiento en ganancias y en fases.
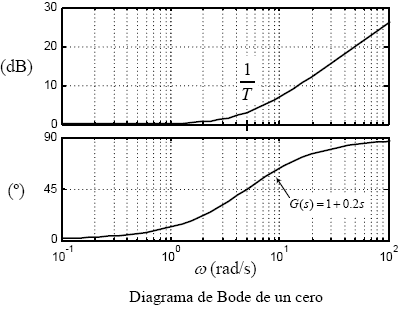 (fig.6)
(fig.6)
g) Polo doble
Un polo doble es un sistema de segundo orden con
ganancia estática igual a la unidad.

En la ecuación (8.14) se observa cómo la
ganancia para bajas frecuencias es aproximadamente 0 dB y para
altas frecuencias es una recta de pendiente ?40 dB/década
que pasa por 0 dB en la frecuencia igual a la frecuencia
natural.

En la ecuación (8.15) se observa cómo la
fase para bajas frecuencias es aproximadamente 0º y para
altas frecuencias ?180º.

El diagrama de Bode de la Fig. 8.8 muestra el
comportamiento en ganancias y en fases.
 (fig.7)
(fig.7)
En un rango de frecuencias próximo a la
frecuencia natural, el diagrama de Bode se comporta de forma
distinta en función del amortiguamiento. En la Figura (12)
anterior se observa cómo aparece un máximo en el
diagrama de ganancias. Se va a emplear la expresión (13)
para determinar la magnitud de dicho máximo y a qué
frecuencia se produce. En concreto, se
va a derivar la expresión del denominador para buscar un
mínimo ?que será un máximo de la
ganancia?.
 (15)
(15)
Si se estudiara el signo de la segunda derivada, se
comprobaría cómo la primera solución, para
frecuencia nula, se trata de un máximo del denominador y
por tanto un mínimo del diagrama de Bode. La otra
solución ωr, llamada frecuencia de
resonancia, es el máximo del diagrama de Bode que se
había observado.
Si se sustituye el valor de la
frecuencia de resonancia en la expresión de la ganancia
(13), se obtiene la magnitud del máximo, ecuación
(16), que se suele denominar pico de
resonancia.
 (15)
(15)
El fenómeno de la resonancia no siempre existe.
Sólo se da para un determinado rango de amortiguamientos.
En concreto, aquellos amortiguamientos que hacen positivo el
discriminante de la raíz cuadrada de la expresión
(15).
 (17)
(17)
En la ecuación (17) aparece el rango de
amortiguamientos con pico de resonancia. Se trata siempre de
sistemas
subamortiguados, aunque no todos los sistemas subamortiguados
poseen pico de resonancia. En la (Fig.8) se muestra cómo
varía el diagrama de Bode con el amortiguamiento. Cuanto
menor es el amortiguamiento mayor es el pico de resonancia y
más próximo está a la frecuencia natural.
También cuanto menor es el amortiguamiento más
brusco es el cambio de fases en torno a la
frecuencia natural.
 (fig.8)
(fig.8)
En el caso concreto de amortiguamiento igual a uno, es
decir, críticamente amortiguado y polo real doble, el
diagrama de ganancias pasa por ?6 dB en la frecuencia
natural.
h) Cero doble
Un cero doble es exactamente el caso inverso al
anterior.
 (18)
(18)
El desarrollo
matemático es análogo al del apartado anterior, por
lo que no se va a repetir. En el caso del cero doble
también existe el fenómeno de la resonancia,
sólo que se manifiesta en forma de mínimo en lugar
de un máximo en el diagrama de ganancias.
 (fig.9)
(fig.9)
i) Polo simple con parte real positiva
Un polo con parte real positiva constituye, en sí
mismo, un sistema inestable. Sin embargo, es posible representar
matemáticamente su diagrama de Bode.
![]() (9)
(9)
 (20)
(20)
 (21)
(21)
Su comportamiento en ganancias es igual que un polo con
parte real negativa. Esto se debe a que el cambio de signo no
afecto al módulo del número complejo. Sin embargo,
su comportamiento en fases es igual que un cero
simple.
 (fig.10)
(fig.10)
j) Cero simple con parte real positiva
Un cero con parte real positiva puede darse en un
sistema estable, pero su presencia ya se mostró
cómo convertía a una planta en un sistema de fase
no mínima.
 (22)
(22)
 (23)
(23)
 (24)
(24)
Su comportamiento en ganancias es exactamente igual que
un cero con parte real negativa, mientras que su comportamiento
en fases es igual que un polo simple.
 (fig.11)
(fig.11)
2) El Diagrama de Nyquist
- Definición.
El análisis de Nyquist, es un método de
la respuesta de frecuencia, es esencialmente un procedimiento
gráfico para determinar la estabilidad absoluta y relativa
de los sistemas de
control a circuito cerrado. La información sobre estabilidad está
disponible directamente de un gráfico de la función
de anillo abierto GH (U) de la respuesta de frecuencia, una vez
que el sistema de la regeneración se haya puesto en forma
canónica. Los métodos de
Nyquist son aplicables a los sistemas continuos y del tiempo
discreto de control, y el
desarrollo metodológico para el análisis de Nyquist
se presenta aquí para ambos tipos de sistemas, con un
cierto énfasis dado a los sistemas continuos, para los
propósitos pedagógicos.
Las técnicas
de Nyquist son también útiles para obtener la
información sobre funciones de la
transferencia de componentes o sistemas de datos
experimentales de la respuesta de frecuencia. El diagrama polar
puede ser representado gráficamente directamente de
medidas sinusoidales del estado
constante en componer de los componentes función de anillo
abierto de la transferencia. Esta característica es muy
útil en la determinación de las
características de la estabilidad del sistema cuando las
funciones de la transferencia de los componentes del lazo no
están disponibles en forma analítica, o cuando los
sistemas físicos deben ser probados y ser evaluados
experimental.
El diagrama de Nyquist permite predecir la estabilidad y
el funcionamiento de un sistema de lazo cerrado observando su
comportamiento de lazo abierto. El criterio de Nyquist se puede
utilizar para los propósitos de diseño
independientemente de la estabilidad de lazo abierto (recuerde
que los métodos de diseño de Bode asumen que el
sistema es estable en lazo abierto). Por lo tanto, utilizaremos
este criterio para determinar la estabilidad de lazo cerrado
cuando los diagramas de Bode
muestran la información de un modo quizas confuso. La
siguiente le ayudará a visualizar la
relación entre el diagrama de Bode y el diagrama de
Nyquist.
El diagrama de Nyquist es básicamente un diagrama de G(j *
w) donde G(s) es la función de lazo abierto de
transferencia y W es un vector de frecuencias que incluye el
semiplano derecho. En el dibujo se
consideran tanto frecuencias positivas como negativas (de cero al
infinito) Representaremos frecuencias positivas en rojo y
negativas en verde. El vector de frecuencias usado para trazar el
diagrama de Nyquist luce generalmente como se muestra (si usted
puede imaginar el diagrama estirado hacia el
infinito):

Sin embargo, si tenemos polos de lazo abierto o ceros en
el eje jw, G(s) no estara definido en esos puntos, y debemos
"esquivarlos" cuando estamos trazando el contorno. Tal contorno
quedaria como sigue:

En el criterio de Nyquist se emplea un planteamiento
distinto al utilizar los conceptos del estado permanente ceno en
tal correspondientes a este estudio. Originalmente lo
formuló en 1932 Harry Nyquist de los Bell Telephone
Laboratories. Es importante observar que su utilidad en la
práctica se relaciona con el hecho de que se puede aplicar
a través de mediciones senoidales de rutina que es posible
efectuar en el laboratorio.
La operación básica al aplicar el criterio
de Nyquist es un Mapeo del plano S al plano F(s). Este documento
presenta el criterio de estabilidad de Nyquist y sus fundamentos
matemáticos. Sea el sistema de lazo cerrado que se ve en
la Fig. No. 1. La función transferencia de lazo cerrado es
:

Se tendrá estabilidad cuando todas las
raíces de la ecuación
característica
1 + G(S)H(S) = 0
estén en el semiplano izquierdo s. El criterio de
estabilidad de Nyquist relaciona la respuesta de frecuencia de
lazo abierto G(jω) H(jω) a la cantidad de ceros y
polos de 1 + G(s) H(s) que hay en el semiplano derecho s. Este
criterio debido a H. Nyquist es ϊtil en ingeniería de control porque se puede
determinar gráficamente de las curvas de respuesta de lazo
abierto la estabilidad absoluta del sistema de lazo cerrado, sin
necesidad de determinar los polos de lazo cerrado. Se pueden
utilizar para el
análisis de estabilidad las curvas
de respuesta de frecuencia de lazo abierto obtenida
analíticamente o experimentalmente. Esto es muy
conveniente porque al diseñar un sistema de control
frecuentemente sucede que para algunos componentes no se conoce
la expresión matemática
y solo se dispone de datos de su característica de
respuesta de frecuencia.
El criterio de estabilidad de Nyquist esta basado en un
teorema de la
teoría de las variables
complejas. Para entender el criterio primero se han de tratar los
con tornos de
transformación en el plano complejo.
Se supone que la función transferencia de lazo
abierto G(s) H(s) es representable como una relación de
polinomios en s. Para un sistema físicamente realizable,
el grado del polinomio denominador de la función
transferencia de lazo cerrado, debe ser mayor o igual al del
polinomio numerador. Esto significa que el limite de G(s) H(s) es
cero o una constante para cualquier sistema físicamente
construible, al tender s hacia infinito.
Estudio preliminar.
La ecuación característica del sistema
es:
F(s) = 1 + G(s)H(s) = 0
Se ha de demostrar que a un camino cerrado continuo dado
en el plano s que no pasa por ningún punto singular,
corresponde una curva cerrada en el plano F(s).
La cantidad y sentido de lazos o rodeos alrededor del
origen en el plano F(s) por una curva cerrada, juega un papel
importante en lo que sigue, pues mas adelante se ha de relacionar
la cantidad y sentido de lazos o rodeos con la estabilidad del
sistema.
Sea, por ejemplo, la siguiente función
transferencia de lazo abierto:
![]()
La ecuación caracteristica es .
![]() =
=
0
La función F(s) es analítica en cualquier
parte del plano s, excepto en sus puntos singulares. Para cada
punto de analiticidad en el plano s, corresponde un punto en el
plano F(s). Por ejemplo, Si s = 1 + 2j, entoces F(s) es
:
![]()
Entonces el punto s = 1 + 2j en el plano s se transforma
en el punto 1.1 2 ? 5,77j en el plano F(s).
Del análisis precedente, se puede ver que el
sentido en el que se rodea el origen en el plano F(s) depende de
si el contorno en el plano s incluye un polo o un cero. Se hace
notar que la ubicación de un polo o cero en el plano s,
sea en la mitad derecha o izquierda del plano s, no produce
ninguna diferencia, pero si la produce el rodeo de un polo o un
cero. Si el contorno del plano s incluye k ceros y k polos (k =
0, 1, 2, …), es decir igual cantidad de cada uno, la
correspondiente curva cerrada en el plano F(s) no encierra el
origen del plano F(s). La discusión precedente es una
explicación gráfica del teorema de
representación, que es la base del criterio de estabilidad
de Nyquist.
Aplicación del teorema de la
representación al análisis de estabilidad
de sistemas de lazo cerrado
Para analizar la estabilidad de sistemas de control
lineal, se hace que el contorno cerrado del plano s
abarque todo el semiplano derecho s. El contorno consiste en todo
el eje ω desde (ω = – ∞ hasta ω =
+∞) , y un paso semicircular de radio infinito en
el semiplano s derecho. Este contorno recibe el nombre de
recorrido de Nyquist. (El sentido del mismo es
horario.) El recorrido de Nyquist abarca todo el semiplano
derecho de s y contiene todos los ceros y polos de 1 + G(s)H(s)
con partes reales positivas. (Si no hay ceros de 1 + G(s)H(s) en
el semiplano derecho de s, no hay polos de lazo cerrado alli y el
sistema es estable.) Es necesario que el contorno cerrado o
recorrido de Nyquist no pase por ningún polo o cero de 1 +
G(s)H(s). Si G(s) tiene un polo o polos en el origen del plano s,
se hace indeterminada la representación del punto s = 0.
En esos casos se evita el origen efectuando un desvio alrededor
de él. (Más adelante se efectúa una
discusión detallada sobre este caso especial.) Si se
aplica el teorema de la representación al caso especial en
que F(s) es igual a 1 + G(s)H(s) se puede afirmar lo siguiente:
si el contorno cerrado en el plano s contiene todo el semiplano s
derecho, como se muestra en la Fig. 3, la cantidad de ceros en el
semiplano derecho de la función F(s) = 1 + G(s)H(s) es
igual a la cantidad de polos de la función F(s) = 1 +
G(s)H(s) en el semiplano derecho de s mas la cantidad de rodeos
completos horarios al origen del plano 1 + G(s)H(s) de la curva
cerrada correspondiente en este último plano. Debido a la
condición supuesta de que
lim [1 + G(s)H(s)] =
la función 1 + G(s)H(s) permanece constante
mientras s recorre el semicírculo de radio infinito.
Debido a esto, se puede determinar si el lugar de 1 + G(s)H(s)
Fig. 3.

Contiene o no el origen del plano 1 + G(s)H(s)
analizando tan sólo una parte del contorno cerrado del
plano s, el eje ωj. Si hay rodeos al origen, se producen
únicamente cuando el punto representativo pasa de
?j∞ a +j∞ a lo largo del eje ωj, siempre que no
haya ceros ni polos sobre el eje
ωj.
Nótese que la porción del contorno de 1 +
G(s)H(s) desde (ω = – ∞ hasta ω =
+∞), es simplemente 1 + G(ωj)H(ωj). Como 1 +
G(ωj)H(ωj) es el vector suma del vector unitario y el
vector G(ωj)H(ωj), el tιrmino 1 +
G(ωj)H(ωj) es igual al vector que va
desde el punto – 1 + 0j hasta el extremo del vector
G(ωj)H(ωj). Circunscribir el origen por el grafico 1
+ G(ωj)H(ωj) equivale a hacerlo con el punto -1 +0j
por el lugar de G(ωj)H(ωj). Entonces se puede
estudiar la estabilidad de un sistema de lazo cerrado analizando
los rodeos del punto – 1 + 0j por el lugar de
G(ωj))H(ωj). Se puede determinar la cantidad de giros
que incluyen el punto – 1 + 0j trazando un vector desde el punto
– 1 + 0j hasta el lugar de G(ωj)H(ωj), comenzando en
(ω = – ∞, pasando por (ω = 0, y
llegando hasta ω = + ∞ mientras se cuenta la cantidad
de rotaciones horarias del vector.
El trazado de G(jω)H(jω) para el recorrido
de Nyquist es inmediato. La representaciσn del eje negativo
jω es la imagen
simétrica del eje positivo jω respecto al eje real.
Es decir, el diagrama de G(jω)H(jω) y el de
G(jω)H(-jω) son simιtricos respecto al eje real.
El semicνrculo de radio infinito se transforma en el origen
del plano GH o en un punto sobre el eje real del plano
GH.
En la exposición
precedente, se supuso que G(s)H(s) es la relación entre
dos polinomios en s. De modo que ha quedado fuera del
análisis el retardo de transporte
e-T*s.

Sin embargo, a sistemas con retardo de transporte se les
aplica un estudio similar, aunque no se incluye aqui su
demostración. Se puede determinar la estabilidad de un
sistema con retardo de transporte examinando en las curvas de
respuesta de frecuencia la cantidad de veces que se rodea al
punto – 1 + j0, Como en el caso de un sistema cuya función
transferencia de lazo abierto es una relación entre dos
polinomios en s.
3)
Diagrama de Black ? Nichols:
- Definición.
Este tipo de representación se basa en el hecho
de colocar sobre un mismo plano el módulo y la fase de la
función de transferencia a partir de sus dos gráficas separadas. Se usa mucho si los
diseños y cálculos se realizan a mano, pero en la
actualidad, debido al uso de ordenadores, este tipo de diagrama
está perdiendo importancia. Aún así veremos
algún ejemplo.
%Ejemplo
num = [-4 48 -18 250 600];
den = [1 30 282 525 60];
H = tf(num,den)
Nichols(H);ngrid

Estabilidad según Nichols:
La traza de magnitud- fase es otra forma de
gráfica en el dominio de la
frecuencia, que tiene ciertas ventajas de análisis y
diseño en el dominio de la frecuencia. La traza de
magnitud-fase de una función de transferencia L(jw) se
hace en el valor absoluto de |L(jw)| (dB) contra <L(jw)
(grados).
El punto crítico es la intersección del
eje o dB y el eje -180º.
- El cruce de fase es donde el lugar geométrico
intercepta al eje -180º. - El cruce de ganancia es donde el lugar
geométrico intercepta al eje 0 dB. - El margen de ganancia es la distancia vertical en dB
medida del cruce de fase al punto crítico. - El margen de fase es la distancia horizontal en
grados medida del cruce de ganancia al punto
crítico.
Otra ventaja de emplear la traza de magnitud ? fase es
que para sistemas con realimentación unitaria, los
parámetros del sistema en lazo cerrado, tales como Mr,
r y BW se pueden determinar de la traza con la ayuda del
lugar geométrico de M constante. Estos parámetros
de desempeño en lazo cerrado no están
representados en las trazas de Bode de la función de
transferencia de la trayectoria directa de un sistema con
realimentación unitaria.
Lugar geométrico de M constante en el plano
G(jw)
El pico de resonancia Mr y el ancho de banda BW son
difíciles de obtener para sistemas de orden superior, y
las trazas de Bode proveen información sobre el sistema en
lazo cerrado sólo en la forma de margen de ganancia y
margen de fase. Es necesario desarrollar un método
gráfico para la determinación de estos
parámetros empleando la función de transferencia de
la trayectoria directa de G(jw). Como veremos a
continuación, el método es en directo aplicable
sólo a sistemas con realimentación unitaria,
aún cuando con algunas modificaciones también se
puede aplicar a sistemas con realimentación no
unitaria.
Consideremos que G(s) es la función de
transferencia de la trayectoria directa de un sistema con
realimentación unitaria. La función de
transferencia de lazo es:
![]()
Para un estado senoidal permanente hacemos s=jw
tenemos:
![]()
Así el módulo de M será:

Si consideramos M(jw)=M (por simplificar)
tenemos:
![]()
y al operar nos queda:

Para un valor dado de M, esta ecuación representa
un círculo de centro  y radio
y radio ![]() .
.
Cuando M toma diferentes valores la ecuación
anterior describe en el plano G(jw), una familia de
círculos que se llaman lugar geométrico de M
constante, o círculos de M constante; éstos son
simétricos con respecto a la línea M =1 y al eje
real.
Gráficamente, la intersección de la curva
G(jw) y el círculo M constante da el valor de M en la
frecuencia correspondiente sobre la curva de G(jw). Si se quiere
mantenerle valor de Mr menor que cierto valor, la curva G(jw) no
debe interceptar al círculo correspondiente de M en
cualquier punto, y al mismo tiempo no debe encerrar al punto
(-1,j0). El círculo M constante con el menor radio que es
tangente a la curva G(jw) da el valor de Mr, y la frecuencia de
resonancia ![]() se lee
se lee
del punto tangente sobre la curva G(jw). El BW se encuentra en la
intersección de la curva G(jw) y el lugar
geométrico M =0.707.
Lugar geométrico de fase constante en el plano
G(jw)
El lugar geométrico de fase constante de un
sistema en lazo cerrado se puede graficar en el plano G(jw9 a
través de un método similar al usado para graficar
el lugar geométrico de M constante. En general, la
información de fase del sistema en lazo cerrado rara vez
se utiliza en el análisis y diseño, ya que la
información sobre Mr, ![]() , y BW se obtiene de la curva de magnitud.
, y BW se obtiene de la curva de magnitud.
Los lugares geométricos de fase constante se
llaman círculos de N constante y se describen por la
ecuación:
![]()
La carta de
Nichols:
Una de las mayores desventajas al trabajar en
coordenadas polares de la traza de Nyquist de G(jw) es que la
curva ya no retiene su forma original cuando una
modificación simple tal como el cambio de ganancia de lazo
se hacen al sistema. Frecuentemente, en situaciones de introducir
controladores al sistema. Esto requiere una reconstrucción
completa de la traza de Nyquist de la G(jw) modificada. APRA
el trabajo de
diseño que involucra a Mr y BW como especificaciones, es
más conveniente trabajar con la traza de magnitud-fase
G(jw), ya que cuando se altera la ganancia de lazo, la curva
G(jw) completa se corre hacia arriba o hacia abajo en forma
vertical, sin distorsión. Cuando las propiedades de fase
de G(jw) se cambian de forma independiente, sin afectar la
ganancia, la traza de magnitud-fase se afecta sólo en
dirección horizontal.
Por la razón anterior, el lugar geométrico
de M constate en las coordenadas polares se transfiere a las
coordenadas magnitud-fase, y el lugar geométrico
resultante forma una carta de Nichols.
Veamos un ejemplo:
![]()
Recordemos que la simulación
hay que hacerla con realimentación unitaria.
Probaremos para varios valores de K: K = 7.348, K =
14.5, K = 181.2, K = 273.57.
%Ejemplo
s=tf('s') %defino la función de transferencia
de la planta
num=15000000
den=s*(s+400.26)*(s+3008)
Planta=(num/den)
open1=7.348*planta %creo los cuatro sistemas en lazo
abierto con los open2=14.5*planta distinta K
open3=181.2*planta
open4=273.57*planta
close1=feedback(open1,1) %creo cuatro sistemas en lazo
cerrado close2=feedback(open2,1) mediante los sistemas en lazo
abierto definidos close3=feedback(open3,1) antes
close4=feedback(open4,1)
nichols(close1,'b',close2,'r',close3,'g',close4,'y') %pinta
los diagramas de Nichols de los cuatro sistemas

Si ahora analizamos su respuesta al
escalón:
step(close1,?b?) step(close2,'r')


step(close3,?g?) step(close4,'y')


Se puede observar que tanto el primer sistema como el
segundo son estables, el tercero es marginalmente estable (su
diagrama de Nichols pasa por el punto (-1,j0)), y el cuarto es
inestable.
4) SISTEMA DE
FASE MÍNIMA:
- Definición
Hemos visto que un sistema es de fase mínima
cuando todos sus polos y ceros están en el semiplano
izquierdo, si tiene algún cero en el semiplano derecho se
dice que es de fase no mínima y si tiene algún polo
en este último semiplano se tratará de un sistema
inestable.
Ambos tipos de sistemas tienen la misma
característica de amplitud pero no de ángulo de
fase, ya que los sistemas de fase no mínima tienen
un atraso grande de fase a altas frecuencias.
Por ejemplo:

Las curvas de ángulo de fase son:

Una forma experimental de determinar si un sistema es
de fase mínima o no, es a partir del diagrama de Bode.
Así, si un sistema cumple las dos siguientes
condiciones, será de fase mínima:
1) La pendiente de la curva del logaritmo de la
amplitud cuando w® ¥ es -20(q-p) dB/déc, donde
'q' y 'p' son los grados de los polinomios denominador y
numerador de la función de transferencia
respectivamente.
2) El ángulo de fase en w® ¥ es
-90º(q-p).
Los sistemas con retardo son sistemas de fase no
mínima porque tienen un atraso de fase excesivo a altas
frecuencias:

El logaritmo de la amplitud del retardo es 0dB, sin
embargo el ángulo de fase varía linealmente con
la frecuencia como podemos ver en el siguiente
gráfico:

Efecto de los ceros.
Pese a que en las secciones anteriores se ha hecho
énfasis en el efecto que tiene sobre la respuesta natural
la ubicación de los polos en el plano, no debe
desconocerse que los ceros también influyen en la
respuesta.
Supóngase un sistema continuo de segundo orden,
con un cero real:
| (4.10) |
La respuesta al escalón del sistema definido por
(4.10)
es :
| (4.11) |

Es importante resaltar que para ceros en el semiplano
derecho (este es el caso ![]() en la figura
en la figura
4.28) la respuesta al escalón
presenta en sus inicios valores de signo contrario a los de la
respuesta de estado estacionario; este fenómeno, conocido
como subpico (en inglés
undershoot) puede llegar a ser muy peligroso en algunos
sistemas físicos, y constituye una gran dificultad para su
control.
Los sistemas que no poseen ceros en el semiplano
derecho, se conocen como sistemas de fase mínima, o
simplemente minifase
La presencia de subpicos ante una entrada escalón
es fácil de demostrar para un sistema de segundo orden con
polos reales y un cero real, tal como
| (4.12) |
La respuesta al escalón será:

L

5)
Márgenes de ganancia y de fase.
- márgenes de ganancias de a través de
la carta de
nichols.
- Compensación del factor de
ganancia
Se desea que la máxima ganancia del sistema
realimentado dado por la siguiente ecuación, sea de
2db:

En primer lugar se realiza la grafica de magnitud contra
fase del sistema:

Fig 4. Representación de magnitud Vs
fase
Después de esto esta misma grafica se sobrepone
en la Carta de Nichols, de la misma forma como se hizo en el
ejemplo anterior:

Fig 5. Superposición sobre la
carta de Nichols
A partir de esta superposición se puede apreciar
que la máxima amplitud del sistema se da a una frecuencia
de 1.1Hz, y cuyo valor es aproximadamente 1db.
Como lo que se desea es que la máxima amplitud
del sistema sea de 2db, la grafica de magnitud vs fase de
la función de transferencia se desplaza hacia arriba hasta
lograr que esta curva sea tangente al contorno M constante de 2db
(Ver figura 6).
En la grafica 6 se aprecia el desplazamiento que se le
tuvo que hacer a la grafica para lograr su tangencia a la curva M
de 2db, la medida de ese desplazamiento fue de aproximadamente
4.5db en dirección positiva. Con este valor se puede
encontrar el valor de la ganancia adicional que se debe sumar al
sistema original para que su respuesta cumpla con las
especificaciones del circuito.

Fig 6. Desplazamiento para la
compensación de ganancia
Para determinar el valor de la ganancia del sistema
compensado se toma la siguiente ecuación:

Donde Ki es el factor de ganancia del sistema
original, Kb es el nuevo factor de ganancia que se
desea hallar y es el desplazamiento (en db) que tuvo la
grafica magnitud contra fase. Para los valores
del ejercicio, ki=2.04 y =4.5db. Despejando
kb para los valores dados se tiene que el nuevo factor
de ganancia es de 3.43
Entonces la función de transferencia del sistema
ya compensado es:

De la grafica 6 se puede sacar la grafica magnitud
contra fase del nuevo sistema realimentado:

Fig 7. Respuesta del circuito.Compensado
y sin compensar
En el anterior grafico se puede observar el cambio de la
respuesta en frecuencia del sistema compensado y del original,
viéndose claramente que el sistema compensado cumple con
una ganancia máxima de 2db. Sin embargo también se
observa que la frecuencia de resonancia también cambia con
la compensación de ganancia.
La respuesta en frecuencia de lazo cerrado con la
ganancia ajustada, puede tener una frecuencia de resonancia muy
diferente a la que se tenia con el sistema original (como se
observa en la grafica anterior), y esto puede que no cumpla con
las especificaciones que se quieren para el sistema. El siguiente
paso en el diseño del sistema es el de compensar el
sistema para mejorar la respuesta espectral.
- Márgenes de fase y de ganancias en bode y
nyquist
El diagrama de Nyquist, además de permitir
determinar si un sistema es estable o inestable, nos puede
indicar el grado de estabilidad de un sistema, que es lo que se
conoce como estabilidad relativa.
Si, por ejemplo, tenemos un sistema con la siguiente
función de transferencia de lazo abierto:

Al aumentar la ganancia k, el diagrama de Nyquist se va
abriendo, es decir, se aproxima al punto crítico
-1+j0:

– Para k = k1: el sistema es
estable.
– Para k = k2: el sistema es estable pero
más cercano al punto crítico.
– Para k = kcrítica: el sistema se
convierte en oscilante ya que tendremos un polo en el eje
jw.
– Para k > kcrítica: el sistema es
inestable y rodea al punto -1+j0.
El grado de estabilidad relativa de un sistema se define
con dos conceptos denominados margen de ganancia y margen de
fase, que a continuación vemos:
a) Margen de ganancia
El margen de ganancia (Mg) es el inverso de
|G(jw)| a la frecuencia de cruce o de transición de
fase(w1), que es a la cual el ángulo de fase
de la función de transferencia en lazo abierto es
-180º. Si la realimentación es unitaria (H(jw)=1),
podemos expresarlo como:

Un margen de ganancia positivo (en decibelios)
significa que el sistema es estable; y si es negativo (en dB),
será inestable. Si es nulo (en dB), el sistema es
críticamente estable, es decir, tiende a la
inestabilidad.
Para un sistema de fase mínima estable, el
margen de ganancia indica en cuánto se puede incrementar
la ganancia antes de que el sistema se haga
inestable.
Para un sistema de fase mínima inestable, el
margen de ganancia nos dice en qué cantidad hay que
reducir la ganancia para hacer al sistema estable.
b) Margen de fase
Es la cantidad de retardo de fase adicional necesaria
para que el sistema quede al borde de la inestabilidad a la
frecuencia de corte o de transición de ganancia, que es
aquella frecuencia para la cual |G(jw)| es la unidad. El margen
de fase Mf es 180º más el ángulo
de fase de la función de transferencia de lazo
abierto a la frecuencia de cruce de ganancia:
![]()
En el diagrama de Nyquist, se puede trazar una recta
desde el origen al punto de cruce de la curva de Nyquist con el
círculo de radio unidad. El ángulo desde el eje
real negativo a esta recta es el margen de fase.

Para que un sistema de fase mínima sea estable,
el margen de fase debe ser positivo; si es negativo, el sistema
será inestable.
Para el caso de los sistemas de fase no mínima,
se cumple que serán estables si los márgenes de
ganancia y fase son negativos.
c) Margen de ganancia y de fase en el
diagrama de Bode
En el diagrama de Bode, el margen de ganancia se
entiende como el número de decibelios que se puede
aumentar la ganancia del sistema hasta hacer que la curva de
amplitud corte al eje de frecuencias, a la frecuencia en el que
el ángulo de fase es -180º.
El margen de fase es el número de grados que le
faltan a la curva del ángulo de fase para cortar a la
horizontal de desfase -180º cuando la curva de amplitudes
corta al eje de frecuencias (0 dB).

En la práctica, para que un sistema de control
tenga un funcionamiento adecuado, el margen de ganancia debe
ser superior a 6dB y el margen de fase estar entre +30º y
+60º. Con estos márgenes, queda garantizada la
estabilidad del sistema a pesar de que las constantes de tiempo
de los componentes varíen dentro de ciertos límites.
EJERCICIOS DE APLICACIÓN
- Ejercicio del diagrama de bode
- Considere el sistema que se muestra en el que una
señal de entrada x(t) es procesada por un sistema con
función de transferencia G(s) para obtener y(t) que
luego es amplificada por una ganancia K para obtener
z(t).

La función de transferencia del sistema
es:
y
- Dibuje el Diagrama de Bode de Magnitud y determine el
ancho de banda y el punto de cruce de la ganancia - ¿Qué sucede con el ancho de banda y el
punto de cruce si la ganancia se aumenta en 10 y se disminuye
en 10? - ¿En qué caso es sistema es más
rápido?
1.-La función de transferencia puede ser
reescrita como:

Por lo que en el diagrama de Magnitud de Bode vamos a
tener cambios de pendiente en w=1 y w=10.
Quedandonos el siguiente diagrama:

-Para hallar el punto de cruce igualamos la
ecuación de la recta de pendiente -20 a "0".
Ec. de la recta:
20log(5)-20log(w)=0, la solución a esta
ecuación es w=5.
-Para hallar el ancho de banda igualamos la
ecuación de la recta dependiente -20 a
20log(5)-3
20log(5)-20log(w)=20log(5)-3, por lo tanto 20log(w)=3, y
esta igualdad se
cumple para w=1.413 que corresponde al ancho de banda.
Consideramos para el primer caso una ganancia 10,
entonces la funcion de transferencia quedaría:

El diagrama de Bode es muy parecido al de la parte A,
con la diferencia de que este último empieza en 33.98 dB.
El ancho de banda es EL MISMO. Esto se debe a que la caida de 3
dB con relacion a la ganancia en o se da en el mismo punto w=1.41
. Para el punto de corte, en éste caso debemos usar la
ecuación de la recta de pendiente 13.98-60log(w/10)=0,
w=16.98
Para el segundo caso, tomamos la ganancia reducida en 10
veces:

De nuevo el diagrama es muy parecido, pero en esta
ocasión comienza en el semiplano inferior,
específicamente en -6dB. La frecuencia de ancho de banda
es la misma(w=1.41). Este diagrama no corta con el punto de
ganancia 0, ya que esta es siempre negativa.
Al comparar los diagramas de fase se observa que el
más rápido es el de la ganancia aumentada en 10, ya
que para frecuencias mas altas todavía tiene una ganancia
considerable cuando los otros ya la han bajado en gran
proporción.
2) Ejercicio del diagrama de nyguist.
Considere el sistema con la siguiente función de
transferencia en lazo abierto:
![]()
Determine la estabilidad del sistema y el diagrama de
nyguist para dos casos:
(1) la ganancia K es pequeña, y
(2) K es grande.
Las trazas de Nyquist de la función de
transferencia en lazo abierto para un valor pequeño de
K y un valor grande de K aparecen en la figura que
tenemos mas adelante. El número de polos de G(s)H(s) en el
semiplano derecho del plano s es cero. Por tanto, para que este
sistema sea estable, es necesario que
N = Z = 0 o que el lugar geométrico G(s)H(s) no
encierre el punto -1 + jo.

3) Ejercicio del diagrama de nichols
Con las reglas de Nichols, determinar ![]() y
y ![]() para el sistema de control demostrado en
para el sistema de control demostrado en
el siguiente figura:

Para este problema, el cómputo será hecho
sin trazar el diagrama de bode; sin embargo, el lector puede
desear hacer el problema con tal diagrama. Primero obtenemos la
frecuencia de cruce aplicando el criterio de la estabilidad de
bode:
![]()
Los radianes del valor 57.3 los convertiremos a
los grados. Solucionar esta ecuación por ensayo y error
da para la frecuencia de cruce, wco = 2 rad/Min. El cociente de
la amplitud (AR) en la frecuencia de cruce para el lazo abierto
puede ser escrito

Donde hemos utilizado Eq.

Para el sistema de primer orden y el hecho de que el
cociente de la amplitud para un retraso del transporte es 1.
Según el criterio de bode, el AR es 1.0 en la frecuencia
de cruce cuando el sistema está en el borde de la
inestabilidad. Insertando AR = 1 en la ecuación antedicha
y solucionando para K, da K, = 2.24. De las reglas de Nichols de
la tabla 17.1:

Obtenemos:
![]()
Y
![]()
4) Ejercicio de sistemas de fase
mínima
Supóngase un sistema continuo de segundo orden,
con un cero real:
| (4.10) |
La respuesta al escalón del sistema definido por
(4.10)
es :
| (4.11) |
La figura
4.28 muestra la gráfica de (4.11),
para tres valores distintos de ![]() es decir, lo que se está modificando es la
es decir, lo que se está modificando es la
posición del cero de la función de transferencia.
Alli puede verse que la ubicación del cero afecta
directamente la forma de la respuesta.

Más importante aún es resaltar que para
ceros en el semiplano derecho (este es el caso ![]() en la figura
en la figura
4.28) la respuesta al escalón
presenta en sus inicios valores de signo contrario a los de la
respuesta de estado estacionario; este fenómeno, conocido
como subpico (en inglés undershoot) puede
llegar a ser muy peligroso en algunos sistemas físicos, y
constituye una gran dificultad para su control.
Los sistemas que no poseen ceros en el semiplano
derecho, se conocen como sistemas de fase mínima, o
simplemente minifase.
La presencia de subpicos ante una entrada escalón
es fácil de demostrar para un sistema de segundo orden con
polos reales y un cero real, tal como
| (4.12) |
La respuesta al escalón será:


CONCLUSIÓN
Este trabajo se
realizo con la finalidad de ampliar conocimientos acerca de los
diagramas desarrollados anterior mente, por ejemplo el de Bode se
uso con éxito
en la segunda guerra
mundial y contribuyo al rápido desarrollos de
servomecanismos para dispositivos electrónicos de control
de disparo, como seguimiento se toco varios puntos de interés
tales como: ganancias del sistema, retraso en el tiempo,
integrador, derivador. También se trato el diagrama de
Nyquist. Este criterio que tiene el mismo objetivo que
el de Routh-Hurwitz pero con la diferencia de que se emplea un
planteamiento distinto al utilizar los conceptos del estado
permanente ceno en tal correspondientes a este
estudio.
También nos referimos al diagrama de Nichols que
este mejoro el teorema de Nyquist y Bode. Este presenta la
ventaja de mostrar en una sola grafica la fase y la magnitud de
la función que se analiza.
Como se puede observar tocamos en amplia margen los
lineamientos y objetivos que
se trazaron para su invastigacion , esperamos que sea explicito y
de total comprensión así como también se
halla cubierto todas las expectativas expuestas.
Bibliografía
- Libros.
- Schaum. (1990). Teoría y problemas
de regeneración y sistemas de control. (2da Edición). California: MC GRAW-Hill.
(Paginas: 245-247)
- Ogata K. (1998). Ingeniería de Control
moderna. (3era Edición). México: Prentice-Hall Hispanoamericano.
(Paginas: 532,533)
- Goughanowr. (1991). Process Systems Analysis and
Control. (2da Edición). New York: MC GRAW-HILL.
(Paginas: 209, 233-234)
- Arias, F. (1997). El proyecto de
investigación.
(2da Edición). Caracas: Episteme. (Paginas:
60-76)
- Autor Institucional.
- Universidad de Navarra. (2004). Control de sistemas
Continuos. (1er Edición). San Sebastián: Jorge
Juan Gil Nobajas y Ángel Rubio Díaz. (Paginas:
57-67)
- Páginas Web.
- Universidad Nacional de Asunción. (2007).
Análisis y Diseño por Respuesta de
Frecuencia. [On-Line]. Disponible en:
http://www.ing.una.py/DIREC_PPAL/ACADEMICO/APOYO/CONTROL%20CON%20SCILAB/freq/nyq.html
obtenida el 13 Feb 2007 06:38:02 GMT. - Monografías.com. (1997). Criterio de
estabilidad de Nuquist. [On-Line]. Disponible en:http://www.monografias.com/trabajos12/critestb/critestb.shtml
obtenida el 25 Mar 2007 22:04:35 GMT - Universidad del País Vasco. (2007).
Efectos de los Ceros. Sistemas de Fase Mínima.
[On-Line]. Disponible en:
http://www.ehu.es/iswezraa/ErregAut/mirror/www.virtual.unal.edu.co/orden/node6.html
obtenida el 19 Ene 2007 20:27:41 GMT. - Universidad de
Valladolid. (2007). Márgenes de
ganancias de a través de la carta de nichols.
[On-Line]. Disponible en:
www.isa.cie.uva.es/proyectos/servos/info/teoria/tema5_teoria.htm
obtenida el 18 Ene 2007 10:37:11 GMT.
- Universidad Nacional de Asunción. (2007).
Integrante:
Tiapa Jonatan
REPUBLICA BOLIVARIANA DE VENEZUELA
MINISTERIO DE LA DEFENSA
UNIVERSIDAD NACIONAL ESPERIMENTEL DE LA FAN
NUCLEO-ZULIA
Maracaibo, abril del 2007
 Página anterior Página anterior |   Volver al principio del trabajo Volver al principio del trabajo | Página siguiente  |





