Indice
1.
Introducción
2. Producción de una onda
sonora
3. La velocidad del
sonido.
4. Vibración Forzada y
Resonancia.
5. Ondas sonoras.
6. Tono y Timbre
7. Interferencia y
pulsaciones.
8. Efecto Doppler.
Cuando se produce una perturbación
periódica en el aire, se originan
ondas sonoras
longitudinales. Por ejemplo, si se golpea un diapasón con
un martillo, las ramas vibratoria emiten ondas longitudinales. El
oído, que actúa como receptor de estas ondas
periódicas, las interpreta como sonido.
El término sonido se usa de dos formas distintas.
Los fisiólogos definen el sonido en término de las
sensaciones auditivas producidas por perturbaciones
longitudinales en el aire. Para ellos, el sonido no existe en un
planeta distante. En física, por otra
parte, nos referimos a las perturbaciones por sí mismas y
no a las sensaciones que producen.

Sonido es una onda mecánica longitudinal que se propaga a
través de un medio elástico.
En este caso, el sonido existe en ese planeta. El
concepto de
sonido se usará en su significado
físico.
2. Producción de una onda
sonora.
Deben existir dos factores para que exista el sonido. Es
necesaria una fuente de vibración mecánica y
también un medio elástico a través del cual
se propague la perturbación. La fuente puede ser un
diapasón, una cuerda que vibre o una columna de aire
vibrando en un tubo de órgano. Los sonidos se producen por
una materia que
vibra. La necesidad de la existencia de un medio elástico
se puede demostrar colocando un timbre eléctrico dentro de
un frasco conectado a una bomba de vacío. Cuando el timbre
se conecta a una batería para que suene continuamente, se
extrae aire del frasco lentamente. A medida que va saliendo el
aire del frasco, el sonido del timbre se vuelve cada vez
más débil hasta que finalmente ya no se escucha.
Cuando se permite que el aire penetre de nuevo al frasco, el
timbre vuelve a sonar. Por lo tanto, el aire es necesario para
transmitir el sonido.
Ahora estudiemos más detalladamente las ondas
sonoras longitudinales en el aire que proceden de una fuente que
producen vibraciones. Una tira metálica delgada se sujeta
fuertemente en su base, se tira de uno de sus lados y luego se
suelta. Al oscilar el extremo libre de un lado a otro con
movimiento
armónico simple, se propagan a través del aire una
serie de ondas sonoras longitudinales periódicas que se
alejan de la fuente. Las moléculas de aire que colindan
con la lámina metálica se comprimen y se expanden
alternativamente, transmitiendo una onda. Las regiones densas en
las que gran número de moléculas se agrupan
acercándose mucho entre sí se llaman compresiones.
Son exactamente análogas a las condensaciones estudiadas
para el caso de ondas longitudinales en un resorte en espiral.
Las regiones que tienen relativamente pocas moléculas se
conocen como rarefacciones. Las compresiones y rarefacciones se
alternan a través del medio en la misma forma que las
partículas de aire individuales oscilan de un lado a otro
en la dirección de la propagación de la
onda. Puesto que una compresión corresponde a una
región de alta presión y una rarefacción
corresponde a una región de baja presión, una onda
sonora también puede representando trazando en una
gráfica el cambio de
presión P como una función de la distancia x. La
distancia entre dos compresiones o rarefacciones sucesivas es la
longitud de onda.
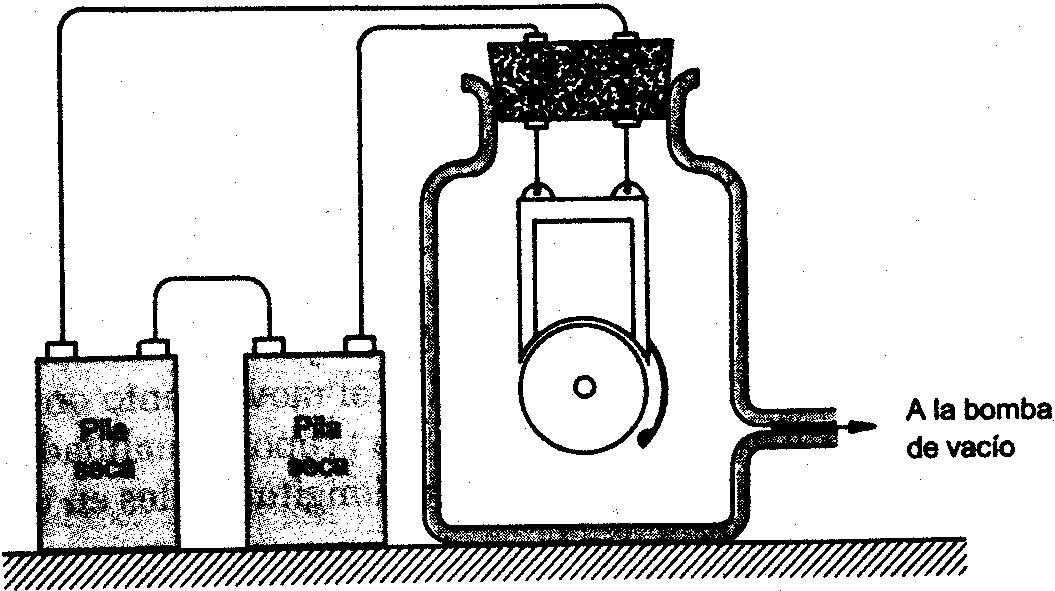
Un timbre que se acciona en el vacío no puede
escucharse. Es necesario un medio material para que se produzca
sonido.
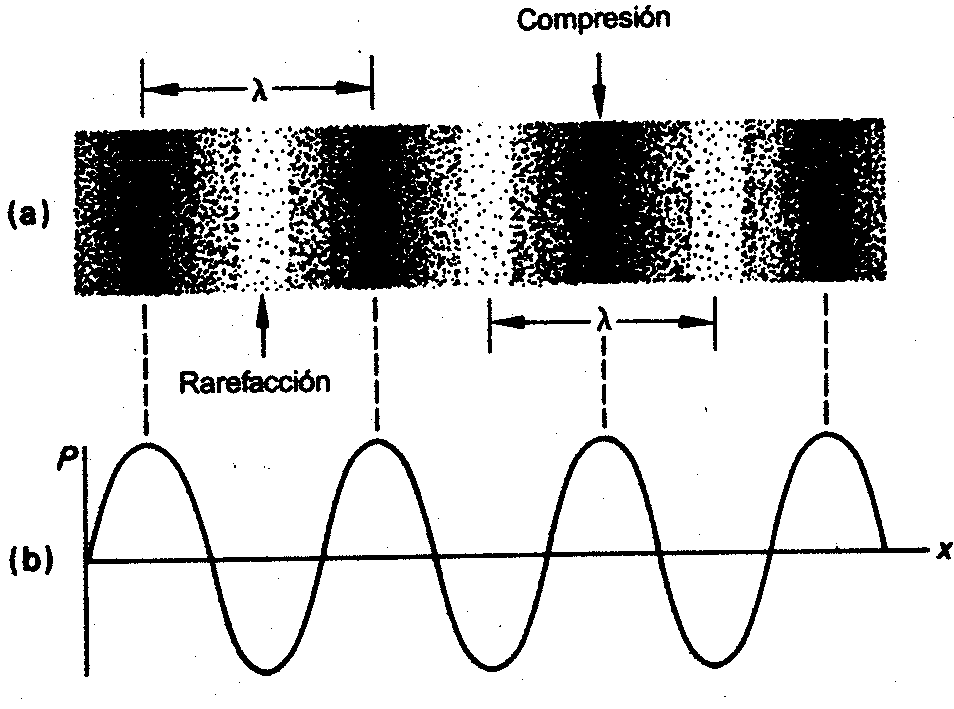
(a) Compresiones y rarefacciones de una onda sonora en
el aire en un instante determinado. (b) Variación
sinusoidal de la presión como función del
desplazamiento.
Cualquier persona que haya
visto a cierta distancia cómo se dispara un proyectil ha
observado el fogonazo del arma antes de escuchar la
detonación. Ocurre algo similar al observar el
relámpago de un rayo antes de oír el trueno. Aunque
tanto la luz como el
sonido viajan a velocidades finitas, la velocidad de la luz es
tan grande en comparación con la del sonido que pueden
considerarse instantánea. La velocidad del sonido se puede
medir directamente determinando el tiempo que tardan
las ondas en moverse a través de una distancia conocida.
En el aire, a 0ºC, el sonido viaja a una velocidad de 331
m/s (1087 ft/s).
La velocidad de una onda depende de la elasticidad del
medio y de la inercia de sus partículas. Los materiales
más elásticos permiten mayores velocidades de onda,
mientras que los materiales más densos retardan el
movimiento ondulatoria. Las siguientes relaciones
empíricas se basan en estas proporcionalidades.
Para las ondas sonoras longitudinales en un alambre o
varilla, la velocidad de onda está dada por

donde Y es el módulo de Young para el
sólido y p es su densidad. Esta
relación es válida sólo para varillas cuyos
diámetros son pequeños en comparación con
las longitudes de las ondas sonoras longitudinales que se
propagan a través de ellas.
En un sólido extendido, la velocidad de la onda
longitudinal es función del módulo de corte S, el
módulo de volumen B, y la
intensidad p del medio. La velocidad de la onda se puede calcular
a partir de
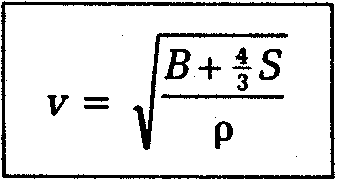
Las ondas longitudinales transmitidas en un fluido
tienen una velocidad que se determina a partir de

donde B es módulo de volumen para
el fluido y p es su densidad.
Para calcular la velocidad del sonido en un gas, el
módulo de volumen está dado por
![]()
donde y es la constante adiabática (y = 1.4 para
el aire y los gases
diatómicos) y P es la presión del gas. Por lo
tanto, la velocidad de las ondas longitudinales en un gas,
partiendo de la ecuación del fluido, está dada
por
![]()
Pero para un gas ideal

Donde R = constante universal de los gases
T = temperatura
absoluta del gas
M = masa molecular del gas
Sustituyendo la ecuación nos queda

Ejemplos.


4.
Vibración Forzada y Resonancia.
Cuando un cuerpo que está vibrando se pone en
contacto con otro, el segundo cuerpo se ve forzado a vibrar con
la misma frecuencia que el original. Por ejemplo, si un
diapasón es golpeado con un martillo y luego se coloca su
base contra la cubierta de una mesa de madera, la
intensidad del sonido se incrementará repentinamente.
Cuando se separa de la mesa el diapasón, la intensidad
disminuye a su nivel original. Las vibraciones de las
partículas de la mesa en contacto con el diapasón
se llaman vibraciones forzadas.
Hemos visto que los cuerpos elásticos tienen
ciertas frecuencias naturales de vibración que son
características del material y de las
condiciones límite (de frontera). Una cuerda tensa de una
longitud definida puede producir sonidos de frecuencias
características. Un tubo abierto o cerrado también
tiene frecuencias naturales de vibración. Siempre que se
aplican a un cuerpo una serie de impulsos periódicos de
una frecuencia casi igual a alguna de las frecuencias naturales
del cuerpo, éste se pone a vibrar con una amplitud
relativamente grande. Este fenómeno se conoce como
resonancia o vibración simpática.
Un ejemplo de resonancia es el caso de un niño
sentado a un columpio. La experiencia indica que la
oscilación puede ser puesta en vibración con gran
amplitud por medio de una serie de pequeños empujones
aplicados a intervalos regulares. La resonancia se
producirá únicamente cuando los empujones
estén en fase con la frecuencia natural de
vibración del columpio. Una ligera variación de los
pulsos de entrada dará como resultado una vibración
pequeña o incluso ninguna.
El refuerzo del sonido por medio de la resonancia tiene
múltiples aplicaciones, así como también
buen número de consecuencias desagradables. La resonancia
en una columna de aire en un tubo de órgano amplifica el
débil sonido de una vibración de un chorro de aire
vibrante. Muchos instrumentos
musicales se diseñan con cavidades resonantes para
producir una variedad de sonidos. La resonancia eléctrica
en los receptores de radio permite al
oyente percibir con claridad las señales débiles.
Cuando se sintoniza la frecuencia de la estación elegida,
la señal se amplifica por resonancia eléctrica. En
auditorios mal diseñados o enormes salas de concierto, la
música y
las voces pueden tener un sonido profundo que resulta
desagradable al oído. Se sabe que los puentes se destruyen
debido a vibraciones simpáticas de gran amplitud
producidas por ráfagas de viento.
Hemos definido el sonido como una onda mecánica
longitudinal que se propaga a través de un medio
elástico. Éste es una definición amplia que
no impone restricciones a ninguna frecuencia del sonido. Los
fisiólogos se interesan principalmente en las ondas
sonoras que son capaces de afectar el sentido del oído.
Por lo tanto, es conveniente dividir el espectro del sonido de
acuerdo con las siguientes definiciones.
Sonido audible es el que corresponde a las ondas sonoras
en un intervalo de frecuencias de 20 a 20 000 Hz.
Las ondas sonoras que tienen frecuencias por debajo del
intervalo audible se denominan infrasónicas.
Las ondas sonoras que tienen frecuencias por encima del
intervalo audible se llaman ultrasónicas.
Cuando se estudian los sonidos audibles, los
fisiólogos usan los términos, fuerza, tono y
calidad
(timbre) p’ara describir las sensaciones producidas. Por
desgracia, estos términos representan magnitudes
sensoriales y por lo tanto subjetivas. Lo que es volumen fuerte
para una persona es moderado para otra. Lo que alguien percibe
como calidad, otro lo considera inferior. Como siempre, los
físicos deben trabajar con definiciones explícitas
medibles. Por lo tanto, el físico intenta correlacionar
los efectos sensoriales con las propiedades físicas de las
ondas. Estas correlaciones se resumen en la siguiente
forma:
Efectos sensoriales Propiedad
física
Intensidad acústica (Volumen)
Intensidad
Tono Frecuencia
Timbre (Calidad) Forma de la onda
El significado de los términos de la izquierda
puede variar considerablemente de uno a otro individuo. Los
términos de la derecha son medibles y objetivos.
Las ondas sonoras constituyen un flujo de energía
a través de la materia. La intensidad de una onda sonora
específica es una medida de la razón a la cual la
energía se propaga a través de un cierto volumen
espacial. Un método
conveniente para especificar la intensidad sonora es en
términos de la rapidez con que la energía se
transfiere a través de la unidad de área normal a
la dirección de la propagación de la onda. Puesto
que la rapidez a la cual fluye la energía es la potencia de una
onda, la intensidad puede relacionarse con la potencia por unidad
de área que pasa por un punto dado.
La intensidad sonora es la potencia transferida por una
onda sonora a través de la unidad de área normal a
la dirección de la propagación.
![]()

La intensidad de una onda sonora es una medida de la
potencia transmitida por unidad de área perpendicular a la
dirección de propagación de onda.
Las unidades para la intensidad resultan de la
relación de una unidad de potencia entre una unidad de
área. En unidades del SI, la intensidad se expresa en
W/m2, y ésa es la unidad que emplearemos. Sin
embargo, la rapidez de flujo de energía en ondas sonoras
es pequeña, y en la industria se
usa todavía ?W/cm2 en múltiples
aplicaciones. El factor de conversión es:
1 ?W/cm2 = 1 x 10-2
W/m2
Se puede demostrar por métodos
similares a los utilizados para un resorte que está
vibrando, que la intensidad sonora varía en forma directa
al cuadrado de la frecuencia f y al cuadrado de la amplitud A de
una determinada onda sonora. Simbólicamente, la intensidad
I esta dada por:
I = 2?2f
2A2pv
Donde v es la velocidad del sonido en un medio de
densidad p. El símbolo A en la ecuación se refiere
a la amplitud de la onda sonora y no a la unidad de
área.
La intensidad I0 del sonido audible apenas
perceptible es el orden de 10-12 W/m2 .
Esta intensidad, que se conoce como umbral de audición, ha
sido adoptado por expertos en acústica como la intensidad
mínima para que un sonido sea audible.
El umbral de audición representa el patrón
de la intensidad mínima para que un sonido sea audible. Su
valor a una
frecuencia de 1000 Hz es:
I0 = 1 x 10-2
W/m2 = 1 x 10-10
?W/cm2
El intervalo de intensidades por arriba del cual el
oído humano es sensible es enorme. Abarca desde el umbral
de audición I0 hasta una intensidad de
10-12 veces mayor. EL extremo superior representa el
punto en el que la intensidad es intolerable para el oído
humano. La sensación se vuelve dolorosa y no sólo
auditiva.
El umbral del dolor representa la intensidad
máxima que el oído promedio puede registrar sin
sentir dolor. Su valor es:
1p = 1 W/m2 = 100
?W/cm2
En vista de la amplitud del intervalo de intensidades al
que es sensible el oído, es más conveniente
establecer una escala
logarítmica para las mediciones de intensidades sonoras.
Dicha escala se establece a partir de la siguiente
regla.
Cuando la intensidad I, de un sonido es 10 veces mayor
que la intensidad I2 de otro, se dice que la
relación de intensidades es de 1 bel (B).
O sea que, cuando se compara la intensidad de dos
sonidos, nos referimos a la diferencia entre niveles de
intensidad dada por:
![]()
donde I, es la unidad de un sonido e I2 es la
intensidad del otro.
Ejemplos
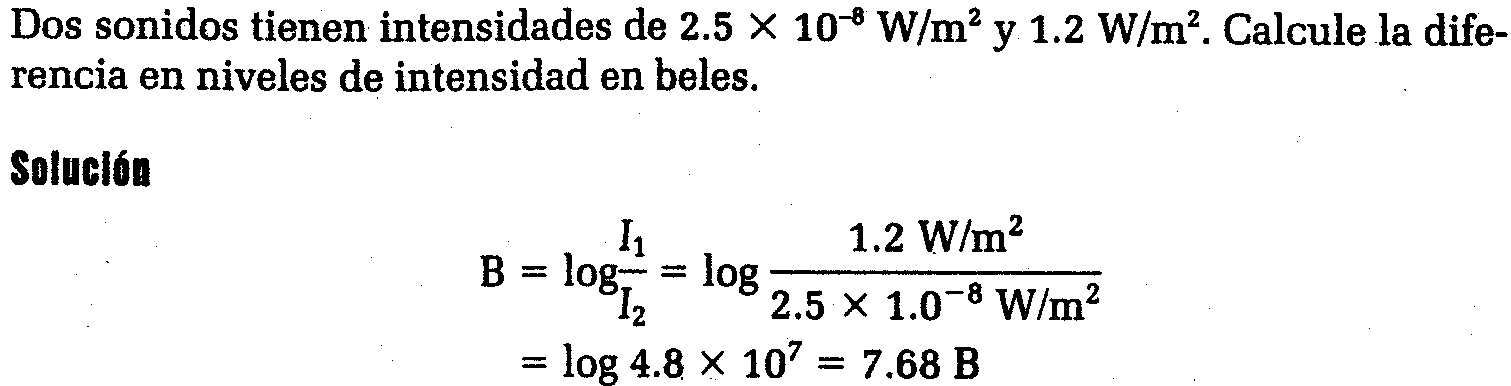
En la práctica, la unidad de 1 B es demasiado
grande. Para obtener una unidad más util, se define el
decibel (dB) como un décimo del bel. Por lo tanto, la
respuesta al ejemplo también se puede expresar como 76.8
dB.
Usando la intensidad I0 como patrón de
comparación para todas las intensidades, es posible
establecer una escala general para valorar cualquier sonido. El
nivel de intensidad en decibeles de cualquier sonido de
intensidad I puede calcularse a partir de la relación
general.
![]()
donde I0 es la intensidad del umbral de
audición (1 x 10-12 W/m2). El nivel
de intensidad para I0 es de cero decibeles.

En virtud de la notación logarítmica de
los decibeles, el amplio intervalo de intensidades a niveles de
intensidad se reduce a un espectro de 0 a 120 dB. Debemos
recordar, sin embargo, que la escala no es lineal sino
logarítmica. Un sonido de 40 dB es mucho más que el
doble de intensidad de un sonido de 20 dB. Un sonido es 100 veces
más intenso que otro es tan sólo 20 dB mayor. En la
tabla aparecen varios ejemplos de los niveles de intensidad de
sonidos comunes.
El efecto de la intensidad en el oído humano se
manifiesta en sí mismo como volumen. En general, las ondas
sonoras que son más intensas son también de mayor
volumen, pero el oído no es igualmente sensible a sonidos
de todas las frecuencias. Por lo tanto, un sonido de alta
frecuencia puede ni parecer tan alto como uno de menor frecuencia
que tenga la misma intensidad.
La frecuencia de un sonido determina lo que el
oído juzga como el tono del sonido. Los músicos
designan el tono por las letras que corresponden a las notas de
las teclas del piano. Por ejemplo, las notas do, re y fa se
refieren a tonos específicos, o frecuencias. Un disco de
sirena, como el que se muestra en la
figura, puede utilizarse para demostrar cómo el tono queda
determinado por la frecuencia de un sonido. Una corriente de aire
se envía sobre una hilera de agujeros igualmente
espaciados. Al variar la velocidad de rotación del disco,
el tono del sonido resultante se incrementa o decrece.
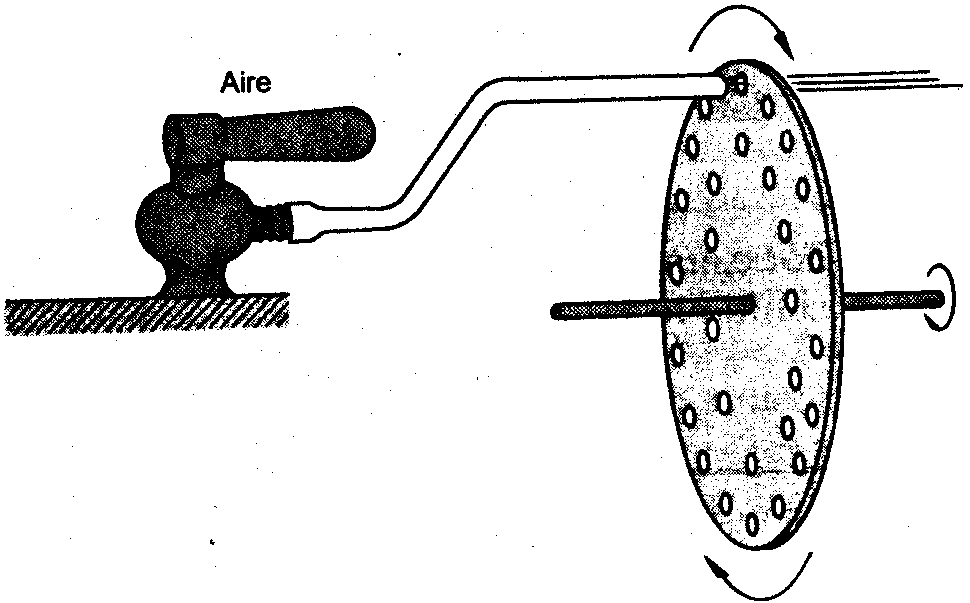
Demostración de la relación
entre tono y frecuencia.
Dos sonidos del mismo tono se pueden distinguir
fácilmente. Por ejemplo, suponga que suena la nota do (250
Hz) sucesivamente en un piano, una flauta, una trompeta y un
violín. Aun cuando cada sonido tiene el mismo tono, hay
una marcada diferencia en el timbre. Se dice que esta diferencia
resulta una diferencia en la calidad o timbre del
sonido.
En los instrumentos musicales, independientemente de la
fuente de vibración, generalmente se excitan en forma
simultánea diversos modos de oscilación. Por
consiguiente, el sonido producido consiste no sólo en la
fundamental, sino también en varios sobretonos. La calidad
de un sonido se determina por el número y las intensidades
relativas de los sobretonos presentes. La diferencia en la
calidad o timbre entre dos sonidos puede observarse en forma
objetiva analizando las complejas formas de onda que resultan de
cada sonido. En general, cuanto más compleja es la onda,
mayor es el número de armónicas que contribuyen a
dicha complejidad.
7. Interferencia y
pulsaciones.
La interferencia también se presenta en el caso
de las ondas sonoras longitudinales y el principio de
superposición también se les aplica a ellas. Un
ejemplo común de la interferencia en ondas sonoras se
presenta cuando dos diapasones (o cualquier otra fuente sonora de
una sola frecuencia) cuyas frecuencias difieren ligeramente, se
golpean de manera simultánea. El sonido que se produce
varía en intensidad, alternando entre tonos fuertes y
silencio virtual. Estas pulsaciones regulares se conocen como
pulsaciones. El efecto vibrato que se obtiene en algunos
órganos es producida por dos tubos sintonizados a
frecuencias ligeramente diferentes.
Para comprender el origen de las pulsaciones, examinemos
la interferencia que se establece entre ondas sonoras que
producen de dos diapasones de frecuencia ligeramente distinta. La
superposición de ondas A y B ilustran el origen de las
pulsaciones. Los tonos fuertes se presentan cuando las ondas
interfieren constructivamente y los tonos suaves ocurren cuando
las ondas interfieren en forma destructiva. La observación y los cálculos
demuestran que las dos ondas interfieren constructivamente f
– f’ veces por segundo. Así podemos
escribir
Número de pulsaciones por segundo
= |f – f’|
Por ejemplo si dos diapasones de 256 y 259 Hz se golpean
simultáneamente, el sonido resultante pulsará tres
veces por segundo.
Siempre que una fuente sonora se mueve en
relación con un oyente, el tono del sonido, como lo
escucha el observador, puede no ser el mismo que el que percibe
cuando la fuente está en reposo. Por ejemplo, si uno
está cerca de la vía del ferrocarril y escucha el
silbato del tren al aproximarse, se advierte que el tono del
silbido es más alto que el normal que se escucha cuando el
tren está detenido. A medida que el tren se aleja, se
observa que el tono que se escucha es más bajo que el
normal. En forma similar, en las pistas de carreras, el sonido de
los automóviles que se acercan a la gradería es
considerablemente más alto en tono que el sonido de los
autos que se
alejan de la gradería.
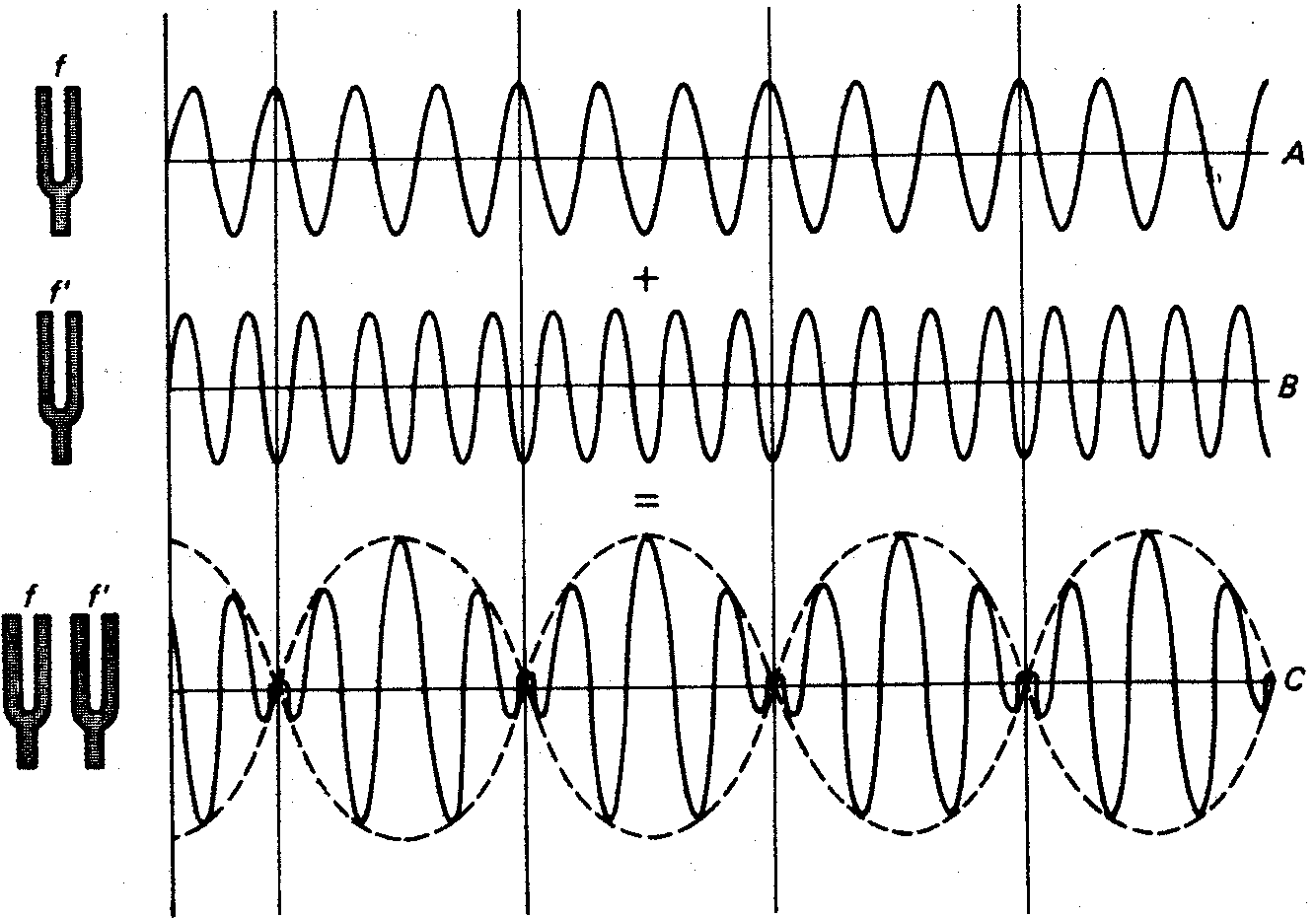
Diagrama que muestra el origen de las pulsaciones. La
onda C es una superposición de ondas A y B.
El fenómeno no se restringe al movimiento de la
fuente. Si la fuente de sonido está fija, un oyente que se
mueva hacia la fuente observará un aumento similar en el
tono. Un oyente que se aleja de la fuente de sonido
escuchará un sonido de menor tono. El cambio en la
frecuencia del sonido que resulta del movimiento relativo entre
una fuente y un oyente se denomina efecto Doppler.
El efecto Doppler se refiere al cambio aparente en la
frecuencia de una fuente de sonido cuando hay un movimiento
relativo de la fuente y del oyente.
El origen del efecto Doppler se puede demostrar
gráficamente por medio de la representación de las
ondas periódicas emitidas por una fuente como
círculos concéntricos que se mueven en forma radial
hacia fuera. La distancia entre cualquier par de círculos
representa la longitud de onda ??del sonido que se desplaza con
una velocidad V. La frecuencia con que estas ondas golpean el
oído determina el tono de sonido escuchado.
Consideremos en primer lugar que la fuente se mueve a la
derecha hacia un observador A inmóvil. A medida que la
fuente en movimiento emite ondas sonoras, tiende a alcanzar las
ondas que viajan en la misma dirección que ella. Cada onda
sucesiva se emite desde un punto más cercano al oyente que
la onda inmediata anterior. Esto da por resultado que la
distancia entre las ondas sucesivas, o la longitud de onda, sea
menor que la normal. Una longitud de onda más
pequeña producen una frecuencia de ondas mayor, lo que
aumenta el tono del sonido escuchado por el oyente A. Mediante un
razonamiento similar se demuestra que un incremento en la
longitud de las ondas que llegan al oyente B hará que B
escuche un sonido de menor frecuencia.
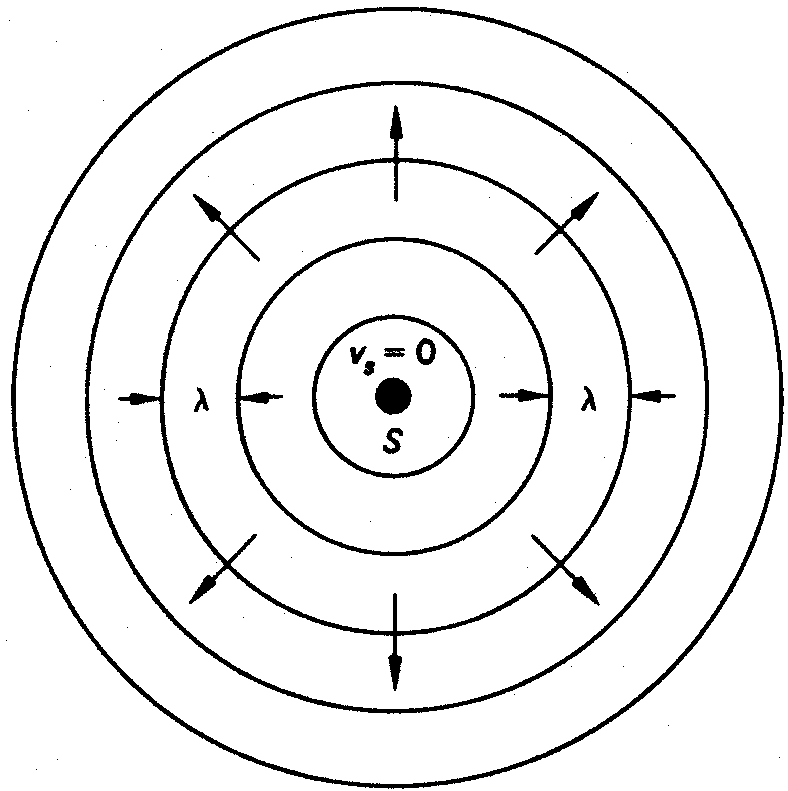
Representación gráfica de
ondas sonoras emitidas desde una fuente fija.
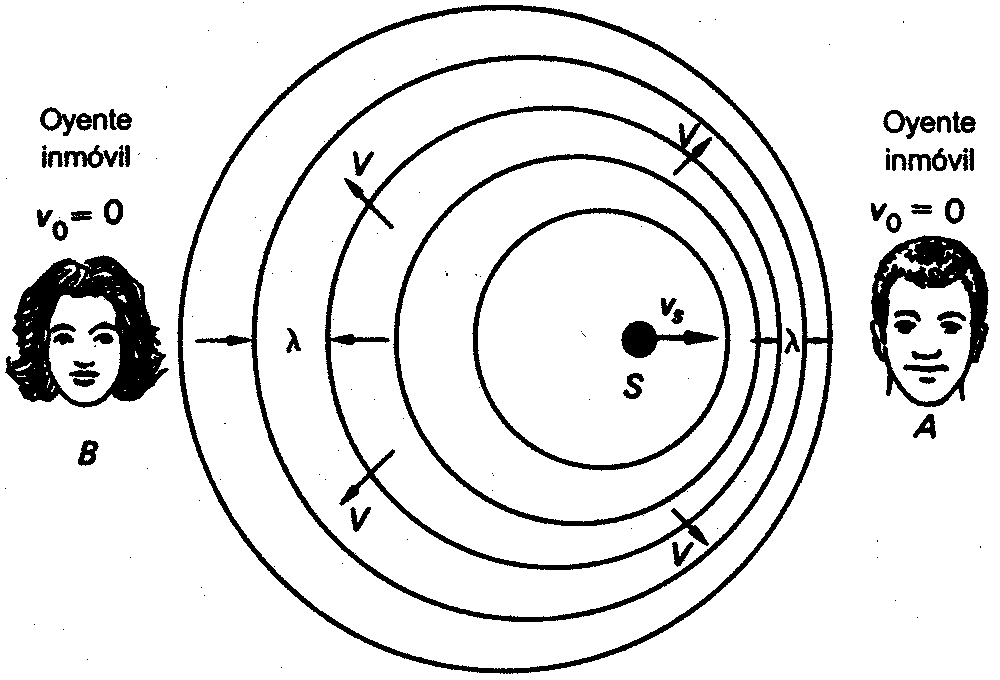
Ilustración del efecto Doppler. Las ondas frente
a una fuente en movimiento están más cercanas entre
sí que las ondas que se propagan detrás de la
fuente móvil.
Ahora podemos deducir una relación para predecir
el cambio en la frecuencia observada. Durante una
vibración completa de la fuente estacionaria (un tiempo
igual al del periodo T),cada onda se moverá a lo largo de
una distancia de una longitud de onda. Esta distancia de una
longitud de onda. Esta distancia se presenta con ??y está
dada por:
![]()

Cálculo de la magnitud de la longitud de onda del
sonido que se emite desde una fuente en movimiento. La velocidad
de la fuente Vs se considera positiva para velocidades
de acercamiento y negativa para velocidades de
alejamiento.
Donde V es la velocidad de sonido y fs es la
frecuencia de la fuente. Si la fuente se mueve a la derecha con
una velocidad Vs , la nueva longitud de onda ?’
al frente de la fuente será:
?’ = VT – VsT = (V –
Vs) T
Esta ecuación también se aplica para la
longitud de onda a la izquierda de la fuente en movimiento si
seguimos la convención de que las velocidades al
aproximarse se consideran positivas, y las velocidades al
alejarse se consideran negativas. Por lo tanto, si calculamos
?’ a la izquierda de la fuente en movimiento, el valor
negativo sería sustituido para Vs’ dando
por resultado una mayor longitud de onda.
La velocidad del sonido en un medio es función de
las propiedades del medio y no depende del movimiento de la
fuente. Así, la frecuencia f0 escuchada por un
oyente inmóvil y proveniente de una fuente en movimiento
de frecuencia fs’ está dada
por:
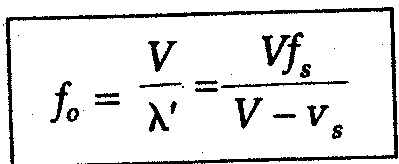
donde V es la velocidad del sonido y Vs es la
velocidad de la fuente. La velocidad Vs se considera
como positiva para velocidades de acercamiento y negativa para
velocidades de alejamiento.
Trabajo enviado y realizado por:
Leopoldo de la Fuente Silva
Estudiante del Instituto Tecnológico de Cd.
Victoria