Teoría
El plano cartesiano:
EL PLANO CARTESIANO.
El plano cartesiano está formado por dos rectas
numéricas, una horizontal y otra vertical que se cortan en
un punto. La recta horizontal es llamada eje de las abscisas o de
las equis (x), y la vertical, eje de las ordenadas o de las yes,
(y); el punto donde se cortan recibe el nombre de origen.
El plano cartesiano tiene como finalidad describir la
posición de puntos, los cuales se representan por sus
coordenadas o pares ordenados. Las coordenadas se forman
asociando un valor del eje
de las "X" y uno de las "Y", respectivamente, esto indica que un
punto se puede ubicar en el plano cartesiano con base en sus
coordenadas, lo cual se representa como:
P (x,
y)

Para localizar puntos en el plano cartesiano se debe
llevar a cabo el siguiente procedimiento:
1. Para localizar la abscisa o valor de x, se cuentan
las unidades correspondientes hacia la derecha si son positivas o
hacia a izquierda si son negativas, a partir del punto de origen,
en este caso el cero.
2. Desde donde se localiza el valor de x, se cuentan
las unidades correspondientes hacia arriba si son positivas o
hacia abajo, si son negativas y de esta forma se localiza
cualquier punto dadas sus coordenadas.

Ejemplos:
Localizar el punto A ( -4, 5 ) en el plano cartesiano. Este
procedimiento también se emplea cuando se requiere
determinar las coordenadas de cualquier punto que esté en
el plano cartesiano.
Determinar las coordenadas del punto M.
Las coordenadas del punto M son (3,-5).

De lo anterior se concluye que:
Para determinar las coordenadas de un punto o localizarlo en
el plano cartesiano, se encuentran unidades correspondientes en
el eje de las x hacia la derecha o hacia la izquierda y luego las
unidades del eje de las y hacia arriba o hacia abajo,
según sean positivas o negativas, respectivamente.
Doña Lupe nos ha dicho que su
farmacia está dentro del centro de la ciudad .
Supongamos que deseamos saber la ubicación exacta de
la farmacia de Doña Lupe Una vez que ya
estamos en el centro le preguntamos a un
policía para que nos oriente. El policía nos ha
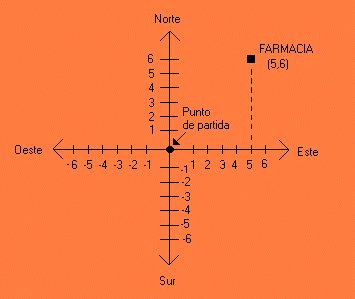
dicho que caminemos 5 cuadras hacía el este y 6 cuadras
hacía el norte para llegar a la farmacia.La cantidad de
cuadras que tenemos que caminar las podemos entender como
coordenadas en un plano cartesiano.
Lo anterior lo podemos expresar en un plano cartesiano de la
siguiente manera:
Para el problema planteado , el origen del plano será
el punto de partida que es en donde le preguntamos al
policía sobre la ubicación de la farmacia.
Funciones lineales:
Esta clase de
funciones
tienen dos características esenciales:
- Las variaciones entre dos valores de
la variable independiente y la de sus correspondientes de
la variable dependiente son uniformes. - Todos los puntos de su gráfica están
alineados.
Funciones de proporcionalidad directa:
Si en todos los pares de valores de una función de
proporcionalidad directa dividimos la ordenada por la abscisa,
obtenemos siempre el mismo número. Ese valor se llama
constante de proporcionalidad, y se escribe habitualmente
k.
Funciones de proporcionalidad inversa:
Si en todos los pares de valores de una función de
proporcionalidad inversa multiplicamos la ordenada por la
abscisa, obtenemos siempre el mismo número, que es la
constante de proporcionalidad, y habitualmente se escribe
k.
Propuestas de
Actividades
Pág. 41
Act. 37
Ignacio participa en el triatlón de su ciudad, que
consiste en tres trayectos: el primero es de carrera pedestre, el
segundo es de nado en una laguna y el último es de
mountain-bike.
Observen la gráfica, que muestra la altura
con respecto al nivel de la laguna que se encuentra Ignacio en
cada momento de la competencia, y
respondan a las preguntas.
a) ¿Cuánto
tiempo
tardó en alcanzar la altura máxima?
Página siguiente  |
