Coeficiente de correlación de Karl Pearson –
Monografias.com
Coeficiente de correlación de
Karl Pearson
Dado dos variables, la correlación permite hacer
estimaciones del valor de una de ellas conociendo el valor de la
otra variable.
Los coeficientes de correlación son medidas que
indican la situación relativa de los mismos sucesos
respecto a las dos variables, es decir, son la expresión
numérica que nos indica el grado de relación
existente entre las 2 variables y en qué medida se
relacionan. Son números que varían entre los
límites +1 y -1. Su magnitud indica el grado de
asociación entre las variables; el valor r = 0 indica que
no existe relación entre las variables; los valores ( 1
son indicadores de una correlación perfecta positiva (al
crecer o decrecer X, crece o decrece Y) o negativa (Al crecer o
decrecer X, decrece o crece Y).
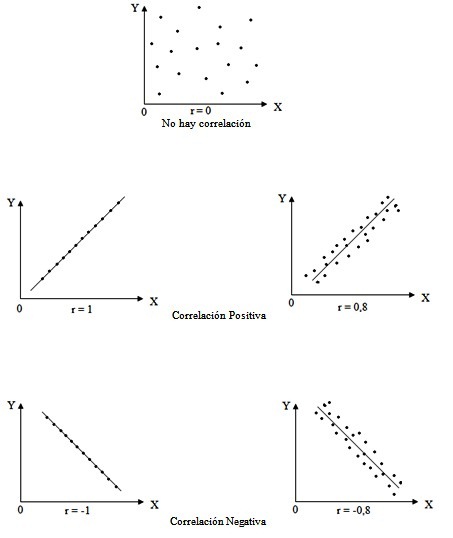
Para interpretar el coeficiente de correlación
utilizamos la siguiente escala:
Valor | Significado | ||
-1 | Correlación negativa grande y | ||
-0,9 a -0,99 | Correlación negativa muy alta | ||
-0,7 a -0,89 | Correlación negativa alta | ||
-0,4 a -0,69 | Correlación negativa moderada | ||
-0,2 a -0,39 | Correlación negativa baja | ||
-0,01 a -0,19 | Correlación negativa muy baja | ||
0 | Correlación nula | ||
0,01 a 0,19 | Correlación positiva muy baja | ||
0,2 a 0,39 | Correlación positiva baja | ||
0,4 a 0,69 | Correlación positiva moderada | ||
0,7 a 0,89 | Correlación positiva alta | ||
0,9 a 0,99 | Correlación positiva muy alta | ||
1 | Correlación positiva grande y | ||
a) Para datos no agrupados se calcula aplicando la
siguiente ecuación:

Ejemplo ilustrativo:
Con los datos sobre las temperaturas en dos días
diferentes en una ciudad, determinar el tipo de
correlación que existe entre ellas mediante el coeficiente
de PEARSON.
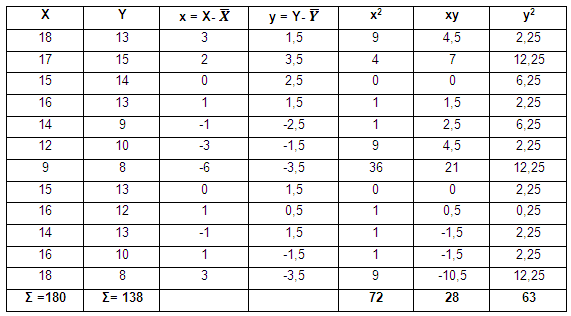
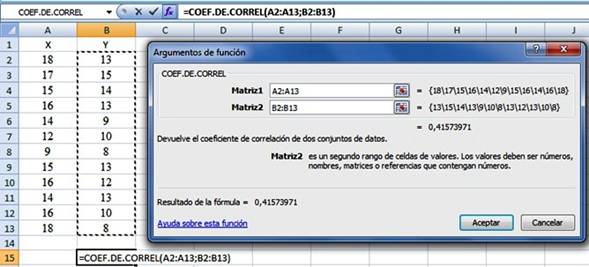
X | 18 | 17 | 15 | 16 | 14 | 12 | 9 | 15 | 16 | 14 | 16 | 18 | SX =180 | ||
Y | 13 | 15 | 14 | 13 | 9 | 10 | 8 | 13 | 12 | 13 | 10 | 8 | SY= 138 | ||
Solución:
Se calcula la media aritmética
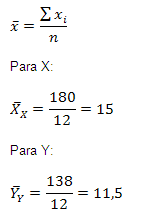
Se llena la siguiente tabla:
Se aplica la fórmula:
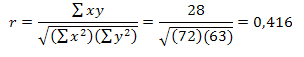
Existe una correlación moderada
En Excel se calcula de la siguiente
manera:
a) Se inserta la función COEF.DE.CORREL y pulsar
en Aceptar. En el cuadro de argumentos de la función, en
el recuadro de la Matriz 1 seleccionar las celdas de X, y en el
recuadro de la Matriz 2 seleccionar las celdas de Y. Pulsar en
Aceptar.
b) Para datos agrupados, el coeficiente de
Correlación de Pearson se calcula aplicando la siguiente
fórmula:
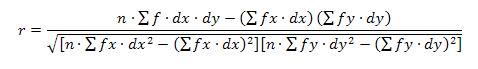
Donde
n = número de datos.
f = frecuencia de celda.
fx = frecuencia de la variable X.
fy = frecuencia de la variable Y.
dx = valores codificados o cambiados para los intervalos
de la variable X, procurando que al intervalo central le
corresponda dx = 0, para que se hagan más fáciles
los cálculos.
dy = valores codificados o cambiados para los intervalos
de la variable X, procurando que al intervalo central le
corresponda dy = 0, para que se hagan más fáciles
los cálculos.
Ejemplo ilustrativo:
Con los siguientes datos sobre los Coeficientes
Intelectuales (X) y de las calificaciones en una prueba de
conocimiento (Y) de 50 estudiantes:
N° de estudiante | X | Y | N° de estudiante | X | Y | ||
1 | 76 | 28 | 26 | 88 | 40 | ||
2 | 77 | 24 | 27 | 88 | 31 | ||
3 | 78 | 18 | 28 | 88 | 35 | ||
4 | 79 | 41 | 29 | 88 | 26 | ||
5 | 79 | 43 | 30 | 89 | 30 | ||
6 | 80 | 45 | 31 | 89 | 24 | ||
7 | 80 | 34 | 32 | 90 | 18 | ||
8 | 81 | 18 | 33 | 90 | 11 | ||
9 | 82 | 40 | 34 | 90 | 15 | ||
10 | 82 | 35 | 35 | 91 | 38 | ||
11 | 83 | 30 | 36 | 92 | 34 | ||
12 | 83 | 21 | 37 | 92 | 31 | ||
13 | 83 | 22 | 38 | 93 | 33 | ||
14 | 83 | 23 | 39 | 93 | 35 | ||
15 | 84 | 25 | 40 | 93 | 24 | ||
16 | 84 | 11 | 41 | 94 | 40 | ||
17 | 84 | 15 | 42 | 96 | 35 | ||
18 | 85 | 31 | 43 | 97 | 36 | ||
19 | 85 | 35 | 44 | 98 | 40 | ||
20 | 86 | 26 | 45 | 99 | 33 | ||
21 | 86 | 30 | 46 | 100 | 51 | ||
22 | 86 | 24 | 47 | 101 | 54 | ||
23 | 86 | 16 | 48 | 101 | 55 | ||
24 | 87 | 20 | 49 | 102 | 41 | ||
25 | 88 | 36 | 50 | 102 | 45 | ||
1) Elaborar una tabla de dos variables
2) Calcular el coeficiente de
correlación
Solución:
1) En la tabla de frecuencias de dos variables,
cada recuadro de esta tabla se llama una celda y
corresponde a un par de intervalos, y el número indicado
en cada celda se llama frecuencia de celda. Todos los
totales indicados en la última fila y en la última
columna se llaman totales marginales o frecuencias
marginales, y corresponden, respectivamente, a las
frecuencias de intervalo de las distribuciones de frecuencia
separadas de la variable X y Y.
Para elaborar la tabla se recomienda:
– Agrupar las variables X y Y en un igual número
de intervalos.
– Los intervalos de la variable X se ubican en la parte
superior de manera horizontal (fila) y en orden
ascendente.
– Los intervalos de la variable Y se ubican en la parte
izquierda de manera vertical (columna) y en orden
descendente.
Para elaborar los intervalos se procede a realizar los
cálculos respectivos:
En la variable X:

En la variable Y:

Nota: Para la variable X se tomará un
ancho de intervalo igual a 5 y para la variable Y un ancho de
intervalo igual a 8 para obtener un número de intervalos
igual a 6 para cada variable.
Contando las frecuencias de celda para cada par de
intervalos de las variables X y Y se obtiene la siguiente tabla
de frecuencias de dos variables:

Interpretación:
– El número 5 es la frecuencia de la celda
correspondiente al par de intervalos 86-90 en Coeficiente
Intelectual y 19-26 en Calificación obtenida en la prueba
de conocimiento.
– El número 8 en la fila de fx es el total
marginal o frecuencia marginal del intervalo 76-80 en Coeficiente
Intelectual.
– El número 14 en la columna de fy es el total
marginal o frecuencia marginal del intervalo 35-42 en
Calificación obtenida en la prueba de
conocimiento.
– El número 50 es total de frecuencias marginales
y representa al número total de estudiantes.
2) Realizando los cálculos respectivos se obtiene
la siguiente tabla:

Nota:
Los números de las esquinas de cada celda en la
anterior tabla representan el producto f·dx·dy,
así por ejemplo, para obtener el número el
número -8 de los intervalos 76-80 en X y 43-50 en Y se
obtiene multiplicando 2·(-2)·(2) = -8. Para obtener
el número 6 de los intervalos 96-100 en X y 51-58 en Y se
obtiene multiplicando 1·2·3 = 6.
Los números de la última columna (24, -2,
7, 0, 5 y 12) se obtienen sumando los números de las
esquinas en cada fila, así por ejemplo, para obtener el
número 24 se suma 6 + 18 = 24.
Los números de la última fila (0, 5, 0, 2,
12 y 27) se obtienen sumando los números de las esquinas
en cada columna, así por ejemplo, para obtener el
número 27 se suma 18 + 6 + 3 = 27.

Para obtener último número de la
última fila se obtiene sumando los resultados de la
última fila (46=0+5+0+2+12+27), y tiene que ser igual al
último número de la última columna como
comprobación que los cálculos de la tabla han sido
correctos.
Observando los datos en la tabla anterior se reemplaza
los valores en la ecuación del Coeficiente de
Correlación de Pearson para datos agrupados se
obtiene:

Existe una correlación positiva
moderada
REFERENCIAS
BIBLIOGRÁFICAS
BENALCÁZAR, Marco, (2002), Unidades para Producir
Medios Instruccionales en Educación, SUÁREZ, Mario
Ed. Graficolor, Ibarra, Ecuador.
DAZA, Jorge, (2006), Estadística Aplicada con
Microsoft Excel, Grupo Editorial Megabyte, Lima,
Perú.
GOVINDEN, Lincoyán, (1985), Introducción a
la Estadística, Ed. McGraw Hill. Interamericana
Editores. S.A., Bogotá, Colombia.
JOHNSON, Robert, (2003), Estadística
Elemental, Ed. Math Learning, Ed. Tercera, México
DF.
KUBY, Patricia.
KAZMIER, J. Leonard, (1990).
Estadística Aplicada a la Administración y la
Economía, Ed. McGrawHill, Ed. Segunda,
Bogotá, Colombia.
LIND, Marchal, (2005), Estadística Aplicada a los
Negocios y a la Economía, Ed. McGraw- Hill,
MASON Ed. Décima., Mexico DF.
MARTINEZ, Bencardino, (1981), Estadística
Comercial, Ed. Norma, Bogotá, Colombia.
MORENO, Francis, (1993), Estadística Inferencial,
Universidad Particular de Loja, Loja, Ecuador.
SÁNCHEZ, Jesús, (2007),
Introducción a la Estadística Empresarial, Madrid,
España.
SALTOS, Héctor, (1986), Estadística de
Inferencia, Ed. Pío XII, Ambato, Ecuador.
SHAO, Stephen, (1980), Estadística para
Economistas y Administradores de Empresas, Ed. Herrero
Hnos, México DF.
SPIEGEL, Murray, (2000),
Estadística, Serie de Compendios Schaum, Ed. McGraw-Hill,
México.
SUÁREZ, Mario, (2004), Interaprendizaje
Holístico de Matemática, Ed. Gráficas
Planeta, Ibarra, Ecuador.
STEVENSON, William, (1981), Estadística para
Administración y Economía, Ed. Harla S.A de
C.V. México D.F.
WEBSTER, Allen, (2000), Estadística Aplicada a
los Negocios y a la Economía, Ed. McGraw Hill.
Interamericana Editores S.A. Bogotá,
Colombia
Autor:
Mario Orlando Suárez
Ibujes