11 EJERCICIO 26 : Formula y plantea mediante programación
lineal el siguiente caso de una oficina de correos que desea
minimizar el número de empleados de tiempo completo que
hay que contratar sabiendo que necesita un número
diferente de empleados a tiempo completo, para cada día de
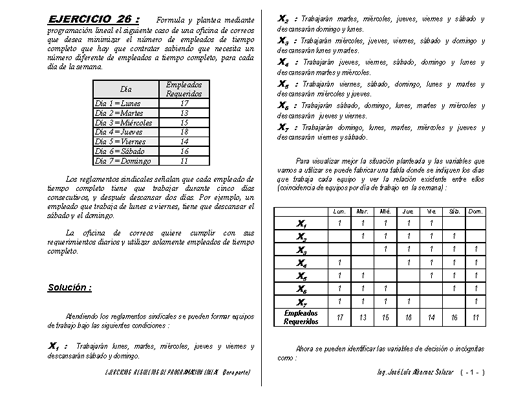
la semana. Empleados Día Requeridos Día 1 = Lunes
17 Día 2 = Martes 13 Día 3 = Miércoles 15
Día 4 = Jueves 18 Día 5 = Viernes 14 X2 :
Trabajarán martes, miércoles, jueves, viernes y
sábado y descansarán domingo y lunes. X3 :
Trabajarán miércoles, jueves, viernes,
sábado y domingo y descansarán lunes y martes. X4 :
Trabajarán jueves, viernes, sábado, domingo y lunes
y descansarán martes y miércoles. X5 :
Trabajarán viernes, sábado, domingo, lunes y martes
y descansarán miércoles y jueves. X6 :
Trabajarán sábado, domingo, lunes, martes y
miércoles y descansarán jueves y viernes. X7 :
Trabajarán domingo, lunes, martes, miércoles y
jueves y descansarán viernes y sábado. Día 6
= Sábado Día 7 = Domingo 16 Para visualizar mejor
la situación planteada y las variables que vamos a
utilizar se puede fabricar una tabla donde se indiquen los
días Los reglamentos sindicales señalan que cada
empleado de tiempo completo tiene que trabajar durante cinco
días consecutivos, y después descansar dos
días. Por ejemplo, un que trabaja cada equipo y ver la
relación existente entre ellos (coincidencia de equipos
por día de trabajo en la semana) : empleado que trabaja de
lunes a viernes, tiene que descansar el sábado y el
domingo. La oficina de correos quiere cumplir con sus
requerimientos diarios y utilizar solamente empleados de tiempo
completo. Solución : Atendiendo los reglamentos sindicales
se pueden formar equipos de trabajo bajo las siguientes
condiciones : X1 X2 X3 X4 X5 X6 X7 Empleados Requeridos Lun. 1 1
1 1 1 17 Mar. 1 1 1 1 1 13 Mié. 1 1 1 1 1 15 Jue. 1 1 1 1
1 18 Vie. 1 1 1 1 1 14 Sáb. 1 1 1 1 1 16 Dom. 1 1 1 1 1 11
X1 : Trabajarán lunes, martes, miércoles, jueves y
viernes y descansarán sábado y domingo. EJERCICIOS
RESUELTOS DE PROGRAMACION LINEAL (3era parte) Ahora se pueden
identificar las variables de decisión o incógnitas
como : Ing. José Luis Albornoz Salazar ( – 1 – )

X1LUN ; Miembros del equipo 1 que trabajan el lunes X1MAR ;
Miembros del equipo 1 que trabajan el martes X1MIE ; Miembros del
equipo 1 que trabajan el miércoles X1JUE ; Miembros del
equipo 1 que trabajan el jueves X1VIE ; Miembros del equipo 1 que
trabajan el viernes X2MAR ; Miembros del equipo 2 que trabajan el
martes X2MIE ; Miembros del equipo 2 que trabajan el
miércoles X2JUE ; Miembros del equipo 2 que trabajan el
jueves X2VIE ; Miembros del equipo 2 que trabajan el viernes
X2SAB ; Miembros del equipo 2 que trabajan el sábado X3MIE
; Miembros del equipo 3 que trabajan el miércoles X3JUE ;
Miembros del equipo 3 que trabajan el jueves X3VIE ; Miembros del
equipo 3 que trabajan el viernes X3SAB ; Miembros del equipo 3
que trabajan el sábado X3DOM ; Miembros del equipo 3 que
trabajan el domingo X4JUE ; Miembros del equipo 4 que trabajan el
jueves X4VIE ; Miembros del equipo 4 que trabajan el viernes
X4SAB ; Miembros del equipo 4 que trabajan el sábado X4DOM
; Miembros del equipo 4 que trabajan el domingo X4LUN ; Miembros
del equipo 4 que trabajan el lunes X5VIE ; Miembros del equipo 5
que trabajan el viernes X5SAB ; Miembros del equipo 5 que
trabajan el sábado X5DOM ; Miembros del equipo 5 que
trabajan el domingo X5LUN ; Miembros del equipo 5 que trabajan el
lunes X5MAR ; Miembros del equipo 5 que trabajan el martes
EJERCICIOS RESUELTOS DE PROGRAMACION LINEAL (3era parte) X6SAB ;
Miembros del equipo 6 que trabajan el sábado X6DOM ;
Miembros del equipo 6 que trabajan el domingo X6LUN ; Miembros
del equipo 6 que trabajan el lunes X6MAR ; Miembros del equipo 6
que trabajan el martes X6MIE ; Miembros del equipo 6 que trabajan
el miércoles X7DOM ; Miembros del equipo 7 que trabajan el
domingo X7LUN ; Miembros del equipo 7 que trabajan el lunes X7MAR
; Miembros del equipo 7 que trabajan el martes X7MIE ; Miembros
del equipo 7 que trabajan el miércoles X7JUE ; Miembros
del equipo 7 que trabajan el jueves Identificadas las variables
ya podemos elaborar el Modelo matemático de
Programación Lineal : Función Objetivo : MINIMIZAR
Z = X1+ X2 + X3 + X4+ X5 + X6 + X7 Restricciones : Tomando en
cuenta los empleados requeridos cada día y observando la
tabla que construimos : 1) X1LUN + X4LUN + X5LUN + X6LUN + X7LUN
2) X1MAR + X2MAR + X5MAR + X6MAR + X7MAR 3) X1MIE + X2MIE + X3MIE
+ X6MIE + X7MIE 4) X1JUE + X2JUE + X3JUE + X4JUE + X7JUE 5) X1VIE
+ X2VIE + X3VIE + X4VIE + X5VIE 6) X2SAB + X3SAB + X4SAB + X5SAB
+ X6SAB 7) X3DOM + X4DOM + X5DOM + X6DOM+ X7DOM Ing. José
Luis Albornoz Salazar ( – 2 – )

8) 9) 10) 11) 12) 13) 14) Como cada equipo debe tener la misma
cantidad de miembros trabajando cada uno de los 5 días
continuos : X1LUN = X1MAR = X1MIE = X1JUE = X1VIE X2MAR = X2MIE =
X2JUE = X2VIE = X2SAB X3MIE = X3JUE = X3VIE = X3SAB = X3DOM X4JUE
= X4VIE = X4SAB = X4DOM = X4LUN X5VIE = X5SAB = X5DOM = X5LUN =
X5MAR X6SAB = X6DOM = X6LUN = X6MAR = X6MIE X7DOM = X7LUN = X7MAR
= X7MIE = X7JUE Cuando un problema de programación lineal
tiene tantas incógnitas es recomendable solucionarlo en
EXCEL utilizando la “tabla” del método de
transporte : Los resultados se leen : 1) Se contratarán 6
empleados para el equipo 1 2) Se contratarán 5 empleados
para el equipo 2 3) Se contratarán 7 empleados para el
equipo 4 4) Se contratarán 4 empleados para el equipo 6 En
total se contratarán 22 empleados. Sea muy cuidadoso
cuando analice los resultados que arroja EXCEL, en este caso en
particular el resultado de la función objetivo refleja un
valor de 110 empleados; en realidad se refiere al total de
empleados que laboran tomando en cuenta el subtotal diario de
ellos. Si tomamos en cuenta que cada empleado trabaja 5
días a la semana, es lógico inferir que el total a
contratar EJERCICIOS RESUELTOS DE PROGRAMACION LINEAL (3era
parte) Ing. José Luis Albornoz Salazar ( – 3 – )

25 34 67 50 117 134 50 EJERCICIO 27 : El Sheraton opera los 7
días de la semana. Las mucamas son contratadas para
trabajar 6 horas diarias. El contrato colectivo especifica que
cada mucama debe trabajar 5 días consecutivos y descansar
2. Todas las mucamas reciben el mismo sueldo semanal. El Sheraton
requiere como Para determinar cuántas mucamas se necesitan
cada día se dividen las horas de servicio necesarias entre
las 6 horas de trabajo diario de cada mucama : Por tratarse de
personas, se trabajará con números enteros y se
aproximará por exceso. mínimo las siguientes horas
de servicio: lunes 150, martes 200, miércoles 400, jueves
300, viernes 700, sábado 800 y domingo 300. El
administrador desea encontrar un plan de programación de
empleos que satisfaga estos requerimientos y a un costo
mínimo. Solución : Día Lunes Martes
Miércoles Jueves Viernes Sábado Domingo Horas de
servicio Requeridas 150 200 400 300 700 800 300 Mucamas
Requeridas 25 33,33 66,67 50 116,67 133,33 50 Atendiendo lo
contemplado en el contrato colectivo se pueden formar equipos de
trabajo bajo las siguientes condiciones : X1 : Trabajarán
lunes, martes, miércoles, jueves y viernes y
descansarán sábado y domingo. X2 :
Trabajarán martes, miércoles, jueves, viernes y
sábado y descansarán domingo y lunes. X3 :
Trabajarán miércoles, jueves, viernes,
sábado y domingo y descansarán lunes y martes. X4 :
Trabajarán jueves, viernes, sábado, domingo y lunes
y descansarán martes y miércoles. X5 :
Trabajarán viernes, sábado, domingo, lunes y martes
y descansarán miércoles y jueves. X6 :
Trabajarán sábado, domingo, lunes, martes y
miércoles y descansarán jueves y viernes. X7 :
Trabajarán domingo, lunes, martes, miércoles y
jueves y descansarán viernes y sábado. EJERCICIOS
RESUELTOS DE PROGRAMACION LINEAL (3era parte) Para visualizar
mejor la situación planteada y las variables que vamos a
utilizar se puede fabricar una tabla donde se indiquen los
días que trabaja cada equipo y ver la relación
existente entre ellos (coincidencia de equipos por día de
trabajo en la semana) : Lun. Mar. Mié. Jue. Vie.
Sáb. Dom. X1 1 1 1 1 1 X2 1 1 1 1 1 X3 1 1 1 1 1 X4 1 1 1
1 1 X5 1 1 1 1 1 X6 1 1 1 1 1 X7 1 1 1 1 1 Mucamas Requeridas
Ahora se pueden identificar las variables de decisión o
incógnitas como : Ing. José Luis Albornoz Salazar (
– 4 – )

X1LUN ; Miembros del equipo 1 que trabajan el lunes X1MAR ;
Miembros del equipo 1 que trabajan el martes X1MIE ; Miembros del
equipo 1 que trabajan el miércoles X1JUE ; Miembros del
equipo 1 que trabajan el jueves X1VIE ; Miembros del equipo 1 que
trabajan el viernes X2MAR ; Miembros del equipo 2 que trabajan el
martes X2MIE ; Miembros del equipo 2 que trabajan el
miércoles X2JUE ; Miembros del equipo 2 que trabajan el
jueves X2VIE ; Miembros del equipo 2 que trabajan el viernes
X2SAB ; Miembros del equipo 2 que trabajan el sábado X3MIE
; Miembros del equipo 3 que trabajan el miércoles X3JUE ;
Miembros del equipo 3 que trabajan el jueves X3VIE ; Miembros del
equipo 3 que trabajan el viernes X3SAB ; Miembros del equipo 3
que trabajan el sábado X3DOM ; Miembros del equipo 3 que
trabajan el domingo X4JUE ; Miembros del equipo 4 que trabajan el
jueves X4VIE ; Miembros del equipo 4 que trabajan el viernes
X4SAB ; Miembros del equipo 4 que trabajan el sábado X4DOM
; Miembros del equipo 4 que trabajan el domingo X4LUN ; Miembros
del equipo 4 que trabajan el lunes X5VIE ; Miembros del equipo 5
que trabajan el viernes X5SAB ; Miembros del equipo 5 que
trabajan el sábado X5DOM ; Miembros del equipo 5 que
trabajan el domingo X5LUN ; Miembros del equipo 5 que trabajan el
lunes X5MAR ; Miembros del equipo 5 que trabajan el martes
EJERCICIOS RESUELTOS DE PROGRAMACION LINEAL (3era parte) X6SAB ;
Miembros del equipo 6 que trabajan el sábado X6DOM ;
Miembros del equipo 6 que trabajan el domingo X6LUN ; Miembros
del equipo 6 que trabajan el lunes X6MAR ; Miembros del equipo 6
que trabajan el martes X6MIE ; Miembros del equipo 6 que trabajan
el miércoles X7DOM ; Miembros del equipo 7 que trabajan el
domingo X7LUN ; Miembros del equipo 7 que trabajan el lunes X7MAR
; Miembros del equipo 7 que trabajan el martes X7MIE ; Miembros
del equipo 7 que trabajan el miércoles X7JUE ; Miembros
del equipo 7 que trabajan el jueves Identificadas las variables
ya podemos elaborar el Modelo matemático de
Programación Lineal : Función Objetivo : MINIMIZAR
) Z = X1+ X2 + X3 + X4+ X5 + X6 + X7 Restricciones : Tomando en
cuenta los empleados requeridos cada día y observando la
tabla que construimos : 1) X1LUN + X4LUN + X5LUN + X6LUN + X7LUN
2) X1MAR + X2MAR + X5MAR + X6MAR + X7MAR 3) X1MIE + X2MIE + X3MIE
+ X6MIE + X7MIE 4) X1JUE + X2JUE + X3JUE + X4JUE + X7JUE 5) X1VIE
+ X2VIE + X3VIE + X4VIE + X5VIE 6) X2SAB + X3SAB + X4SAB + X5SAB
+ X6SAB 7) X3DOM + X4DOM + X5DOM + X6DOM+ X7DOM Ing. José
Luis Albornoz Salazar ( – 5 – )

8) 9) 10) 11) 12) 13) 14) Como cada equipo debe tener la misma
cantidad de miembros trabajando cada uno de los 5 días
continuos : X1LUN = X1MAR = X1MIE = X1JUE = X1VIE X2MAR = X2MIE =
X2JUE = X2VIE = X2SAB X3MIE = X3JUE = X3VIE = X3SAB = X3DOM X4JUE
= X4VIE = X4SAB = X4DOM = X4LUN X5VIE = X5SAB = X5DOM = X5LUN =
X5MAR X6SAB = X6DOM = X6LUN = X6MAR = X6MIE X7DOM = X7LUN = X7MAR
= X7MIE = X7JUE Cuando un problema de programación lineal
tiene tantas incógnitas es recomendable solucionarlo en
EXCEL utilizando la “tabla” del método de
transporte : Los resultados se leen : 1) Se contratarán 67
mucamas para el equipo 3 2) Se contratarán 67 mucamas para
el equipo 5 En total se contratarán 134 mucamas. Sea muy
cuidadoso cuando analice los resultados que arroja EXCEL, en este
caso en particular el resultado de la función objetivo
refleja un valor de 670 mucamas; en realidad se refiere al total
de mucamas que laboran tomando en cuenta el subtotal diario de
ellas. Si tomamos en cuenta que cada mucama trabaja 5 días
a la semana, es lógico inferir que el total a contratar
EJERCICIOS RESUELTOS DE PROGRAMACION LINEAL (3era parte) Ing.
José Luis Albornoz Salazar ( – 6 – )

? ? ? ? ? ? ? ? EJERCICIO 28 : Una firma comercial fabrica dos
Solución : tipos de mermelada. Para la mermelada de fresa
utiliza la fruta y el azúcar en proporciones 2 a 3, y para
la mermelada de manzana la proporción es de 1 a 1. Se
dispone de 1000 kg de fresas, de 1500 kg de manzanas y de 3000 kg
de azúcar. La mermelada se elabora en una caldera y
posteriormente es envasada, disponiendo para ello de dos calderas
y de dos envasadoras. Las horas necesarias para fabricar 1 kg de
mermelada son: Sea muy cuidadoso a la hora de identificar las
incógnitas o variables de decisión. El
“estudiante apresurado” puede erróneamente
decir que serán dos variables : 1) Cantidad de kilogramos
de mermelada de fresa a producir y 2) Cantidad de kilogramos de
mermelada de manzana a producir. Sin embargo, al leer
detenidamente el problema podemos inferir que las mermeladas
pueden fabricarse de varias maneras y a diferentes Mermelada de
Fresa Mermelada de Manzana costos al poder utilizar la
combinación de 2 calderas y 2 envasadoras, luego las
incógnitas serán : Caldera A Caldera B Envasadora A
Envasadora B 0,6 0,9 0,01 0,04 0,9 0,9 0,02 0,03 FAA : Cantidad
de kilogramos de mermelada de fresa elaborada en la caldera
“A” y la envasadora “A”. FAB : Cantidad
de kilogramos de mermelada de fresa elaborada en la caldera
“A” y la envasadora “B”. FBA : Cantidad
de kilogramos de mermelada de fresa El número total de
horas disponibles así como el coste de su uso por hora
son: elaborada en la caldera “B” y la envasadora
“A”. FBB : Cantidad de kilogramos de mermelada de
fresa elaborada en la caldera “B” y la envasadora
“B”. MAA : Cantidad de kilogramos de mermelada de
manzana Caldera A Caldera B Envasadora A Envasadora B Horas
disponibles 1.000 5.000 100 50 Coste por hora (€) 8 4 90 40
elaborada en la caldera “A” y la envasadora
“A”. MAB : Cantidad de kilogramos de mermelada de
manzana elaborada en la caldera “A” y la envasadora
“B”. MBA : Cantidad de kilogramos de mermelada de
manzana elaborada en la caldera “B” y la envasadora
“A”. MBB : Cantidad de kilogramos de mermelada de
manzana elaborada en la caldera “B” y la envasadora
“B”. Si el precio de venta es de 15€ por kg de
mermelada de fresa y de 12€ por kg de mermelada de manzana,
¿qué cantidades de los dos tipos de mermelada se
han de producir para que se maximice el beneficio de la firma?
EJERCICIOS RESUELTOS DE PROGRAMACION LINEAL (3era parte)
Conocidas las variables es necesario determinar los costos de
cada una de ellas para poder calcular la utilidad de las mismas y
poder utilizar dichos datos en la función objetivo (Se
pide maximizar utilidad o beneficio = precio de venta menos
costos). Generalmente en estos costos se incluye el precio de
adquisición de cada kilo de fresa y cada kilo de manzana
(En este problema no se suministran estos datos) Ing. José
Luis Albornoz Salazar ( – 7 – )

Cálculo de los costos de producir cada tipo de mermelada :
Los Costos estarán representados por el tiempo utilizado
en la caldera multiplicado por el costo de su uso más el
tiempo utilizado en la envasadora multiplicado por el costo de su
uso. FAA : Cantidad de kilogramos de mermelada de fresa elaborada
en la caldera “A” y la envasadora “A”.
(0.6).(8) + (0,01).(90) = 4,8 + 0,9 = 5,7 FAB : Cantidad de
kilogramos de mermelada de fresa elaborada en la caldera
“A” y la envasadora “B”. (0,6).(8) +
(0,04).(40) = 4,8 + 1,6 = 6,4 FBA : Cantidad de kilogramos de
mermelada de fresa elaborada en la caldera “B” y la
envasadora “A”. (0,9).(4) + (0,01).(90) = 3,6 + 0,9 =
4,5 FBB : Cantidad de kilogramos de mermelada de fresa elaborada
en la caldera “B” y la envasadora “B”.
(0,9).(4) + (0,04).(40) = 3,6 + 1.6 = 5,2 MAA : Cantidad de
kilogramos de mermelada de manzana elaborada en la caldera
“A” y la envasadora “A”. (0,9).(8) +
(0,02).(90) = 7,2 + 1,8 = 9 MAB : Cantidad de kilogramos de
mermelada de manzana elaborada en la caldera “A” y la
envasadora “B”. (0,9).(8) + (0,03).(40) = 7,2 + 1,2 =
8,4 MBA : Cantidad de kilogramos de mermelada de manzana
elaborada en la caldera “B” y la envasadora
“A”. (0,9).(4) + (0,02).(90) = 3,6 + 1,8 = 5,4 MBB :
Cantidad de kilogramos de mermelada de manzana elaborada en la
caldera “B” y la envasadora “B”.
(0,9).(4) + (0,03).(40) = 3,6 + 1,2 = 4,8 EJERCICIOS RESUELTOS DE
PROGRAMACION LINEAL (3era parte) Cálculo del beneficio de
cada tipo de mermelada : FAA : Precio de venta – costos =
15 – 5,7 = 9,3 FAB : Precio de venta – costos = 15
– 6,4 = 8,6 FBA : Precio de venta – costos = 15
– 4,5 = 10,5 FBB : Precio de venta – costos = 15
– 5,2 = 9,8 MAA : Precio de venta – costos = 12
– 9 = 3 MAB : Precio de venta – costos = 12 –
8,4 = 3,6 MBA : Precio de venta – costos = 12 – 5,4 =
6,6 MBB : Precio de venta – costos = 12 – 4,8 = 7,2
La función objetivo quedará expresada como :
MAXIMIZAR Z = 9,3 FAA + 8,6 FAB + 10,5 FBA + 9,8 FBB + 3 MAA +
3,6 MAB + 6,6 MBA + 7,2 MBB Conocidos todos estos elementos es
recomendable construir una tabla donde se muestren todos los
datos del problema: Para evitar errores es bueno analizar la
información relacionada a las proporciones de la
preparación de cada mermelada : “Para la mermelada
de fresa utiliza la fruta y el azúcar en proporciones 2 a
3, y para la mermelada de manzana la proporción es de 1 a
1” De la información anterior se deduce que cada Kg.
de mermelada de fresa contiene kg. de fresa y kg. de
azúcar (0,4 Kg. de fresa y 0,6 kg. de azúcar). De
la información anterior se deduce que cada Kg. de
mermelada de manzana contiene kg. de manzana y kg. de
azúcar (0,5 Kg. de manzana y 0,5 kg. de azúcar).
Ing. José Luis Albornoz Salazar ( – 8 – )

? ? ? ? Se deben fabricar 1666,7 kilogramos de mermelada de
manzana utilizando la Caldera “B” y la Envasadora
“B” La venta de estos productos generará un
beneficio máximo de 47.050,00 € Una vez construida la
tabla anterior resulta extremadamente fácil indicar las
restricciones (prácticamente la tabla y las restricciones
poseen la misma estructura). Restricciones : 1) 0,4 FAA + 0,4 FAB
+ 0,4 FBA + 0,4 FBB = 1000 2) 0,5 MAA + 0,5 MAB + 0,5 MBA + 0,5
MBB = 1500 3) 0,6 FAA + 0,6 FAB + 0,6 FBA + 0,6 FBB + 0,5 MAA +
0,5 MAB + 0,5 MBA + 0,5 MBB = 3000 4) 0,6 FAA + 0,6 FAB + 0,9 MAA
+ 0,9 MAB = 1000 5) 0,9 FBA + 0,9 FBB + 0,9 MBA + 0,9 MBB = 5000
6) 0,01 FAA + 0,01 FBA + 0,02 MAA + 0,02 MBA = 100 7) 0,04 FAB +
0,04 FBB + 0,03 MAB + 0,03 MBB = 50 Los resultados se leen : Se
deben fabricar 2500 kilogramos de mermelada de fresa utilizando
la Caldera “B” y la Envasadora “A” Se
deben fabricar 1333,3 kilogramos de mermelada de manzana
utilizando la Caldera “B” y la Envasadora
“A” EJERCICIOS RESUELTOS DE PROGRAMACION LINEAL (3era
parte) Ing. José Luis Albornoz Salazar ( – 9 – )

= = = = – EJERCICIO 29 : En una empresa se está
discutiendo la composición de un comité para
negociar los 3) Al menos un 40% del comité serán
sindicalistas sueldos con la dirección. En el
comité habrá sindicalistas e independientes. El
número total de miembros no deberá ser inferior a
10 ni superior a 20. Al menos un 40% del comité
serán sindicalistas. El número de independientes
será como S = 40% (S + i) S = 0,40 S + 0,40 i = S = 0,40
(S + i) S – 0,40 S – 0,40 i = 0 poco una cuarta parte del
de sindicalistas. a. ¿Qué combinaciones de miembros
de cada tipo puede tener el comité?. Plantea el problema y
representa gráficamente el conjunto de soluciones.
¿Puede haber 4 sindicalistas y 16 independientes?. 0,60 S
– 0,40 i = 0 4) El número de independientes
será como poco una cuarta parte del de sindicalistas. i =
S = 4 i = S b. Si se quiere que el número de
independientes sea el mayor posible, ¿cuál
será la composición del comité?
Solución: Se definen las incógnitas o variables de
decisión : S = Cantidad de sindicalistas que
conformarán el comité. i = Cantidad de
independientes que conformarán el comité. La
función objetivo quedará definida como : Z=S+i
Restricciones : 1) El número total de miembros no
deberá ser inferior a 10 S + i = 10 2) El número
total de miembros no deberá ser superior a 20 S + 1 = 20
EJERCICIOS RESUELTOS DE PROGRAMACION LINEAL (3era parte) 4i – S =
0 Con esta información se construye la gráfica
donde se pueda visualizar el área factible de soluciones
(se recomienda leer la guía adjunta “COMO GRAFICAR
LA DESIGUALDAD”) Ing. José Luis Albornoz Salazar ( –
10 – )

; ; La zona sombreada representará el “área
factible de soluciones”, en ella se encontrarán
todos aquellos pares ordenados que cumplen simultáneamente
con TODAS las cuatro restricciones. Este par ordenado (S,i)
indicará en su parte izquierda los miembros sindicalistas
(S) que conformarán el comité y en su parte derecha
(i) los miembros independientes. En relación a uno de los
aspectos contenidos en la pregunta “a” : Al observar
el par ordenado (4,16) notamos que está ubicado arriba y a
la izquierda de la recta (3). Esta recta representa “la
frontera” de la restricción tres (0,60 S –
0,40 i = 0 ). Dicha restricción nos indica que los pares
ordenados que cumplen con ella estarán contenidas en la
recta (3) ó a la derecha y debajo de la misma. Si
sustituímos los valores (S=4 , i=16) en la
restricción 3 obtendremos : ¿Puede haber 4
sindicalistas y 16 independientes?. Se recomienda ubicar el par
ordenado en la gráfica y ver si está ubicado o
(0,60).(4) – (0,40).(16)i = 0 2,4 – 6,4 = 0 –4
= 0 no en el área sombreada. Cómo – 4 NO es
mayor ni igual a cero se afirma que el par ordenado (4,16) no
cumple con la restricción (3) y por lo tanto el
comité no puede estar conformado por 4 sindicalista y 16
independientes. b. Si se quiere que el número de
independientes sea el mayor posible, ¿cuál
será la composición del comité? El valor
más alto que puede tener la variable “i” en el
área factible de solución estará
representado por la intersección de las rectas (2) y (3)
Se puede visualizar fácilmente que el par ordenado (4,16)
está fuera del área factible de solución,
podemos afirmar que el comité no puede estar conformado
por 4 sindicalista y 16 independientes. Para confirmar lo
expresado anteriormente daremos una breve explicación para
que nuestros estudiantes tengan una visión más
clara de los conceptos estudiados. EJERCICIOS RESUELTOS DE
PROGRAMACION LINEAL (3era parte) Ing. José Luis Albornoz
Salazar ( – 11 – )

Yn Ye Ys Cn = = = = Luego para calcular dicho par ordenado se
construye un sistema con las ecuaciones (2) y (3). Formule el
problema como programación lineal y determine el programa
óptimo de producción para cada herramienta. S + i =
20 0,60 S – 0,40 i = 0 Que al ser resuelto arroja los
siguientes resultados : S = 8 ; i = 12 (8,12) Lo que nos indica
que el mayor número de miembros independientes se
logrará cuando el comité esté conformado por
20 miembros; 8 sindicalistas y 12 independientes (8,12).
Solución : Se definen las variables de decisión :
Cantidad de llaves producidas en tiempo normal. Cantidad de
llaves producidas en tiempo extra. Cantidad de llaves
subcontratadas. Cantidad de cinceles producidos en tiempo normal.
Ce Cs = = Cantidad de cinceles producidos en tiempo extra.
Cantidad de cinceles subcontratados. EJERCICIO 30 : La empresa
“SURTIDORA” contrató a EL MARTILLO como
proveedor de llaves y cinceles en sus tiendas de artículos
automotrices. La demanda semanal de Surtidora consiste en al
menos 1.500 llaves y 1.200 cinceles. La capacidad actual de
“El Martillo”, en un turno, no basta para producir
las unidades que se le piden, y debe recurrir a tiempo extra y,
quizás, a subcontratar en otros proveedores de
herramientas. El resultado es un aumento en el costo de
producción por unidad, como se ve en la siguiente tabla.
La demanda del mercado limita la producción de cinceles a
llaves a un mínimo de 2 : 1. Para definir la
función objetivo debo tomar en cuenta el costo unitario de
cada variable de decisión. MINIMIZAR Z = 2 Yn + 2,8 Ye + 3
Ys + 2,1 Cn + 3,2 Ce + 4,2 Cs Sujeta a las siguientes
restricciones : a) Demanda semanal : La demanda semanal consiste
en al menos 1500 llaves Restricción 1 : Yn + Ye + Ys =
1.500 La demanda semanal consiste en al menos 1200 Cinceles
Restricción 2 : Cn + Ce + Cs = 1.200 b) Producción
semanal : EJERCICIOS RESUELTOS DE PROGRAMACION LINEAL (3era
parte) Ing. José Luis Albornoz Salazar ( – 12 – )

? ? ? ? ? ? Los resultados se leen : Restricción 3 :
Restricción 4 : Restricción 5 : Restricción
6 : Yn = 550 Yn + Ye = 800 Cn = 620 Cn + Ce = 900 Se
fabricarán 550 llaves en tiempo normal (Yn) Se
fabricarán 250 llaves en tiempo extra (Ye) Se
subcontratarán 700 llaves (Ys) Se fabricarán 620
cinceles en tiempo normal (Cn) Se fabricarán 280 cinceles
en tiempo extra (Ce) Se subcontratarán 2100 cinceles (Cs)
c) La demanda del mercado limita la proporción de cinceles
a llaves a un mínimo de 2:1. Esta expresión una vez
simplificada quedará conformada como : Restricción
7 : Solución usando EXCEL EJERCICIOS RESUELTOS DE
PROGRAMACION LINEAL (3era parte) El costo total mínimo
para cumplir con este programa óptimo de producción
es de $ 14.918,00 EJERCICIO 31 : La empresa ESETEC SAC se dedica
a la fabricación de dos tipos de productos A y B, en la
que utiliza los insumos X y Y. Para la elaboración del
producto A se necesita 01 unidad del insumo X y una unidad del
insumo Y; para el producto B se necesita 03 unidades del Insumo X
y 01 del insumo Y. Los informes de los proveedores indican que se
debe adquirir como mínimo 600 unidades del insumo X y 400
del insumo Y. El taller puede fabricar 1000 unidades del Producto
A o 1200 del producto B, o cualquier combinación de estos.
El área de acabado tiene disponible 5.600 minutos, de los
que cada unidad del producto A utiliza 04 minutos y cada unidad
de producto B consume 07 minutos. El área de ventas
informa que pueden vender cualquier cantidad del producto A; sin
embargo, del producto B a lo máximo se pueden vender 600
unidades. Los costos variables de producción son de $.
24.00 para el producto A y $.16.00 para el producto B.
¿Cuál es la forma más productiva para
fabricar estos productos, si sabemos que los precios de venta son
$ 32.00 y $ 23.00 del producto A y B respectivamente? Indique: 1)
Cantidad óptima que se debe producir de A y B. y 2)
Ganancia máxima. Ing. José Luis Albornoz Salazar (
– 13 – )

A 4 B 7 A 1 B 3 Solución : El taller puede fabricar 1200
unidades del producto “B” Se definen las variables
como : Restricción 4 : B = 1200 A = Cantidad de productos
“A” a producir. B = Cantidad de productos
“B” a producir. Para definir la función
objetivo es necesario conocer la utilidad de cada producto, para
lo cual debemos recordad que : Utilidad = Precio de venta menos
costo de producción. O cualquier combinación de
estos Restricción 5 : Para simplificar la expresión
anterior podemos utilizar como mínimo común
múltiplo a 1200 y la restricción quedará
indicada como Utilidad de A = 32,00 – 24,00 = $ 8,00
Utilidad de B = 23,00 –16,00 = $ 7.00 Restricción 5
: 1,2 A + B = 1200 Luego, Z = 8A + 7B c) Area de acabados :
Estudiando las restricciones : a) Utilización de insumos :
Minutos utilizados Restricción 6 : Minutos disponibles
5600 4A + 7B = 5600 Insumo X Adquirir como mínimo 600 d)
Area de ventas : Insumo Y 1 1 400 Pueden vender cualquier
cantidad del producto A Restricción 1 : Restricción
2 : 1A + 3B = 600 1A + 1B = 400 Restricción 7 : A = 0 Del
producto B a lo máximo se pueden vender 600 unidades. b)
Capacidad de producción : Restricción 8 : B = 600
El taller puede fabricar 1000 unidades del producto
“A” Utilizando la hoja de cálculo Excel y
aplicando SOLVER el Restricción 3 : A = 1000 resultado
será : EJERCICIOS RESUELTOS DE PROGRAMACION LINEAL (3era
parte) Ing. José Luis Albornoz Salazar ( – 14 – )

EJERCICIO 32 : Tres sustancias X, Y y W contienen cuatro
ingredientes A, B, C y D. En la siguiente tabla están
dados los porcentajes de cada ingrediente y el costo por onza (en
centavos de dólar) de las tres sustancias: Sustancia X Y W
A 20% 20% 10% B 10% 40% 20% C 25% 15% 25% D 45% 25% 45%
Costo/Onza 25 35 50 1) ¿ Cuántas onzas se deben
combinar de cada sustancia para obtener, con un costo
mínimo, 20 onzas de la mezcla con un contenido de al
menos.14% de A. 16% de B y 20% de C ? Tomando en cuenta que los
resultados deben ser enteros por tratarse de “unidades de
producto”, el resultado será : Se deberán
producir 636 productos “A” y 436 productos
“B” y se obtendrá una ganancia máxima
de $ 8.140,00 EJERCICIOS RESUELTOS DE PROGRAMACION LINEAL (3era
parte) 2) ¿Con cuántas se maximiza? SOLUCIÓN
: Definición de Variables : X = Cantidad de onzas de la
sustancia “X” que se debe mezclar. Y = Cantidad de
onzas de la sustancia “Y” que se debe mezclar. W =
Cantidad de onzas de la sustancia “W” que se debe
mezclar. Función Objetivo : Z = 25 X + 35 Y + 50 W
Restricciones : 1) Se deben obtener 20 onzas de la mezcla : Esto
nos obliga a inferir que la suma de las tres sustancias debe ser
igual a 20. X + Y + W = 20 Ing. José Luis Albornoz Salazar
( – 15 – )

2) La mezcla debe contener al menos 14% de “A” : El
14% de las 20 onzas = (0,14)*(20) = 2,80 0,20 X + 0,20 Y + 0,10 W
= 2,80 3) La mezcla debe contener al menos 16% de “B”
: El 16% de las 20 onzas = (0,16)*(20) = 3,20 0,10 X + 0,40 Y +
0,20 W = 3,20 4) La mezcla debe contener al menos 20% de
“C” : El 20% de las 20 onzas = (0,20)*(20) = 4,00
0,25 X + 0,15 Y + 0,25 W = 4,00 Nota : No se toman en cuenta los
valores del ingrediente “D” porqué no tiene
limitación alguna. MINIMIZACIÓN :
MAXIMIZACIÓN : EJERCICIO 33 : A un joven matemático
se le pidió que entreviste a un visitante en su empresa
durante tres horas, el pensó que sería una
excelente idea que el huésped se emborrachara. Se le
dieron al matemático 50 dólares para comprar la
bebida. El joven sabía que al visitante le gustaba mezclar
sus tragos pero que siempre bebía menos de 8 vasos de
cerveza, 10 de ginebra, 12 de whiskys y 24 de martinis. El tiempo
que empleaba para beber era de 10 minutos por cada vaso. El costo
de bebidas son: $1.00 el vaso de cerveza, $2.00 el vaso de
ginebra, $4.00 el vaso de whiskys y $3.00 el vaso de martini. El
matemático pensó que el objetivo sería
maximizar el consumo alcohólico del huésped.
Logró que un amigo químico le diese el contenido
alcohólico de las bebidas en forma cuantitativa, siendo
las unidades alcohólicas de 8, 15, 16 y 7 por EJERCICIOS
RESUELTOS DE PROGRAMACION LINEAL (3era parte) Ing. José
Luis Albornoz Salazar ( – 16 – )

vaso de cerveza, ginebra, whisky y martini respectivamente. El
visitante siempre bebía un mínimo de 2 whiskys.
¿Cómo resolvió el problema el joven?
SOLUCIÓN : Definición de las variables C = Cantidad
de vasos de cerveza a servir al visitante. G = Cantidad de vasos
de ginebra a servir al visitante. W = Cantidad de vasos de whisky
a servir al visitante. M = Cantidad de vasos de martini a servir
al visitante. Función objetivo : El matemático
pensó que el objetivo seria maximizar el consumo
alcohólico del huésped. MAXIMIZAR Z = 8 C + 15 G +
16 W + 7 M Restricciones : 1) Se le dieron al matemático
50 dólares para comprar la bebida….. El costo de
bebidas son: $1.00 el vaso de cerveza, $2.00 el vaso de ginebra,
$4.00 el vaso de whiskys y $3.00 el vaso de martini. 1 C + 2 G +
4 W + 3 M = 50 2) El joven sabía que al visitante le
gustaba mezclar sus tragos pero que siempre bebía menos de
8 vasos de cerveza, 10 de ginebra, 12 de whiskys y 24 de martinis
C = 8 G = 10 W = 12 M = 24 EJERCICIOS RESUELTOS DE PROGRAMACION
LINEAL (3era parte) 3) A un joven matemático se le
pidió que entreviste a un visitante en su empresa durante
tres horas….(3 horas = 180 minutos)…. El tiempo que
empleaba para beber era de 10 minutos por cada vaso. 10 C + 10 G
+ 10 W + 10 M = 180 4) El visitante siempre bebía un
mínimo de 2 whiskys. W = 2 Los resultados se leen : El
joven matemático le ofrecerá al visitante 1 vaso de
cerveza, 10 vasos de ginebra y 7 vasos de whisky. Esto le
suministrará al visitante 270 unidades alcohólicas.
Se gastarán $ 49. El visitante pasará todos los 180
minutos (3 horas) consumiendo las bebidas alcohólicas Ing.
José Luis Albornoz Salazar ( – 17 – )

Utilidad por Nivel de Proyecto peso Clasificación del
Proyecto 3 4.1 250 EJERCICIO 34 : Una oficina federal cuenta con
un Solución presupuesto de mil millones de pesos para
otorgarlo como subsidio destinado a la investigación
innovadora en el campo de la búsqueda de otras formas de
producir energía. Un equipo gerencial integrado por
científicos y economistas efectuó una reseña
preliminar de 200 solicitudes, reduciendo los candidatos a seis
finalistas. Los seis proyectos han sido evaluados calificados en
relación con los beneficios que se espera conseguir de
ellos en los próximos 10 años. Los beneficios
estimados se dan en la siguiente tabla: financiamiento (en
invertido millones de pesos) 1 Solar 4.4 220 2 Solar 3.8 180
Combustibles sintéticos 4 Carbón 3.5 150 5 Nuclear
5.1 400 6 Geotérmico 3.2 120 Así el valor 4.4
asociado al proyecto 1, indica que por cada Definiendo las
variables : ? S1 = Cantidad de dinero que se otorgará al
proyecto 1 de energía solar (millones de pesos) ? S2 =
Cantidad de dinero que se otorgará al proyecto 2 de
energía solar (millones de pesos) ? Cs = Cantidad de
dinero que se otorgará al proyecto de Combustible
sintético (millones de pesos) ? CA = Cantidad de dinero
que se otorgará al proyecto de Carbón (millones de
pesos) ? N = Cantidad de dinero que se otorgará al
proyecto Nuclear (millones de pesos) ? G = Cantidad de dinero que
se otorgará al proyecto Geotérmico (millones de
pesos) peso que se invierta en ese proyecto, se obtendrá
una utilidad de 4.40 durante los próximos diez
años. La tabla muestra, además, Función
Objetivo : MAXIMIZAR BENEFICIOS (utilidades) el nivel requerido
de financiamiento (en millones de pesos). Esas cifras representan
la cantidad máxima de que se dispone para cada proyecto.
La oficina federal puede conceder a cada proyecto una suma que no
rebase esa cifra. Observando estas disposiciones, el presidente
ha ordenado financiar el proyecto nuclear por lo menos en el 50%
de la suma solicitada. El administrador de la dependencia
gubernamental tiene mucho interés en el proyecto solar y
ha pedido que la cantidad combinada que se conceda a estos
proyectos sea como mínimo de 300 millones de pesos. El
problema consiste en determinar las sumas de dinero que se
otorgaran a cada proyecto con objeto de maximizar los beneficios.
EJERCICIOS RESUELTOS DE PROGRAMACION LINEAL (3era parte) Z = 4,40
S1 + 3,80 S2 + 4,10 CS + 3,50 CA + 5,10 N + 3,20 G Restricciones
: 1) Una oficina federal cuenta con un presupuesto de mil
millones de pesos para otorgarlo como subsidio S1 + S2 + CS + CA
+ N + G = 1.000 2) Nivel de financiamiento : S1 = 220 Ing.
José Luis Albornoz Salazar ( – 18 – )

S2 CS CA N G = = = = = 180 250 150 400 120 Los resultados se leen
: ? S1 = Cantidad de dinero que se otorgará al proyecto 1
de energía solar (millones de pesos) = 220 3) El
presidente ha ordenado financiar el proyecto nuclear por lo menos
en el 50% de la suma solicitada (50% de 400 = 200) N = 200 4) El
administrador de la dependencia gubernamental tiene mucho
interés en el proyecto solar y ha pedido que la cantidad
combinada que se conceda a estos proyectos sea como mínimo
de 300 millones de pesos. S1 + S2 = 300 Solución en la
hoja de cálculo EXCEL : EJERCICIOS RESUELTOS DE
PROGRAMACION LINEAL (3era parte) ? S2 = Cantidad de dinero que se
otorgará al proyecto 2 de energía solar (millones
de pesos) = 130 ? Cs = Cantidad de dinero que se otorgará
al proyecto de Combustible sintético (millones de pesos) =
250 ? CA = Cantidad de dinero que se otorgará al proyecto
de Carbón (millones de pesos) = 0 ? N = Cantidad de dinero
que se otorgará al proyecto Nuclear (millones de pesos) =
400 ? G = Cantidad de dinero que se otorgará al proyecto
Geotérmico (millones de pesos) = 0 Los beneficios que se
lograrán con esta inversión asciende a : Z
máxima = 4.527 millomes de pesos Ing. José Luis
Albornoz Salazar ( – 19 – )

EJERCICIO 35 : Una compañía se dedica a la
fabricación de 4 productos : P1, P2, P3 y P4, utilizando
para ello 2 materias primas : M1 y M2, cuyas disponibilidades
semanales están limitadas a 1000 y 1200 unidades
respectivamente. La materia prima que precisa la
fabricación de una unidad de cada una unidad de cada uno
de los productos se muestra en la siguiente tabla :
Además, los costos de fabricación de cada unidad de
producto (que incluyen los costos de la materia prima y otros) se
han evaluado en 75, 60, 40 y 30 unidades monetarias
respectivamente. La próxima semana la
compañía debe atender un pedido de 100 unidades de
P1, 110 de P2, 120 de P3 y 90 de P4, lo que supera claramente su
capacidad de producción. Por esta razón,
está considerando la posibilidad de adquirir algunos de
estos productos a un competidor, cuyos productos tienen las
mismas características que los que fabrica la
compañía. Este competidor sólo puede
suministrar unidades de los productos P1, P2 y P3, y los ofrece a
85, 65 y 30 u.m. por unidad, respectivamente. Plantear un modelo
que permita determinar cuántos productos de cada tipo debe
elaborar la compañía y cuántos debe comprar
para satisfacer la demanda de este pedido de manera que se
minimicen los costos totales. Solución : Primero se
identifican las variables de decisión : P1f = Cantidad de
producto P1 a fabricar. P2f = Cantidad de producto P2 a fabricar.
EJERCICIOS RESUELTOS DE PROGRAMACION LINEAL (3era parte) P3f =
Cantidad de producto P3 a fabricar. P4f = Cantidad de producto P4
a fabricar. P1c = Cantidad de producto P1 a comprar. P2c =
Cantidad de producto P2 a comprar. P3c = Cantidad de producto P3
a comprar. La función objetivo quedará representada
por los costos de fabricación y los costos de
adquisición de las variables : MINIMIZAR Z = 75.P1f +
60.P2f + 40.P3f + 30.P4f + 85.P1c + 65.P2c + 30.P3c Restricciones
: a) Uso y disponibilidad de la materia prima M1 6.P1f + 3.P2f +
5.P3f + 4.P4f = 1000 b) Uso y disponibilidad de la materia prima
M2 4.P1f + 7.P2f + 2.P3f + 5.P4f = 1200 c) Pedidos de productos :
P1f + P1c = 100 P2f + P2c = 110 P3f + P3c = 120 P4f = 90
Solución con Excel : Ing. José Luis Albornoz
Salazar ( – 20 – )

? ? ? ? ? ? ? Los resultados se leen : P1f = Cantidad de producto
P1 a fabricar = 100 P2f = Cantidad de producto P2 a fabricar =13
P3f = Cantidad de producto P3 a fabricar = 0 P4f = Cantidad de
producto P4 a fabricar = 90 P1c = Cantidad de producto P1 a
comprar = 0 P2c = Cantidad de producto P2 a comprar = 97 P3c =
Cantidad de producto P3 a comprar = 120 Z mínima =
20.885,00 u.m. Como se trata de Unidades de Productos es
recomendable que los resultados se expresen en números
enteros, no se recomienda hacer aproximaciones, se recomienda
utilizar PROGRAMACION LINEAL ENTERA EJERCICIO 36 : Un fabricante
tendrá que atender cuatro pedidos de producción, A,
B, C, y D, en este mes. Cada trabajo puede ser llevado a cabo en
cualquiera de los tres talleres. El tiempo necesario para
completar cada trabajo en cada uno de esos talleres, el costo por
hora y la cantidad de horas disponibles que tendrá cada
taller durante este mes aparecen en la siguiente tabla.
EJERCICIOS RESUELTOS DE PROGRAMACION LINEAL (3era parte) Ing.
José Luis Albornoz Salazar ( – 21 – )

1.1.- 1.2.- 1.3.- 3.1.- 3.2.- 3.4.- También existe la
posibilidad de dividir cada uno de los trabajos entre los
distintos talleres, en cualquier proporción que se desee.
Por ejemplo, una cuarta parte del trabajo A puede hacerse en 8
horas en el taller 1. El fabricante desea determinar la cantidad
de horas de cada trabajo que deberán realizarse en cada
taller, para minimizar el costo total de terminación de
los cuatro trabajos. Identifique las variables de
decisión, formule un modelo de PL para este problema y
finalmente resuélvalo. Restricciones : 1) Tiempo
disponible en cada taller T1A + T1B + T1C + T1D = 160 T2A + T2B +
T2C + T2D = 160 T3A + T3B + T3C + T3D = 160 2) Tiempo requerido
en cada taller para cada producto : 2.1.- T1A = 32
Definición de variables T1A = Cantidad de horas en el
taller 1 para el trabajo A T1B = Cantidad de horas en el taller 1
para el trabajo B T1C = Cantidad de horas en el taller 1 para el
trabajo C T1D = Cantidad de horas en el taller 1 para el trabajo
D T2A = Cantidad de horas en el taller 2 para el trabajo A 2.2.-
2.3.- 2.4.- 2.5.- 2.6.- 2.7.- 2.8.- 2.9.- 2.10.- 2.11.- 2.12.-
T1B T1C T1D T2A T2B T2C T2D T3A T3B T3C T3D = = = = = = = = = = =
151 72 118 39 147 61 126 46 155 57 121 T2B = Cantidad de horas en
el taller 2 para el trabajo B T2C = Cantidad de horas en el
taller 2 para el trabajo C 3) Posibilidad de dividir cada uno de
los trabajos entre l
Página siguiente  |
