
?? ?? ?? ?? ?? ?? ?? ?? ?? ?? ??+1 1 ?? LA INTEGRAL DEFINIDA
Geométricamente la integración, surgió de la
necesidad de calcular áreas de superficies limitadas por
curvas. El área bajo la curva y = f(x) entre los
intervalos a y b es: Á?????? = ??? ?? ·? ?? ?
Á?????? = ??? ??(??) ·? ?? ?? Á?????? = lim
??? ??(??) ? ?? ó también Á?????? = ?
??(??)???? ????0 Por lo que si f es una función definida
en un intervalo cerrado [??, ??], la integral definida es: ?? ??
? ??(??)???? = ?????? ? ??(??) ? ?? = ??(??) – ??(??) ?????? ?? A
la expresión anterior se la conoce como Teorema
Fundamental del Cálculo LEYES BÁSICAS 1) Para c
contante ?? ? ?????? = ??(?? – ??) ?? ?? ?? ? ????(??)???? ??? ?
??(??)???? ?? ?? ?? ?? ?? 2) ? [??(??) ± ??(??)]???? = ?
??(??)???? ± ? ??(??)???? ?? ?? ?? 3) ? ??(??
)???????(??)]?? ???(??) – ??(??) ?? 4) ? ?? ????? ] ? ?? ?? + 1
?? ?? + 1 ?? ?? 5) ? ??(??)????? [? ??(??)????] (????+1 – ????+1
) ?? ??
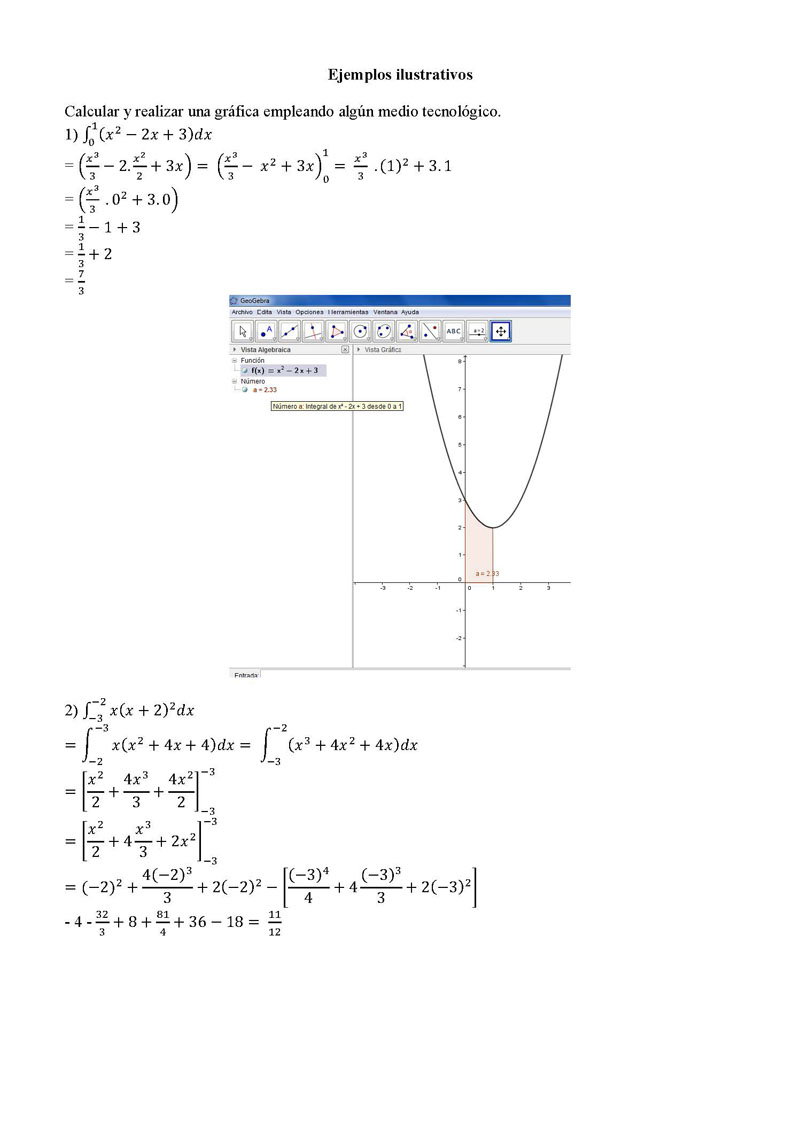
0 1 ?? 3 3 -3 =? -3 2 3 -3 2 3 2 Ejemplos ilustrativos Calcular y
realizar una gráfica empleando algún medio
tecnológico. 1 1) ? (?? 2 – 2?? + 3)???? ?? 3 ?? 2 ?? 3 =
( 3 – 2. 2 + 3??) = ( 3 – ?? 2 + 3??)0 = ?? 3 = ( 3 . 02 + 3. 0)
1 = 3 -1+3 1 = 3 +2 7 = 3 . (1)2 + 3. 1 -2 2) ? ??(?? + 2)2 ????
-3 -2 ??(?? 2 + 4?? + 4)???? = ? (?? 3 + 4?? 2 + 4??)???? -2 ?? 2
4?? 3 4?? 2 =[ + + ] 2 -3 ?? 2 ?? 3 = [ + 4 + 2?? 2 ] -3 4(-2)3 =
(-2) + +2 3 -3 (-3)4 (-2)2 – [ 4 +4 (-3)3 3 + 2(-3)2 ] 32 81 11 –
4 – 3 + 8 + 4 + 36 – 18 = 12

1 1 8 1 3 1/ 3 1 1 3 3 4 2 3 3 4 4 2 -2/ 4 2 3 2 2 4 3 4/ 5) ?
(?? 3 – ?? -3 ) ????= ? ?? 1/ ???? = ? ?? – ???? ?? /3+1 ?? –
/3+1 = ( – ) 4/ 2/ ?? /3 ?? – /3 = ( – ) 4/ 2/ = (3 ?? /3 – 3 ??
3 ) = ( (8) 3 – (8) /3 ) – ( (1) /3 – (1) /2 ) 3 3 4 3 3 3 3 3 =
. 16 – . 4 – ( . 1 – . 1) 4 2 4 2 3 3 = 12 – 6 – 4 + 2 27 =
4

?? ÁREA COMO INTEGRAL DEFINIDA Caso Nº 1 Si f es
función continua en el intervalo cerrado ?a,b? tal que
f(x) ? 0, ?x ??a,b?; el área de la región R
limitada por la curva y = f(x), el eje X y las rectas x=a y x=b,
está dado por la expresión ?? ??(??) = ? ??(??)????
Nota: Si f es función continua en el intervalo cerrado
?a,b? tal que f(x) ? 0, ?x ??a,b?; el área de la
región R limitada por la curva y = f(x), el eje X y las
rectas x=a y x=b, está dado por la expresión ??
??(??) = |? ??(??)????| ??

?? Si la región R es limitada por la curva x = g(y) y las
retas y = c, y =d, entonces el área de la región R
es expresado por: ?? ??(??) = ? ??(??)???? ?? Caso Nº 2 Si f
y g son funciones continuas en el intervalo cerrado ?a,b? tal que
f(x) ? g(x), ?x ??a,b?; el área de la región R
limitada por las curvas y = f(x), y =g(x) y las rectas x=a y x=b,
está dado por la expresión ?? ??(??) = ? (??(??) –
??(??))???? ?? Nota: Si g y h son funciones continuas en el
intervalo cerrado ?a,b? tal que g(y) ? h(y),?y ??a,b?; el
área de la región R limitada por las curvas x =
g(y) y x =h(y) y las rectas y=c , y=d, está dado por la
expresión ?? ??(??) = ? (??(??) – h(??))????

{ 2 2 ) 2 -1 Ejemplos ilustrativos Calcular el área
limitada por las siguientes funciones 1) ?? = 3 – ?? 2 ; ?? = 1 –
?? Resolviendo el sistema ?? = 3 – ?? 2 ?? = 1 – ?? Se obtiene
??1 = 2; ??2 = -1 Aplicando ?? ??(??) = ? (??(??) – ??(??))????
?? ?(3 – ?? – (1 – ??)???? = ?(3 – ?? – 1 + ??)???? = ?(?? 2 ?? 3
– ?? – 2) ???? = ( + ?? 2 – 2) 3 23 = ( 3 – 22 2 – 2) – ( -13 3 –
-12 2 8 4 1 1 8 3 – 2) = (3 – 2 – 2) – (- 3 – 2 – 2) = (3 – 2 –
2) – (-2 – 6 – 12) =( 8-12 3 17 4 ) – (- 6 ) = – 3 + 17 6 9 = 2
??2

2) ?? = ?? 3 + 3??2 + 2; ?? = ?? 3 + 6?? 2 – 25

? ? y0 m0 ? 0 x0 m0 2 5 2 2 4 5 24 8 Aplicaciones en
Administración y Economía Excedente del consumidor
Es igual a x0 0 f ( x)dx ? x0 y0 donde y ? f ( x) es la
función demanda O también es igual a g( y)dy ,
donde x ? g ( y) es la función de demanda Excedente del
Productor Es igual a x0 y0 ? f ( x)dx , donde y ? f ( x) es la
función de oferta O también es igual a x0 y0 ? ?y0
g ( y)dy , donde donde x ? g ( y) es la función de oferta
Ingreso frente a Costo La utilidad máxima se determina
igualando el ingreso marginal y el costo marginal y la ganancia
total es la integral de la diferencia entre el ingreso marginal y
el costo marginal desde cero hasta la cantidad para el cual la
utilidad es máxima Ejemplos ilustrativos 1) Si la
función de demanda es y ? 39 ? x , hallar el excedente del
consumidor si x0 ? . Realizar la gráfica respectiva
manualmente y empleando el programa Graph o cualquier otro
programa. 5 2 131 ??0 = 39 – ( ) = Excedente del consumidor ? (39
– ?? 2 )???? – ??0 ??0 = [39?? – ] – · = – 5 2 ?? 3 2 5
131 2215 655 ?? 3 0 2 4 = 10,41

2 2 3 16 3 0 32 3 2) Las funciones de demanda y oferta en un
mercado de competencia pura o libre son respectivamente y ? 14 ?
x2 y y ? 2×2 ? 2 ; determinar el excedente del consumidor y del
producto Calculando el punto de intersección entre las
funciones se considera el punto (2,10) Excedente del consumidor
?? 3 8 ? (14 – ?? 2 )???? – ??0 ??0 = [14?? – ] – 2 · 10 =
28 – – 20 = ?? 3 0 Excedente del producto 2 ??0 ??0 – ? ?? 2?? 3
(2?? 2 + 2)???? = 2 · 10 – [ 3 2 16 + 2??] = 20 – ( + 4) =
3
